Тема. Вариационный ряд и его характеристики
Понятие вариационного ряда
Пример 1. Рассмотрим в качестве изучаемого признака число продаж каждого из 26 случайно выбранных продавцов универмага:
16, 12, 15, 15, 23, 9, 15, 13, 14, 14, 21, 15, 14, 17, 27, 15, 16, 12, 16, 19, 14, 16, 17, 13, 14, 14.
Обозначив изучаемый признак латинской буквой Х, запишем в общем виде: x1, x2,..., xn (n=26), где
x1, x2,..., xn - упорядоченные значения признака, которые в статистике называются вариантами.
Варианты, расположенные в возрастающем (или убывающем) порядке т.е. ранжированные, и составляют вариационный ряд: 9, 12, 12, 13, 13, 13, 14, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 16, 16, 16, 17, 17, 19, 21, 23, 27.
Абсолютные числа, показывающие сколько раз встречаются те или иные варианты в ряду, называются частотами (весами), они обозначаются m1, m2,... mk или f1, f2,... fk, где k - число групп в вариационном ряду (k < n).
Таблица 1
Общий вид вариационного ряда
| Значения признака (хi) | x1 | x2 | ... | xk |
| Частоты (mi) | m1 | m2 | ... | mk |
k
где å mi = n
i=1
Таблица 2
Данные о числе товаров, проданных 26 продавцами универмага
| Число продаж (хi) | |||||||||||
| Число продавцов (mi) |
В полученном ряду k = 11, а n = å mi = 26
i=1
Отношение частоты того или иного варианта к сумме всех частот ряда называется частостью или относительной частотой.
wi = mi / å mi (1)
Таблица 3
Вариационный ряд частостей числа товаров, проданных 26 продавцами
| Число продаж (хi) | |||||||||||
| Доля продавцов (wi) | 0,04 | 0,08 | 0,11 | 0,23 | 0,19 | 0,11 | 0,08 | 0,04 | 0,04 | 0,04 | 0,04 |
Сумма всех частостей равна 1, т.е. å wi = 1. Частости могут быть выражены в процентах, тогда
|
|
их сумма равна 100%.
Признак называется дискретно варьируемым, если его отдельные значения (варианты) отличаются друг от друга на некоторую конечную величину (обычное целое число), вариационный ряд таких признаков называется дискретным вариационным рядом. Примеры: тарифный разряд рабочего, цена товара, число семян в 10 граммовом пакете и т.д.
Существует множество признаков, значения которых отличаются друг от друга на сколько угодно малую величину, т.е. признак может принимать любые значения в некотором интервале. Такие признаки называются непрерывно варьирующими. Например, индексы экономического состояния, среднедушевые доходы, процент дневной выработки рабочего, вес одного семени и т.п.
Данные, представленные непрерывно варьирующим признаком, представляют в виде интервального вариационного ряда.
Пример 2. Менеджер большого универмага записал суммы денег, которые израсходовали 184 покупателя, посетившие отдел верхней одежды в день сезонной распродажи по сниженным ценам. Зная минимальную и максимальную стоимость покупки, менеджер сгруппировал данные о суммах, израсходованных на покупки в следующем виде:
Таблица 4
Суммы денег, израсходованные на покупки товаров в отделе верхней одежды (тыс. руб.)
| Интервалы расходов | 100-300 | 300-500 | 500-700 | 700-900 | 900-1100 | 1100-1300 |
| Число поку-пателей (mi) | ||||||
| Доля поку-пателей (wi) | 0,163 | 0,207 | 0,272 | 0,168 | 0,120 | 0,070 |
ki = xi(max) - xi (min) (2)
x (max) - x (min)
k = ¾¾¾¾¾¾¾, (3)
1 + 3,322 lg n
Для данных примера 1: x(max)=27 x(min)=9
|
|
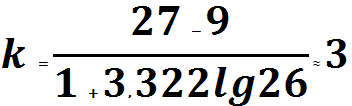
Преобразованные в интервальный ряд данные примера 1 имеют следующий вид:
| Интервалы продаж | 9-12 | 12-15 | 15-18 | 18-21 | 21-24 | 24 - 27 |
| Число продавцов (mi) |
z = 2ln n (4)
и тогда:
x (max) - x (min)
k = ¾¾¾¾¾¾¾¾ (5)
z
Для примера 1 z=2ln n=2ln26=6,5162»7
k=(27-9)/7=2,5714»3, что совпадает с результатом, полученным по формуле 3.
Средняя арифметическая - это отношение суммы произведений значений вариантов на соответствующие частоты к сумме всех частот.
(6)
(7)
где - mi - частоты вариационного ряда, wi частости, k - число групп с одинаковыми значениями признака.
Формулы 6 и 7 применяют в случае, если вариационный ряд сгруппирован по одинаковым значениям вариантов. Повторяющиеся варианты ряда умножаются («взвешиваются») на соответствующие частоты, поэтому эти формулы в статистике называют средней арифметической взвешенной.
Для расчета средней можно использовать и не взвешенные данные, тогда формула средней арифметической будет иметь вид:
(8)
= (х1 + х2 + х 3 +... + хn) / n = (9 + 12 + 12 +
+13 +13 +13 + 14 + 14 + 14 + 14 + 14 + 14 + 15 + 15 + 15 + 15 + +15 + 16 + 16 +16 +17 + 17 + 19 + 21 +23 + 27)/26 = 15,5.
По формуле средней арифметической взвешенной:
=(9.1+12.2+13.3+14.6+15.5+16.3+17.2+19.1+21.1+
23. 1+27.1)/26=15,5.
Для данных примера 2:
х = [(100 + 300)/2]. 30 + [(300 + 500)/2]. 38 +
+[(500 + 700)/2]. 50 +
+ [(700+900)/2]. 31+[(900+1100)/2)]. 22+
+[(1100+1300)/2]. 13=617,39
Мода ( Мо) - это значение признака, наиболее часто встречающеecя в вариационном ряду.
Медиана - значение признака ряда, относительно которого вариационный ряд делится на две равные по числу вариантов части.
|
|
Пусть заданы два вариационных ряда:
Ряд 1. 1 2 3 4 5 6 6 7 8 9 10 11
Ряд 2. 4 5 5 5 6 6 6 6 7 7 7 8
Рассчитаем для этих рядов средние значения, моду и медиану.
Ряд1. x = 6, Ме=6, Мо=6, n=12,
Ряд2. x = 6, Ме=6, Мо=6, n=12
В чем же разница?
Рисунок 1 графически изображает ряд I и ряд II.
Размах вариации в ряду - разность между наибольшим и наименьшим значениями признака.
R = xmax - xmin
- среднее линейное отклонение, (9),
- дисперсия, (10).
Для взвешенных вариант:
(11).
Дисперсия вариационного ряда есть средняя арифметическая квадрата отклонения (средний квадрат отклонения) значений признаков ряда от их средней арифметической.
(12)
Стандартное отклонение вариационного ряда есть арифметическое значение корня квадратного из дисперсии.
__
s = Ös2 (13)
Коэффициент вариации
(14)
или
