Тема: Угол между прямыми. Параллельность плоскостей. Тетраэдр и параллелепипед. Задачи на построение сечений.
Повторите стр.17-18
Ознакомьтесь с решением задач, перепишите или приклейте распечатку в тетрадь.
№44
| D |
| С |
| В |
| О |
| 𝛼 |
Дано: ОВ 
CD, OA и CD - скрещивающиеся прямые,
а) 
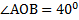; б)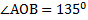 
.
Найти: угол между прямыми ОА и CD.
Решение.
Прямые ОВ CD, поэтому они лежат в некоторой плоскости 𝛼. А 
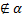, CD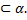 
Тогда по признаку скрещивающихся прямых OA и CD - скрещивающиеся прямые, что соответствует условию задачи.
Построим прямую через точку С прямую СЕ, параллельную ОА(А и Е лежат по одну сторону от плоскости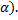 
ОВ CD, Лучи ОА и CD соноправленны, ОВ и CD соноправленны.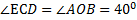 
.Тогда угол между скрещивающимися прямыми ОА и CD равен 
.
| D |
| С |
| В |
| О |
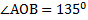, то он тупой. А углом между пересекающимися прямыми называют угол, лежащий в (0; 
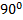].Тогда угол между прямыми ОВ и ОА равен 
.
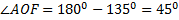5 Ho5GceTTYTR+m+PB7Wvm+xqzqs4AO2eI+8ryJEZ80L0oHVT3uGxm8VVUMcPx7YKGXjwL7V7BZcXF bJZAOOSWhUtza3l0HVmOLXzX3DNnuz4POCBX0M86mzxp9xYbLQ3MVgGkSrMQeW5Z7fjHBZGmqVtm cQPtnxPqYeVOfwMAAP//AwBQSwMEFAAGAAgAAAAhAOuTv6LfAAAACQEAAA8AAABkcnMvZG93bnJl di54bWxMj01Pg0AQhu8m/ofNmHizC5VWQJaGaIyJmhirF29TGIHIzhJ229J/73jS23w8eeeZYjPb QR1o8r1jA/EiAkVcu6bn1sDH+8NVCsoH5AYHx2TgRB425flZgXnjjvxGh21olYSwz9FAF8KYa+3r jiz6hRuJZfflJotB2qnVzYRHCbeDXkbRWlvsWS50ONJdR/X3dm8NPCWfeH8dnukUeH6tqsd0TPyL MZcXc3ULKtAc/mD41Rd1KMVp5/bceDUYSLJVJqgUN2tQAqyWqQx2BrI4Bl0W+v8H5Q8AAAD//wMA UEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5 cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3Jl bHMvLnJlbHNQSwECLQAUAAYACAAAACEAouKhqp0CAAC6BQAADgAAAAAAAAAAAAAAAAAuAgAAZHJz L2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEA65O/ot8AAAAJAQAADwAAAAAAAAAAAAAAAAD3BAAA ZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAAMGAAAAAA== " fillcolor="white [3201]" strokecolor="white [3212]" strokeweight=".5pt">
| 𝛼 |
К
| F |
| М |
Построим через точку С прямую СК, параллельную прямой FA.Точки А и К лежат по одну сторону от плоскости 𝛼.
Луси СМ и ОF соноправленны, лучи СК и ОА соноправленны. Тогда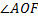 
= 
.
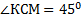Значит, угол между прямыми ОА и CD равен .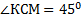
|
|
№46
|
В С
| O |
| 𝛼 |
А D
Дано: АВСD -ромб, m||ВD,m не лежит в плоскости ромба,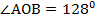 
.
а) Доказать: m и AC -скрещивающиеся
Найти: угол между m и AC.
б) Доказать: m и AD -скрещивающиеся
Найти: угол между m и AD.
Решение. Обозначим плоскость в которой лежит ромб через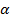 
.
Так как m||ВD, то через них можно провести плоскость . АС пересекает BD в точке О, т.е. пересекает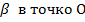 
, О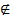 
m,m лежит в .Тогда по признаку скрещивающихся прямых АС и m - скрещивающиеся прямые.
Так как m||ВО, ВО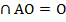 
, то угол между m и AC равен углу между ВО и АО, т.е. 
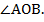По свойству диагоналей ромба 
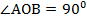, а значит и угол между m и AC равен 
.
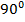б) АD пересекает BD в точке D, т.е. пересекает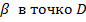 
, D m,m лежит в .Тогда по признаку скрещивающихся прямых АD и m - скрещивающиеся прямые.
Так как m||ВD, ВD 
, то угол между m и AD равен углу между ВD и АD, т.е.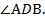 
По свойству диагоналей ромба 
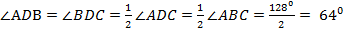, а значит и угол между m и AD равен 
.
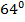Ознакомиться с видеоуроками по ссылкам
Https://infourok.ru/videouroki/1415 (параллельность плоскостей)
Переписать с видеоурока решение задачи 1 и задачи 2.В параграфе это №53,№54 соответственно. Выучить и переписать с учебника в тетрадь решённые задачи- теоремы №55,№58,№59 стр.22-23.
https://infourok.ru/videouroki/1417 (тетраэдр)