Системы трёх линейных уравнений с тремя неизвестными имеют вид:
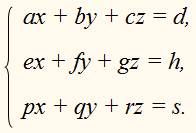
Где a, b, c, d, e, f, g, h, p, q, r, s – заданные числа;
x, y, z –неизвестные.
Числа a, b, c, e, f, g, p, q, r – коэффициенты принеизвестных; d, h, s – свободные члены.
Нормальный вид уравнения первой степени с тремя неизвестными.
Если в уравнении 1 -й степени с 3 неизвестными х, у и z, сделать определённые преобразования, то мы приведем уравнение к такому виду (называемому нормальным), при котором в левой части уравнения находятся только три члена: один с х, другой с у и третий с z, а в правой части будет один член, не содержащий неизвестных.
ПРИМЕР:
Уравнение:
5 х – 3 у – 4 z = –12.
Общий вид его есть следующий:
ах + by + cz = d,
где а, b, с и d какие-нибудь относительные числа.
Неопределенность двух и одного уравнения с тремя неизвестными.
ПРИМЕР:
Предположим, нам дана система 2 уравнений с 3 неизвестными:
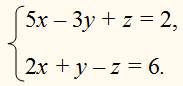
Назначим одному неизвестному, например z, какое-нибудь произвольное число, предположим 1, и подставим это число на место z:
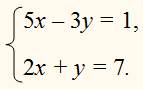
Мы получили таким образом систему 2 уравнений с 2 неизвестными. Решив ее каким-нибудь способом, найдем:
х = 2, у = 3;
значит, данная система с 3 неизвестными удовлетворяется при
х = 2; у = 3; z = 1.
Дадим теперь неизвестному z какое-нибудь иное значение, например z = 0, и подставим это значение в данную систему уравнений, получим:
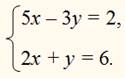
Мы снова получим систему 2 уравнений с 2 неизвестными. Решив ее каким-нибудь способом, найдем:
х = 20 / 11 = 19 / 11;
у = 24 / 11.
Значит, данная система удовлетворяется при
х = 19 / 11;
у = 24 / 11 и
z = 0.
Назначив для z еще какое-нибудь (третье) значение, мы снова получим систему 2 уравнений с 2 неизвестными, из которой найдем новые значения для х и у. Так как для z мы можем назначать сколько угодно различных чисел, то и для х и у можем получить сколько угодно значений (соответствующих взятым значениям z). Значит, 2 уравнения с 3 неизвестными допускают бесчисленное множество решений; другими словами, такая система неопределенна.
Еще большая неопределенность будет, если имеется всего 1 уравнение c 3 неизвестными. Тогда можно будет для каких-нибудь 2 неизвестных назначить произвольные числа; третье же неизвестное найдется из данного уравнения, если подставить в него значения, взятые произвольно для двух неизвестных.
Для того, чтобы можно было найти определенные численные значения для трех неизвестных х, у и z, необходимо, чтобы была задана система 3 уравнений. Такая система может быть решена способом подстановки, а также и способом сложения или вычитания уравнений. Покажем применение этих способов на следующем примере (каждое уравнение предварительно приведено к нормальному виду):
ПРИМЕР:
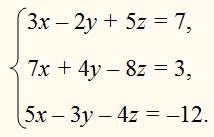
Способ подстановки.
Из какого-нибудь уравнения, например из первого, определим одно неизвестное, например х, как функцию от двух остальных неизвестных:
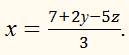
Так как во всех уравнениях х означает одно и то же число, то мы можем подставить найденное выражение на место х в остальные уравнения:
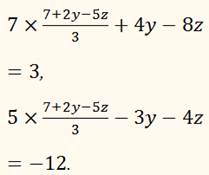
Мы приходим таким образом к системе 2 уравнений с 2 неизвестными у и z. Решив эту систему по какому-нибудь из способов, указанных раньше, найдем численные значения для у и z. В нашем примере это будут значения: у = 3, z = 2; подставив эти числа в выражение, выведенное нами для х, найдем и это неизвестное:
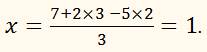
Таким образом, предложенная система имеет решение
х = 1, у = 3, z = 2
(в чем можно убедиться поверкою).
Способ сложения или вычитания.
Из 3 данных уравнений возьмем какие-нибудь два, напр. 1-е и 2-е, и, уравняв в них коэффициенты перед одним неизвестным, напр., перед z, исключим из них это неизвестное способом сложения или вычитания; от этого получим одно уравнение c 2 неизвестными х и у. Потом, возьмем какие-нибудь два других уравнения из 3 данных, напр. 1-е и 3-е (или 2-е и 3-е), и тем же способом исключим из них то же неизвестное т. е. z; от этого получим еще одно уравнение с х и у:
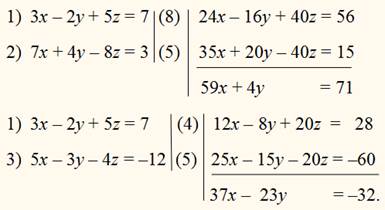
Решим получившиеся два уравнения:
x = 1, у = 3.
Вставим эти числа в одно из трех данных уравнений, например, в первое:
3 × 1 – 2 × 3 + 5 z = 7;
5 z = 7 – 3 + 6 = 10;
z = 2.
Замечание.
Теми же двумя способами мы можем привести систему 4 уравнений с 4 неизвестными к системе 3 уравнений с 3 неизвестными (а эту систему – к системе 2 уравнений с 2 неизвестными и т. д.). Вообще систему m уравнений с m неизвестными мы можем привести к системе m – 1 уравнений с m – 1 неизвестными (а эту систему к системе m – 2 уравнений с m – 2 неизвестными и т. д.).
Некоторые особые случаи систем уравнений.
Случай, когда не все неизвестные входят в каждое из данных уравнений.
ПРИМЕР:
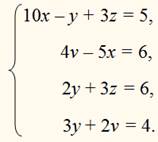
В этом случае система решается быстрее, чем обыкновенно, так как в некоторых уравнениях уже исключены те или другие неизвестные. Надо только сообразить, какие неизвестные и из каких уравнений следует исключить, чтобы возможно скорее дойти до одного уравнения с одним неизвестным. В нашем примере, исключив z из 1-го и 3-го уравнений и v из 2-го и 1-го, получим 2 уравнения с х иу:
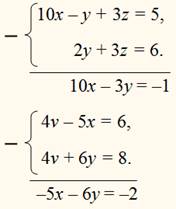
Решив эти уравнения, найдем:
х = 0, y = 1/3 .
Теперь вставим эти числа во 2-е и 3-е уравнения, тогда получим:
v = 3/2 , z = 16/9 = 17/9.
Случай, когда полезно все данные уравнения сложить.
ПРИМЕР:
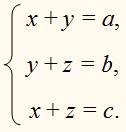
Сложив все три уравнения, найдем:
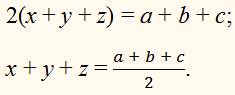
Вычтя из последнего уравнения каждое из данных, получим:
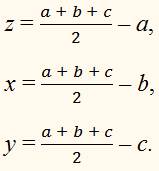
ПРИМЕР:
Решить систему уравнений:
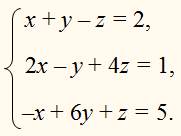
РЕШЕНИЕ:
При решении систем линейных уравнений удобно пользоваться методом Гаусса, который состоит в преобразовании системы к треугольному виду.
Умножаем первое уравнение системы на –2 и, складывая полученный результат со вторым уравнением, получаем
– 3 у +6 z = –3.
Это уравнение можно переписать в виде
у –2 z = 1.
Складывая первое уравнение с третьим, получаем 7у = 7, или у = 1.
Таким образом, система приобрела треугольный вид:
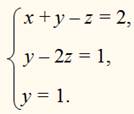
Подставляя у = 1 во второе уравнение, находим z = 0. Подставляя у = 1 и z = 0 в первое уравнение, находим х = 1.
ОТВЕТ: (1; 1; 0)