Признак перпендикулярности плоскостей.

Тема «Перпендикулярность в пространстве»

I. Перпендикулярность прямых в пространстве.

Определение: Две прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом.

Теорема 1. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.

II. Перпендикулярность прямой и плоскости в пространстве.

Определение: Прямая, пересекающая плоскость называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой этой плоскости, проходящей через точку пересечения.

Признак перпендикулярности прямой и плоскости.

Теорема 2 Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.

Свойства перпендикулярных прямой и плоскости.

1свойство: Если плоскость перпендикулярна одной из двух параллельных прямых, она перпендикулярна и другой.

2 свойство: Две прямые, перпендикулярные одной и той же плоскости, параллельны.

Перпендикуляр и наклонная.

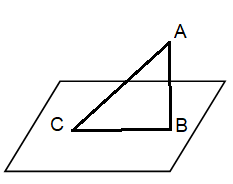Даны плоскость 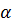и не лежащая на ней точка А.

АВ – перпендикуляр, В – основание перпендикуляра;

АС – наклонная, С – основание наклонной;

СВ – проекция наклонной;

АВ - расстоянием от точки А до плоскости .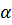

Определение: Перпендикуляром, опущенным из данной точки на плоскость, называется отрезок, соединяющий эту точку с точкой плоскости и лежащий на прямой, перпендикулярной данной плоскости.

Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.

Определение: Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий точку с точкой плоскости, не являющийся перпендикуляром к плоскости.

Конец отрезка, лежащий в плоскости, называется основанием наклонной.

Теорема о трёх перпендикулярах.

Теорема 3 Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна наклонной.

III. Перпендикулярность плоскостей в пространстве.

Определение: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Признак перпендикулярности плоскостей.

Теорема 4 Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Задание. Ответьте письменно на следующие вопросы