пары сил.
Момент силы относительно данной точки –
эффективность вращательного воздействия силы.
*Момент силы F относительно точки О называется
приложенный в центре О вектор mO (F). Модуль
которого = произведению модуля силы на плечо и
который направлен перпенд. плоскости, проходящей
черезцентр О и силу в ту сторону, откуда сила видна
стремящейся повернуть тело вокруг центра О против
часовой.
Момент обозначается:
MO = (F) или mO (F).
Момент силы относительно оси Z равен
Алгебраическому моменту проекции этой силы на
плоскость, перпенд-ую оси Z, взятому относительно
точки пересечения оси с этой плоскостью.
1)Если сила // оси момент=0
2)Усли сила пересекает ось М=0
3)Если сила перпендик. оси, то её
Момент максимален.
Момент пары сил
Парой сил наз-ся система 2ух равных по модулю и
Противоположно напрвленных, параллельных сил.
Пара сил не имеет равнодействующей.
?В отличии от момента силы, момент пары может быть
Приложен в любой точке.
4а Параллельный перенос сил
Теор: Силу, приложенную к телу можно не изменяя
Оказываемого ею действия, переносить из данной
Точки в любую другую точку тела, прибавляя к нему
Пару сил с моментом, равным моменту переносимой
Силы относительно точки переноса
5а Расчет фермы
Ферма-конструкция, состоящая из стержней, соединенных
Между собой по концам шарнирами и образующих
Геометрически неизменяемую систему(мосты подъемники
Краны, и т.д.)
Узел - шарнирное соединение стержней фермы.
Основные допущения при расчетах ферм:
1)Все стержни прямолинейные и передавать могут только
Сжимающиеся или растягивающиеся нагрузки.
2)Трение в шарнирах отсутствует.
|
|
3)Все нагрузки лежат в плоскости фермы и приложены в ее
Узлах.
4)Собственным весом стержней фермы пренебрегаем.
Зависимость между числом стержней m и числом узлов
n фермы без лишних стержней m=2n-3
6а Равновесие пространственной
системы сил:
Условия равновесия: R=0 Mo=0
∑ Fx=0, аналогично у и z
∑mx(F)=0 аналогично у и z
Частные случаи:
1)Система сходящихся сил. Все силы сходятся в одной точке
∑Fz=0 аналогично x и y
2)Система параллельных сил. Действуют параллельные силы
Не лежащие в одной плоскости.
∑Fx=0
∑mx(F)=0 аналогично z
1б Скорости и ускорения точек вращающегося
Тела:
Скорость точки - вектор характеризующий в каждый
Момент времени быстроту и направление ее движения.
При равномерном движении скорость: Uср= S/t
При произвольном движении точки: U= 
=du/dt
В проекции скорости на оси:Ux=dx/dt;
Аналогично для y и z.
Откуда U=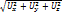 
Ускорением точки – векторная величина, характеризующая
Быстроту изменения скорости с течением времени
a= 
Вращательное движение тела вокруг оси определяется
Углом Φ=f(t) угловая скорость тела ω=𝜟Φ/𝜟t.
2б Скорости точек тела при плоскопараллельном
Движении. МЦС:
Плоскопараллельное движение тела – это когда
Плоская фигура движется в своей плоскости.
-переносное движение – движение некоторого
Центра О тела относительно неподвижн с-мы
координат Хо=f1(t) и Уо=f2(t)
-Относител. Движение- вращение тела вокруг этого
Центра О, определяемого углом Φ=f3(t). Угловая
Скорость фигуры не зависит от выбора центра.
Плоскопараллельное движение изучается двумя
методами: методом разложения сложного движения
|
|
на поступательное и вращательное и методом исклюF
чения скоростей.
Мгновенным центром скоростей (МЦС) является точF
ка на плоскости, абсолютная скорость которой в данF
ный момент равна нулю.
Вокруг этой точки тело совершает поворот со скоростью
ϖ.
Скорость точки А в данный момент равна:
vA = ω0 A,
где n — линейная скорость точки А, вращающейся воF
круг МЦС.
3б Ускорения точек плоской фигуры. МЦУ.
Ускорение точки фигуры = геометрической
Сумме ускорений в поступательном переносном
И вращательном относительном движениях.
aA=a0+ar=a0+am+arτ где arn=r*ω2 а arτ=r*ε
ω и ε – угловые скорость и ускорение тело во
вращательном относительном движении.
Угол Φ можно определить отношением
tgΦ= arτ/ arn= ε/ ω2
Мгновенный центр ускорений(МЦУ):
Пусть а0 известно. Ускорение искомой
Точки С будет складываться из равных
По модулю и противоположных векторов
Переноса а0 и относительно асо ускорений.
Центр лежит на линии ОС, под углом Φ к
Вектору а0. Относительное вращательное
Ускорение асо=ос* 
, следовательно
ос=а0/
4б Вращение тела вокруг неподвижной точки:
Наглядным примером такого движения является
Волчок. Самыми распространёнными являются углы
Эйлера: ψ (пси) – угол процессии, Θ (тета) – угол
между осями, Φ (фи) – угол между линиями узлов.
Положение тела определяется следующим образом.
Назначаются две системы декартовых осей. Первая
система – неподвижные оси x,y,z. Начало которых
берётся в неподвижной точке О тела. Вторая система,
x1,y1,z1. оси, связывается с телом. Поэтому положение
|
|
тела будет определяться как положение этих осей
относительно неподвижных
. 
Когда углы Эйлера равны нулю, подвижные оси совпадают
с неподвижными.
5б Теорема Кориолиса.
Теорема о сложении ускорений(теор.Кориолиса)
При непоступательном переносном движении
абсолютное ускорение точки 
находится как
сумма трех ускорений: относительного 
,
переносного 
и ускорения Кориолиса 
Где, 
-угловая скорость переносного вращения.
1В Аксиомы динамики
1)Закон инерции F=0=>U=const: если на мат-ую точку
Не действуют никакие силы, то эта точка находиться
в покое, или движение прямолинейно и равномерно.
2)Закон зависимости между силой и количеством
Движения(осн. Закон динамики) модуль силы,
Действующей на материальную точку, равен
Произведению массы на ускорение. F=ma
3)Закон равенства действия и противодействия.
F1=F2=>a1*m1=a2*m2 или a1/a2=m2/m1 –
Ускорения.
4) Закон независимости действия сил.
a=a1+a2+…+an, или R=m*a=m(a1+a2+..+an)
2в Д ифференциальные уравнения движения
Точки.
m*d2x/dt2=∑Fix
аналогично с y и z
Если оси естественного трехгранника связать с
Движущейся точкой М: Мτ – касательная к траектории,
Мn –нормаль к траектории в соприкасающ. Плоскости,
Mb-бинормаль.
m*dv/dt=∑Fit, m*v2/p=∑Fin, 0=∑Fib
3в Работа сил.
Эффект действия силы, выражающийся в изменении
энергии материальной точки – работа силы.
A=F*S, A= 
Мощность-скорость соверш. Работы по времени.
Кинетическая энергия – скалярная величина равная
половине произведения массы точки на на квадрат
ее скорости.
Wk=m*U2/2
Силовое поле: Fx=∂U/dx аналогично для Y и Z
Силовое поле – часть пространства в каждой точке
Которого на находящуюся там материальную точку
Действует некоторая сила, зависящая только от
Положения этой точки(X Y Z). Силовая функция такого
Поля U, а поле наз-ся потенциальным.
4в Принцип Даламбера для материальной точки
И системы.
При движении материальной точки в каждый момент
Задания сила реакции и сила инерции уравновешены.
В проекциях на координатные оси, сила инерции будет:
Fинх=-m*d2x/dt2 аналогично для Y и Z.
Проекция на естественные оси составляет:
Fинτ=-m*dv/dt; Fинn=-m*v2/ρ
Метод кинетостатики – метод при решении задач, для
Которых используются ур-ия равновесия статики.
5в Общее уравнение динамики:
По принципу Даламбера материальную систему,
движущуюся под действием некоторых сил,
можно рассматривать находящейся в равновесии,
если ко всем точкам системы приложить их
силы инерции. Значит можно воспользоваться
и принципом возможных перемещений.
В уравнение работ 
добавится еще сумма работ
сил инерции точек на их возможных перемещениях:
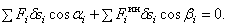
Или по принципу возможных скоростей
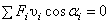
выходит
Эти уравнения называют общим уравнением динамики.
6в Теорема об изменении кинетической
Энергии системы:
Кинетической энергией системы называется скалярная
величина Т, равная арифметической сумме кинетических
энергий всех точек системы.
Если рассмотреть какую-нибудь точку системы с массой mk
имеющую скорость Uk то для этой точки будет
где 
и 
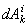- элементарные работы действующих на
точку внешних и внутренних сил. Составляя такие уравнения
для каждой из точек системы и складывая их почленно,
получим
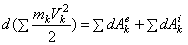
Или
Равенство выражает теорему об изменении кинетической
энергии системы в дифференциальной форме.
1г Метод сечений:
Метод сечений позволяет исследовать внутреннее напряженное
Состояние тела.
Сила упругости – внутренняя сила возникающая внутри тела в
Ответ на внешнее воздействие и непрерывно распределена по
Объему.
1)Мысленно рассекаем брус на 2 части.
2)Одну из частей отбрасываем. Рассматриваем
Оставшуюся часть.
3)Заменяем действие отброшенной части, на оставшуюся,
Системой сил упругости, непрерывно распределен по
Сечению. Приводим их к главному вектору сил и вектору
главного момента.
4)Уравновешиваем силами упругости внешнюю систему сил,
Составляя уравнение равновесия статики: ∑Fx(y)(z)=0;
X(y)(z)=0
2г Напряжение в поперечных сечениях деформированного
Тела:
Интенсивность распределения сил упругости по площади
Поперечного сечения тела определяется вектором полного
Напряжения p=dτ/dA;(Н/м2Па)
Полное напряжение P раскладывается на нормальное
Gi и касательное τi напряжения.
Gi=p*cosα; τi=p*sinα
Напряженное состояние тела будет определено, если
Будут найдены все шесть компонентов напряженного
Состояния: Gx; Gy; Gz; τxy; τyz τzx
Абсолютная деформация – разность между первоначальным
Размером и размером после деформации. 𝜟l=l1-l0
Относительной деформацией называется в общем случае,
Предел отношения ε= 
При линейной деформации εx=𝜟l/l; εy=𝜟b/b
3г Обобщенный закон Гука:
𝜎=εE – закон Гука
Е- модуль упругости первого рода
ε=𝜟l/l
A=1/E; β=-V/E, где V- Коэффициент Пуассона
V=ξy/ξx
G- модуль сдвига второго рода
С=1/G
ξx=AGX+B(Gy+Gz) Yxy=Cτxy
ξy=AGy+B(Gz+Gx) Yyz=Cτyz
ξz=AGz+B(Gx+Gy) Yxz=Cτxy
4г Температурные и технологические деформации:
Тепловое расширение:
𝜟t0=α L 𝜟t0
α-коэффициент линейного расширения
𝜟t0-перепад температур
𝜟 L= 𝜟t0 –𝜟
𝜟-истинное удлинение эл-та в результате
нагрева.
Технологическая деформация
𝜟I=H- 𝜟
H-погрешность изготовления размера.
𝜟-деформация смежных элементов в проекции на ось
Исследуемого элемента.
5г Особые точки диаграммы растяжения:
6г Расчеты на прочность и жесткость при осевом
Растяжении сжатии:
условие прочности, составленное для опасного
сечения, можно записать в таком виде.
Где 𝜎max- максимальное напряжение в конструкции;
[𝜎]- характеристика материала, называемая
допускаемым напряжением.
Допускаемое напряжение находится по формуле
Где 𝜎пред- предельное напряжение, при достижении
которого в стержне наступает предельное состояние
материала: появляются пластические деформации,
если материал стержня – пластичный, или
происходит разрушение, если стержень выполнен
из хрупкого материала; n – нормируемый
коэффициент запаса прочности.
7г Деформация среза (чистый сдвиг):
Чистый сдвиг- напряженное состояние при котором на
Гранях эл-та действуют только касательные напряжения.
Q-перерезывающая сила. А- (поперечная) площадь среза.
Закон Гука F=kx
Кручение-деформация стержня, при которой он нагружается
Парами сил, плоскости действия которых перпендикулярны
его оси.
8г Геометрические характеристики плоских сечений:
Геометрические характеристики – числовые величины
(параметры), определяющие размеры, форму,
расположение поперечного сечения однородного
по упругим свойствам деформируемого элемента
конструкции.
Площадь плоских сечений
Площадь сечения является одной из геометрических
характеристик, используемых, главным образом,
в расчетах на растяжение и сжатие. При расчетах
на кручение, изгиб, а также на устойчивость
используются более сложные геометрические
характеристики: статические моменты, моменты
инерции, моменты сопротивления и т.д
Для вычисления геометрических характеристик
сложных сечений, состоящих из простейших фигур,
они разбиваются на конечное число n простейших
частей. В этом случае
Статическим моментом плоского сечения относительно
некоторой оси называется, взятая по всей его площади А,
сумма произведений площадей элементарных площадок
dA на их расстояния от этой оси.
Статический момент сложного сечения относительно
некоторой оси равен сумме статических моментов всех
частей этого сечения относительно той же оси:
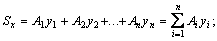
9г Напряжение и деформация в круглом стержне при
Кручении:
Кручением называется такой вид деформации, при
котором в поперечном сечении стержня возникает лишь
один силовой фактор — крутящий момент Мz.
Крутящий момент по определению равен сумме
моментов внутренних сил относительно продольной
оси стержня Oz. Нормальные силы, параллельные оси
Oz, вклада в крутящий момент не вносят. С силами,
лежащими в плоскости поперечного сечения стержня
Мz связывает вытекающее из его определения
уравнение равновесия статики
. 
10г Напряжение в поперечных сечениях при изгибе:
Нормальные напряжения, возникающие при
поперечном изгибе, с достаточной для практических
целей точностью могут определяться по формулам
чистого изгиба. Поэтому условия прочности по
нормальным напряжениям имеют тот же вид, что и
для чистого изгиба.
Касательные напряжения в поперечных сечениях
балки появляются при нагружении балки
сосредоточенными и распределенными силами.
Величина их определяется формулой Журавского:
Где Qy- поперечная сила,
Sотнx- статический момент отсеченной (площади)
части сечения относительно нейтральной
оси. b-ширина сечения, Jx-осевой момент инерции.
11г Дифференциальные уравнения упругой линии
Балки:
Деформированная (изогнутая) продольная ось
балки называется упругой линией, а поступательные
перемещения сечений, равные перемещениям y=y(x)
их центров тяжести сечений – прогибами балки.
Это равенство называется дифференциальным
уравнением упругой линии. При малых деформациях
второе слагаемое в знаменателе мало по сравнению
с единицей (при θ=0.1 рад (y/)2=0.01) и им можно
пренебречь. В результате получим приближенное
дифференциальное уравнение упругой линии балки
12г Продольный изгиб. Формула Эйлера:
ПРОДОЛЬНЫЙ ИЗГИБ- деформация изгиба
прямого стержня при действии продольных
(направленных по оси) сжимающих сил
. 
Формула Эйлера.
1д Этапы проектирования механических устройств:
Основные этапы процесса проектирования.
1. Осознание общественной потребности в
разрабатываемом изделии.
2. Техническое задание на проектирование (первичное описание).
3. Анализ существующих технических решений.
4. Разработка функциональной схемы.
5. Разработка структурной схемы.
6. Метрический синтез механизма (синтез кинематической схемы).
7. Статический силовой расчет.
8. Эскизный проект.
9. Кинетостатический силовой расчет.
10. Силовой расчет с учетом трения.
11. Расчет и конструирование деталей и кинематических пар
(прочностные расчеты, уравновешивание, балансировка, виброзащита).
Здесь целесообразно выполнить следующие действия:
- уточнить служебное назначение сборочной единицы,
- разобрать кинематическую схему узла (механизма), т. е. выделить
составляющие звенья кинематической цепи, уточнить
последовательность передачи энергии от начального звена
по кинематической цепи к конечному звену, выделить
неподвижное звено (корпус, стойку и т.п.), относительно
которого перемещаются все остальные звенья, уточнить
связи между звеньями, т. е. вид кинематических пар,
установить служебные функции неподвижного звена
и всех подвижных звеньев,
- рассчитать восприятие звеньями усилия, так как они
определяют тип и размеры составляющих их деталей,
- начать конструирование узла с наиболее ответственного
звена определить его тип, выделить составляющие
его элементы, расчетом или конструктивно определить
основные размеры элементов кинематических пар и
элементов звена,
- последовательно конструировать все звенья узла,
выполняя проработку их элементов,
- эскизно сконструировать неподвижное звено узла,
- уточнить разделение каждого звена на детали,
- разделить каждую деталь на составляющие элементы,
- установить служебную функцию (функции) и
назначение каждого элемента и его связи с
другими элементами,
- выделить сопрягаемые, прилегающие и свободные
поверхности каждого элемента детали,
- установить окончательно форму каждой поверхности и ее положение,
- окончательно оформить изображение каждой детали
на изображении сборочной единицы.
12. Технический проект.
13. Рабочий проект (разработка рабочих чертежей деталей,
технологии изготовления и сборки).
14. Изготовление опытных образцов.
15. Испытания опытных образцов.
16. Технологическая подготовка серийного производства.
17. Серийное производство изделия.
2д Классификация механических передач:
Конические зубчатые передачи в отличие
от цилиндрических имеют пересекающиеся
оси входных и выходных валов.
Применяются если необходимо изменить
направление кинетической передачи.
червячные - представляют собой механическую
передачу от винта, называемого червяком
на зубчатое колесо, называемое червячным колесом.
Отличаются высоким передаточным отношением,
относительно низким КПД. Червяки бывают однозаходные
и многозаходные. Передаточное отношение червячного
редуктора определяется как отношение количества зубьев
на червячном колесе к количеству заходов на червяке.
гипоидные (спироидные);
цепные;
зубчатыми ремнями;
винтовые.
Передачи трения:
фрикционные;
ремённые.
3д Основной закон зубчатого зацепления:
нормально, проведенная из точки касания
зубьев, делит меж осевое расстояние на
два отрезка, каждый из который обратно
пропорционален скорости угловой скорости
зубьев.
4д Расчет зубчатых передач на прочность по контактным напряжения:
5д Расчет зубьев на выносливость при изгибе
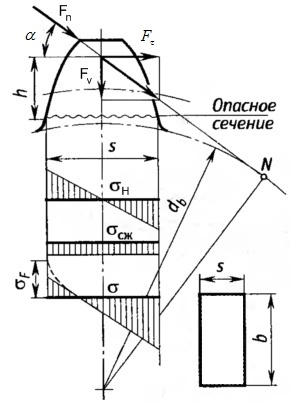
Разрушение зубьев происходит в растянутой зоне,
то есть там, где 
имеет положительный знак.
Для реальных передач учитывается концентрации
нагрузки в контакте зуба от изменения формы тела,
концентрация загруженности в зацеплении,
а также динамические нагрузки в зацеплении.
где, 
– теоретический коэффициент напряженности
в ножке от изменения геометрии формы тела.
С учетом этого получим:
Формула для прямозубых цилиндрических передач
Формула для косозубых цилиндрических передач
где, 
- коэффициент учитывающий
угол наклона зуба,
- коэффициент, торцового перекрытия
- коэффициент, учитывающий одновременное
зацепление нескольких пар зубьев
Формула для конических передач
где, 
- коэффициент учитывающий снижение
несущей способности колеса
- модуль среднего диаметра.
Формула для передачи Новикова
Для уменьшения напряжений следует применять
нарезание зубьев с отрицательным смещением инструмента
или увеличивать модуль зуба.
6д Геометрия зубчатых передач:
7д Червячные зубовинтовые передачи
8д Расчет и проектирование валов
9д Подшипники скольжения и качения
Подшипники скольжения – это опоры вращающихся деталей,
работающие при относительном скольжении цапфы по поверхности подшипника.
Достоинства подшипников скольжения:
малые габариты в радиальном направлении;
возможность работы при высоких скоростях вращения и нагрузках,
в воде и в агрессивных средах;
обеспечение высокой точности установки валов;
малая чувствительность к ударным и вибрационным нагрузкам;
незаменимость в случаях, когда по условиям сборки подшипник
должен быть разъемным (на шейках коленчатых валов).
Недостатки:
выше, чем у подшипников качения, потери мощности на трение;
более сложная смазочная система;
необходимость использования дефицитных материалов.
подшипники качения состоят из наружного и внутреннего колец,
между которыми в сепараторе расположены шарики или ролики.
Сепаратор разделяет тела качения, чтобы они не соприкасались.
Применение подшипников качения позволило заменить трение
скольжения трением качения. Трение качения существенно меньше
зависит от смазки. Условный коэффициент трения качения мал и
близок к коэффициенту жидкостного трения в подшипниках
скольжения (f = 0,0015…0,006). При этом упрощаются система смазки
и обслуживание подшипника.
Преимуществами подшипников качения являются:
небольшие потери на трение;
взаимозаменяемость, облегчающая монтаж и ремонт подшипниковых узлов;
малые пусковые моменты;
нетребовательность к смазке и уходу (за исключением случаев, когда от подшипников,
например, роторов авиационных двигателей, необходимо отводить тепло).
Недостатками подшипников качения являются:
чувствительность к ударам и вибрациям вследствие большой жесткости подшипника;
сравнительно большие радиальные габаритные размеры;
шум при работе с высокой частотой вращения.
10д Классификация соединения деталей:
11д Сварочные и заклепочные соединения:
Заклепочные и сварные соединения
относятся к неразъемным соединениям,
которые можно разобрать только путем
разрушения или повреждения соединенных
деталей или их шва.
Заклепочным соединением называется
соединение двух деталей заклепками.
Заклепочные швы различают:
по назначению — прочные, прочно-плотные и плотные;
по числу рядов — однорядные, двухрядные и многорядные;
по числу сечений — односрезные и двухсрезные;
по типу стыка — внахлестку и встык;
по расположению заклепок — с параллельными
рядами и с расположением в шахматном порядке.
Сварные соединения. Сварные соединения получили
преимущественное применение по сравнению
с заклепочными соединениями. Это определяется тем,
что сварка позволяет изготовить облегченную
конструкцию шва, уменьшает трудоемкость работ,
создает плотность и непроницаемость шва.
12д Прессовые соединения и их расчет:
Прессовые соединения отнесены к группе неразъемных
условно, так как они позволяют производить повторную
сборку и разборку, однако с применением значительных
усилий и частичным повреждением сопрягаемых поверхностей
деталей. Прессовые соединения. Задача упрочнения
прессовых соединений заключается прежде всего
в уменьшении давления на посадочных поверхностях
и напряжений в охватывающей и охватываемой деталях
рациональным выбором параметров соединения
(диаметра и длины посадочной поверхности, толщины
стенок охватывающей и охватываемой детали.
Расчет прессовых соединений на коррозионно-механическо
е изнашивание пока не разработан, но известны метод
снижения или даже устранения этого вида изнашивания:
повышение твердости поверхностей посадки; уменьшение
напряжений путем увеличения диаметра в месте посадки;
увеличение давления посадки, а следовательно, и сил трения,
которое сокращает распространение деформаций внутрь ступицы
и уменьшает относительные перемещения; образование кольцевых
проточек по торцам ступицы. Эти проточки увеличивают
податливость ступицы, позволяют ей деформироваться вместе
с валом и уменьшают микросдвиги. Резьбовым называют соединения составных частей изделия с применением детали, имеющей резьбу.
13д Виды резьбовых соединений и их расчет метрической резьбы:
Резьбовым называют соединения составных
частей изделия с применением детали, имеющей резьбу.
Виды разъемных соединений:
Резьбовые,шпоночные, шлицевые, клиновые,
штифтовые, профильные.