Лекция 1. СВЕТОВЫЕ ВОЛНЫ
Волновой процесс или волна – это процесс распространения колебаний в сплошной среде. Основным свойством всех волн является перенос энергии без переноса вещества.
В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных волнах частицы среды колеблются в плоскостях, перпендикулярных направлению распространения волны.
Длина волны – это расстояние между ближайшими частицами, колеблющимися в одинаковой фазе. Длина волны равна расстоянию, на которое распространяется волна за время, равное периоду колебаний: 
, где v – скорость распространения волны (фазовая скорость 
).
Волновой фронт – это геометрическое место точек, до которых доходят колебания в к определенному моменту времени.
Волновая поверхность – это геометрическое место точек, колеблющихся в одинаковой фазе.
Волна называется плоской, если ее волновые поверхности представляют собой совокупность плоскостей, параллельных друг другу. Уравнение плоской волны 
.
Волна называется сферической, если ее волновые поверхности имеют вид концентрических сфер (центр их называют центром волны). Уравнение сферической волны 
, где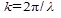 
– волновое число.
Оба эти уравнения являются решением волнового уравнения 
, где 
– оператор Лапласа.
Если в среде распространяется сразу несколько волн, то для них справедлив принцип суперпозиции.
Любая волна может быть представлена в виде волнового пакета, т.е. суперпозиции волн, мало отличающихся друг от друга по частоте, занимающей в каждый момент времени ограниченную область пространства. Скорость движения волнового пакета – групповая скорость – равна 
.
Различают волны бегущие, которые переносят в пространстве энергию (к ним относятся плоская и сферическая волны), и волны стоячие, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами. В стоячей волне переноса энергии не происходит. Уравнение стоячей волны 
.
Амплитуда стоячей волны достигает максимума в точках с координатами 
, называемых пучностями стоячей волны. Амплитуда стоячей волны обращается в ноль в точках 
. Длина стоячей волны 
.
Электромагнитные волны – это переменное электромагнитное поле, распространяющееся в пространстве с конечной скоростью.
Существование электромагнитных волн вытекает из уравнений Максвелла: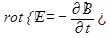 
. Отсюда для области пространства, не содержащей свободных электрических зарядов и макроскопических токов, и среды, представляющей собой однородный и изотропный диэлектрик, не обладающий сегнетоэлектрическими или ферромагнитными свойствами, можно получить волновые уравнения для векторов 
и 
:
, 
, где – оператор Лапласа; 
– фазовая скорость электромагнитной волны, 
– скорость света в вакууме; 
– показатель преломления среды.
Таким образом, электромагнитные поля действительно могут существовать в виде электромагнитных волн
Поскольку 
, то 
– скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме
Следствия теории Максвелла:
1) Векторы и напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору 
скорости распространения волны, причем векторы , и образуют правовинтовую систему.
2) В электромагнитной волне векторы Е и Н всегда колеблются в одинаковых фазах, причем мгновенные значения Е и Н в любой точке связаны соотношением 
.
Волновым уравнениям: 
, 
удовлетворяют плоские монохроматические электромагнитные волны, описываемые уравнениями 
, 
где 
и 
– амплитуды напряженностей электрического и магнитного полей волны, ω – круговая частота волны, 
– волновое число, φ – начальная фаза колебаний (одинаковая, поскольку колебания и происходят с одинаковой фазой).
Объемная плотность энергии электромагнитной волны складывается из объемных плотностей 
и 
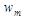электрического и магнитного полей:
Плотность потока энергии 
.
Вектор 
плотности потока энергии электромагнитной волны называется вектором Умова – Пойнтинга. 
Вектор направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
Скалярная величина I, равная модулю среднего значения вектора Умова – Пойнтинга, называется интенсивностью волны: 
.
Интенсивность волны численно равна энергии, переносимой волной за единицу времени сквозь единицу площади поверхности, нормальной к направлению распространения волны. Интенсивность синусоидальной волны пропорциональна квадрату ее амплитуды.
Шкала электромагнитных волн приведена на рис.