Возможность преобразовывать матрицы операторов (формула (6)) посредством перехода к новому базису заставляет представить матрицу оператора в более удобном для преобразования виде с сохранением её ранга. Это диагональный вид матрицы. Пусть оператор  представлен недиагональной матрицей А =
представлен недиагональной матрицей А =  в произвольном базисе е. Можно ли перейти к новому базису, в котором оператор
в произвольном базисе е. Можно ли перейти к новому базису, в котором оператор  будет иметь диагональную матрицу?
будет иметь диагональную матрицу?
Определение1. Ненулевой вектор х называется собственным вектором линейного оператора  , если найдется такое число λ, называемое собственным значением линейного оператора, что
, если найдется такое число λ, называемое собственным значением линейного оператора, что
 = λ ∙х (7)
= λ ∙х (7)
Среди векторов линейного пространства могут существовать такие, воздействие оператора на которые переводит эти векторы в коллинеарные самим себе. Если на таких векторах построить базис, преобразования линейной алгебры значительно упростятся.
Не всякий линейный оператор обладает собственными векторами. Например, в геометрической плоскости R2 оператор поворота на угол, не кратный π, не имеет ни одного собственного вектора, поскольку ни один ненулевой вектор после поворота не останется коллинеарным самому себе.
Решим задачу нахождения собственных векторов оператора. Запишем равенство (7) в матричной форме А·Х = λ·Х. Преобразуем матричное уравнение А·Х - λ·Х = 0, А·Х - λ·Е·Х = 0, (А - λ·Е)· Х = 0,
где Е – единичная матрица порядка n, а вектор Х =  размера n⤫1.
размера n⤫1.
Матричное уравнение (А - λ·Е)· Х = 0 имеет вид при переходе к покоординатному равенству: 
 (8)
(8)
Нас интересуют ненулевые решения однородной системы, поэтому приравняем определитель однородной системы к нул  ю: det (A – λE)=0
ю: det (A – λE)=0
или  = 0 (9)
= 0 (9)
Левая часть уравнения (9) называется характеристическим многочленом матрицы А: 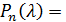 det (A – λE). Это многочлен n – ой степени, он может иметь не более n действительных корней.
det (A – λE). Это многочлен n – ой степени, он может иметь не более n действительных корней.
Корни этого многочлена  являются собственными значениями матрицы А и обладают следующими свойствами:
являются собственными значениями матрицы А и обладают следующими свойствами:
1) 
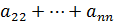 ,
,
2)  .
.
При последовательной подстановке  в систему (8) для каждого λ находится ненулевое решение однородной системы (8) – собственный вектор линейного преобразования, заданного матрицей А.
в систему (8) для каждого λ находится ненулевое решение однородной системы (8) – собственный вектор линейного преобразования, заданного матрицей А.
Алгоритм нахождения собственных векторов матрицы А
1. Составить матрицу А- λЕ и характеристическое уравнение
det (A – λE)=0.
2. Найти корни характеристического уравнения  .
.
3. Подставить значение корня  в однородную систему (8) и найти соответствующий собственный вектор - ненулевое решение однородной системы.
в однородную систему (8) и найти соответствующий собственный вектор - ненулевое решение однородной системы.
Пример. Найти собственные векторы матрицы А =  .
.
Решение. Составим матрицу А- λЕ =  и перейдем в соотношении (А - λ·Е)· Х = 0 к покоординатному равенству
и перейдем в соотношении (А - λ·Е)· Х = 0 к покоординатному равенству
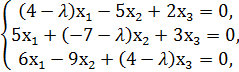 (10)
(10)
где  координаты собственного вектора Х. Составим характеристическое уравнение матрицы А для нахождения собственных значений: det (A – λE) = 0 или
координаты собственного вектора Х. Составим характеристическое уравнение матрицы А для нахождения собственных значений: det (A – λE) = 0 или  .
.
Имеем det (A – λE) = (4-λ) 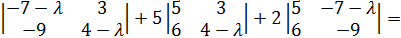
=-  .
.
Характеристическое уравнение -  имеет действительные корни
имеет действительные корни 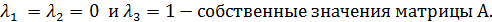
Найдем собственный вектор  , отвечающий собственному значению
, отвечающий собственному значению 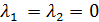 , для чего это значение λ = 0 подставим в однородную систему (10)
, для чего это значение λ = 0 подставим в однородную систему (10)

При  определитель этой системы равен нулю, поэтому однородная система имеет бесконечное множество ненулевых решений. Найдем их методом Гаусса
определитель этой системы равен нулю, поэтому однородная система имеет бесконечное множество ненулевых решений. Найдем их методом Гаусса

4С2 – 5С1→С2/ С3-С2→С3/
2С3 - 3С1 →С3/
Получим равносильную систему трапецеидального вида:


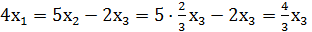 или
или 
Положим х3 = 3t, тогда х2= 2 t, х1= t, получим собственный вектор
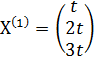 , где t
, где t  .
.
Рассуждая аналогично, получим при 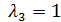
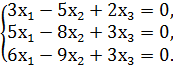
Найдем ненулевые решения этой системы
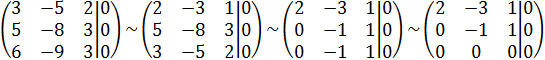
С3:3→С1/ 2С2-5С1→С2/ С3-С2→С3/
С1→С3/ 2С3-3С1→С3/
Имеем однородную систему  откуда следует
откуда следует
 2х1 = 3х2-х3=3х3-х3=2х3 или
2х1 = 3х2-х3=3х3-х3=2х3 или  Положим
Положим  получим собственный вектор
получим собственный вектор  , где s
, где s  .
.
Ответ:  , где t
, где t  ;
;

 ,
,  , где s
, где s  .
.
Замечания.
1) det (A – λE) не зависит от выбора базиса. В самом деле, преобразуем характеристический многочлен det (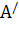 – λE), полученный в новом базисе
– λE), полученный в новом базисе  ), если известна матрица Т перехода от старого базиса е = (е1 , е2 , …, еn) к новому. С учетом А/ = Т-1 ∙ А ∙ Т (см. формулу (6)), получим det (
), если известна матрица Т перехода от старого базиса е = (е1 , е2 , …, еn) к новому. С учетом А/ = Т-1 ∙ А ∙ Т (см. формулу (6)), получим det (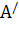 – λE) = det (
– λE) = det ( – λE) = det (
– λE) = det ( – λ
– λ  E∙Т) = det (
E∙Т) = det ( – λ
– λ 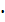 E)∙Т).
E)∙Т).
Учитывая, что определитель произведения квадратных матриц одинакового порядка равен произведению определителей этих матриц, получим: det ( – λE)= det (
– λE)= det ( – λ
– λ 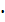 E) ∙ detТ= det (A – λE).
E) ∙ detТ= det (A – λE).
2) Если линейный оператор имеет n попарно различных собственных значений, то соответствующие им собственные векторы линейно независимы, и матрица этого оператора в базисе, состоящем из его собственных векторов, имеет диагональный вид, где по главной диагонали стоят собственные числа. Пусть е1 , е2 , …, еn – собственные векторы линейного оператора, соответствующие его собственным значениям  . Собственные векторы примем за базисные.
. Собственные векторы примем за базисные.
Тогда  и согласно (3):
и согласно (3):

откуда 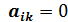 при i
при i 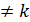 , и
, и 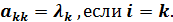
Таким образом, матрица оператора  в базисе, состоящем из его собственных векторов, является диагональной и имеет вид
в базисе, состоящем из его собственных векторов, является диагональной и имеет вид
А/=  .
.
3) Собственные векторы симметричной матрицы, отвечающие различным собственным значениям, ортогональны.
4) Характеристический многочлен симметричной матрицы имеет только действительные корни.
Линейная модель обмена
В качестве примера математической модели экономического процесса, приводящего к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Пусть имеется n стран S1, S2, …, Sn, национальный доход каждой из которых равен соответственно  . Обозначим коэффициентами
. Обозначим коэффициентами  долю национального дохода, которую страна Sj тратит на покупку товаров у страны Si. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
долю национального дохода, которую страна Sj тратит на покупку товаров у страны Si. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
 (11)
(11)
Рассмотрим матрицу А =  , которую называют структурной матрицей международной торговли. Согласно (11) сумма элементов любого столбца этой матрицы равна единице.
, которую называют структурной матрицей международной торговли. Согласно (11) сумма элементов любого столбца этой матрицы равна единице.
Для любой страны Si (i= 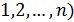 выручка от внутренней и внешней торговли составит: pi =
выручка от внутренней и внешней торговли составит: pi =  .
.
Для сбалансированной торговли необходима бездефицитность торговли каждой страны Si, т.е. выручка от торговли каждой страны должна быть не меньше её национального дохода:  (i=
(i= 
Если считать  (i=
(i= 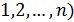 , то подучим систему неравенств
, то подучим систему неравенств
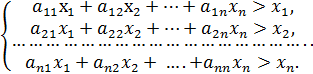 (12)
(12)
Сложив все неравенства системы (12), получим после группировки
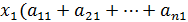 )+
)+  +
+  +…+
+…+  )+…
)+…
 +
+  +
+  +…+
+…+  )
)  .
.
Учитывая (11), выражения в скобках равны единице, и мы приходим к противоречивому неравенству  .
.
Таким образом, неравенство 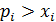 (i=
(i= 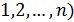 невозможно, и условие
невозможно, и условие  принимает вид
принимает вид  (i=
(i= 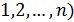 . С экономической точки зрения все страны не могут одновременно получать прибыль.
. С экономической точки зрения все страны не могут одновременно получать прибыль.
Введем вектор х = (  ) национальных доходов стран, получим матричное уравнение АХ=Х, в котором вектор х записан в виде столбца, т.е. задача свелась к отысканию собственного вектора матрицы А, отвечающего собственному значению λ=1.
) национальных доходов стран, получим матричное уравнение АХ=Х, в котором вектор х записан в виде столбца, т.е. задача свелась к отысканию собственного вектора матрицы А, отвечающего собственному значению λ=1.
Пример. Структурная матрица торговли трех стран S1, S2, S3 имеет вид А =  Найти соотношение национальных доходов стран для сбалансированной торговли.
Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение. Найдем собственный вектор х,отвечающий собственному значению λ=1, решив уравнение (А-Е)Х=0 или систему
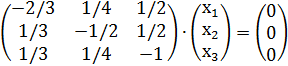
методом Гаусса.
Найдем 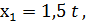

 , т.е. х = (
, т.е. х = (  ).
).
Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов х = (  ) т.е. при соотношении национальных доходов стран 3/2:2:1 или 3:4:2.
) т.е. при соотношении национальных доходов стран 3/2:2:1 или 3:4:2.