Механическая система и ее центр масс. Уравнение изменения
Импульса механической системы.
Максвелловское распределение молекул по скоростям.
3. Найти потенциальную энергию тела массой m = 400 кг на расстоянии r = 7600 км от центра Земли. Величину потенциальной энергии на бесконечно большом расстоянии считать равной нулю. Радиус Земли R = 6400 км..
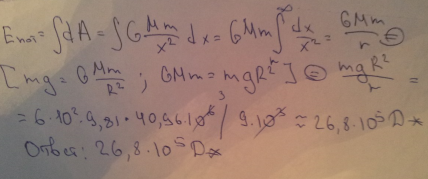
4. Во сколько раз следует увеличить изотермически объем идеального газа в количестве 5 молей, чтобы изменение энтропии стало равно 24 Дж/кг?
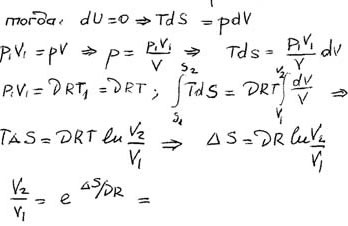
Билет:
1. Распределение энергии по степеням свободы молекул. Внутренняя энергия идеального газа. 
2. Динамика материальной точки. Силы в механике.
3. Вычислить работу А, совершаемую при равноускоренном подъёме груза массой m=300 кг на высоту h=16 м за время t=20 c.
4. Найти изменение энтропии при нагревании воды массой 0,6 кг от температуры 20 рС до температуры 100 оС и последующим превращении воды в пар той же температуры. Удельная теплоемкость воды С=4,2×103 Дж/кг*К. Удельная теплота парообразования λ= 334×103 Дж/кг. 
Билет:
1. Основное уравнение молекулярно-кинетической теории идеального
Газа.
2.Классический закон сложения скорости и ускорения материальной точки в случае поступательного движения систем отсчёта.
3. Шар и цилиндр, имеющие одинаковые массы и радиусы, катятся по горизонтальной плоскости без скольжения с одинаковой скоростью. Найти отношение кинетических энергий этих тел.
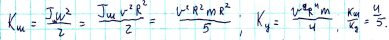
4. Найти КПД цикла, состоящего из двух изобар и двух адиабат, если в пределах цикла давление изменяется в n раз. Рабочее вещество идеальный газ с показателем адиабаты γ. 
|
|
Билет:
1. Явление переноса в газах. Теплопроводность газов.
2. Статистическое обоснование второго начала термодинамики. Формула Больцмана для статистической энтропии.
3. Кинетическая энергия электрона равна 1,2 МэВ. Определить скорость электрона.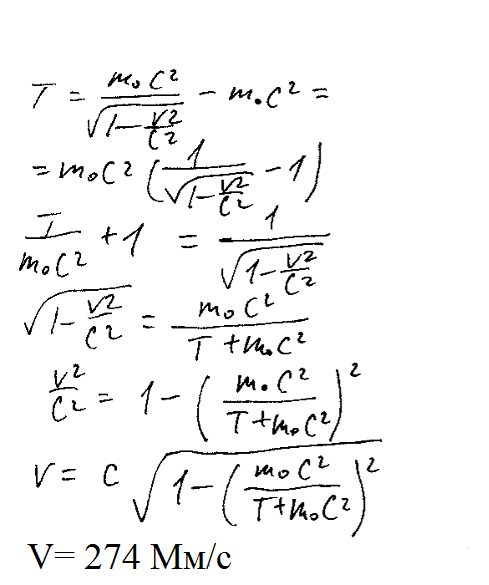 
4. Собственные частоты двух диссипативных колебательных систем отличаются в 1,5 раза, а коэффициенты затухания отличаются в 2 раза. Определить коэффициенты затухания этих систем, если их резонансные частоты равны, а частота одной из них равна 100 Гц.
Билет:
1. Закон сохранения механической энергии. 
2. Релятивистский закон сложения скоростей.
3. Тепловая машина работает по прямому циклу 1-2-3-4-1, которая состоит из изохорны 1-2, двух изобар 2-3 и 4-1, а также изотермы 3-4 с отдачей тепла холодильнику. При этом P2=P3 < P1=P4.Изобразить этот цикл в переменных P-V, P-T, V-T.
3. Холодильная машина работает по обратному циклу Карно в интервале температур от t1 = -100C доt2 = 3000C. Рабочее тело - азот, масса которого m = 0,4 кг. Найти количество теплоты, отбираемого от охлаждаемого тела, и работу внешних сил за цикл, если отношение максимального объёма к минимальному равно 3.
Билет:
1. Интервал между событиями в релятивистской механике. 
2. Внутренняя энергия термодинамической системы. Теплота и работа. Первое начало термодинамики. 
3. На какой высоте над поверхностью Земли атмосферное давление вдвое меньше, чем на ее поверхности? Считать, что температура воздуха равна 300 К и не изменяется с высотой.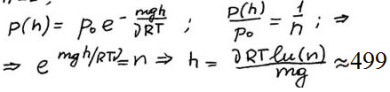
4. Два физических маятника совершают малые колебания вокруг одной оси с частотами υ1 и υ2. Моменты инерции этих маятников относительно данной оси равны соответственно I1 и I2. Маятники жестко соединили друг с другом. Определить период малых колебаний составного маятника.
|
|
Билет:
1. Плоская гармоническая волна, длина волны, фазовая скорость, волновой вектор. Сферическая волна. 
2. Неравенства Клаузиуса. Термодинамическая энтропия. Третье начало термодинамики.
3. Полная энергия релятивистской частицы возросла на 1,4 Дж. На сколько при этом изменится кинетическая энергия частицы?
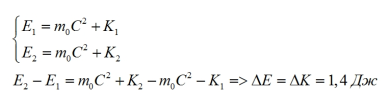
4. Два электрона движутся вдоль одной прямой со скоростями v1 = 0,9С и v2 = 0,8С. Определить скорость электронов относительно друг друга, если электроны движутся навстречу друг другу.
Билет:
1. Упругие волны в стержнях. Волновое уравнение.
В ограниченных твёрдых телах (пластина, стержень), представляющих собой твёрдые волноводы акустические, могут распространяться только нормальные волны,каждая из к-рых является комбинацией неск. продольных и сдвиговых волн, распространяющихся под острыми углами к оси волновода и удовлетворяющих граничным условиям: отсутствию механич. напряжений на поверхности волновода. Число п нормальных волн в пластине или стержне определяется толщиной или диаметром d, частотой w и модулями упругости среды. При увеличении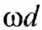 
число нормальных волн возрастает, и при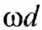 
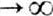, n 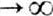. Нормальные волны характеризуются дисперсией фазовой и групповой скоростей.В бесконечной пластине существуют два типа нормальных волн-Лэмба волны и сдвиговые волны. Плоская волна Лэмба характеризуется двумя составляющими смещений, одна из к-рых параллельна направлению распространения волны, другая-перпендикулярна граням пластины. В плоской сдвиговой нормальной волне смещения параллельны граням пластины и одновременно перпендикулярны направлению распространения волны. В цилиндрич. стержнях могут распространяться нормальные волны трёх типов - продольные, изгибные, крутильные. 
2. Цикл Карно. Коэффициент полезного действия идеальной тепловой машины. 
3. На толкание ядра массой m=3 кг, брошенного под углом α=30 к горизонту, затраченная работа равная А=150 Дж. Через какое время ядро упадёт на землю?
|
|
4. Газ массой m и молярной массой M находится под давлением P между двумя одинаковыми горизонтальными пластинами. Температура газа растет линейно от T1 у нижней пластины до T2 у верхней. Найти объём газа между пластинами.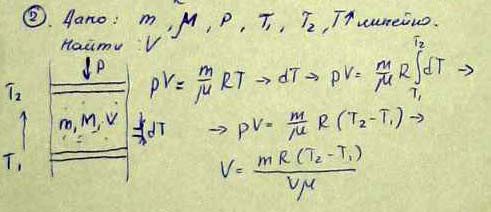 
бИЛЕТ:
1. Вынужденные колебания. Механический резонанс. 
2. Тепловые и холодильные машины. Второе начало термодинамики. Теорема Карно. 
Шарик конический маятник, длина нити которого равна l, движется по окружности со скоростью v. Определить угол отклонения нити от вертикали.
4.Определить скорость звука в воздухе при нормальном условиях, если считать, что процессы сжатия и расширения воздуха в волне происходят адиабатически. Молярная масса воздуха равна µ=29*10^-3 кг/моль. Скорость звука определяется по формуле с=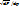 
.
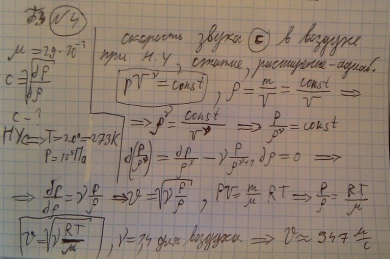
Билет:
1. Сложение взаимно перпендикулярных гармонических колебаний равных и кратных частот. 
2. Теплоемкость идеального газа при изопроцессах. 
3. Снаряд, летящий со скоростью V0 = 200 м/с, разорвался на два осколка. Осколок, у которого масса составляет 0,6 массы снаряда, продолжает двигаться в прежнем направлении, но со скоростью V1 = 300 м/с. Найти скорость другого осколка.
4. Азот массой m = 84 г адиабатически расширили в n = 3 раза, а затем изобарно сжали до начального состояния. Определить изменение энтропии газа при его переходе из начального состояния в конечное состояние.
Билет:
1. Гармонические колебания. Сложение гармонических колебаний одного направления близких частот.
2. Эквивалентность теплоты и работы. Внутренняя энергия термодинамической системы. Первое начало термодинамики. 3. В баллоне v=40 находится кислород. Кинетическая энергия всех молекул кислорода в баллоне равна Е=8. Определить давление, которое создаёт этот газ.
Средняя кинетическая энергия поступательного движения молекул кислорода:
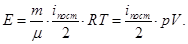
Давление кислорода: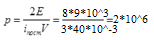 
4. Лодка массой m = 120 кг движется с начальной скоростью V0 = 1 м/с. Считая, что сила сопротивления воды пропорциональна скорости F = -kV, где k = 10 кг/с - коэффициент сопротивления. Определить скорость лодки через 12 с. после начала движения.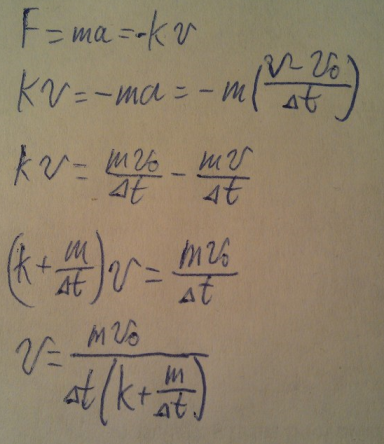
Билет:
1. Гармонические колебания. Векторная диаграмма. Сложение гармонических колебаний одного направления равных частот. 
2. Агрегатные состояния вещества. Условия равновесия фаз. Фазовый переход I и II рода.
При описании пространственно неоднородных сред применимо разбиение их на некоторое число однородных по своему составу частей, разделенных границами раздела. Макроскопическая часть среды (вещества), имеющая однородный физико-химический состав, называется фазой.
Условия равновесия фаз.
Для равновесия фаз необходимо, чтобы между ними наблюдалось тепловое и механическое равновесие. Первое из этих условий означает равенство температур Т1 и Т2 с разных сторон границы раздела фаз: Т1=Т2=Т. Второе условие не обязательно соответствует равенству давлений Р1 и Р2 с разных сторон границы раздела, так как сама эта граница, в случае, если её форма не представляет собой плоскости, может создавать дополнительное межфазное давление 
. Поэтому в общем случае условие механического равновесия имеет вид: P2=P1+ , где: - дополнительное давление на первую фазу, создаваемое границей её раздела со второй. Если считать границы раздела фаз плоскими, то условие P2=P1+ станет эквивалентным предположению о равенстве давлений по обе стороны границы раздела фаз: P1=P2=P.
3. Диск радиусом R=60 см вращается вокруг вертикальной оси. На краю диска лежит кубик. Найти частоту n вращения диска, при которой кубик соскользнёт с диска. Коэффициент трения µ=0,2. 
4.При адиабатическом расширении кислорода с начальной температурой Т1=300К внутренняя энергия уменьшилась на U=-10 кДж, а его объём увеличился в 12 раз. Определить массу m кислорода.
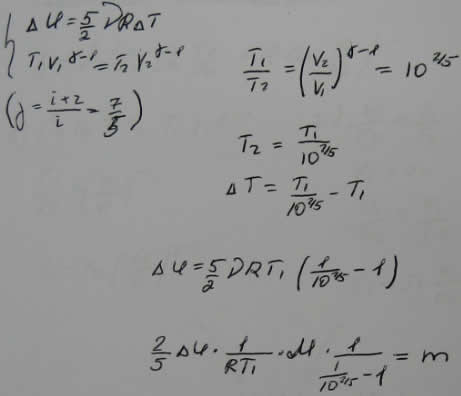
Ответ: 14,5
Билет:
1. Явление на границе газа, жидкости и твердого тела. Капиллярные явления.
2. Эффект Джоуля-Томпсона. Принцип Ле-Шателье-Брауна.
Эффект Джоуля-Томпсона:
(Дроссельэффект) заключается в изменении температуры газа при его адиабатическом (без теплообмена с окружающей средой) дросселировании, т.е. протекании через пористую перегородку, диафрагму или вентель. Эффект называется положительным, если температура газа при адиабатическом дросселировании понижается, и отрицательным, если она повышается. Для каждого реального газа существует точка инверсии - значение температуры при которой измеряется знак эффекта. Для воздуха и многих других газоз точка инверсии лежит выше комнатной температуры и они охлаждаются в процессе Джоуля-Томсона. Дросселирование - один из основных процессов, применяемых в технике снижения газов и получения
сверхнизких температур. Способ определения термодинамических величин газов, например, энтальпии, путем термостатировакия исходного газа, дросселирования его с последующим измерением тепла, подзеденного Джо к газу, отличающийся тем. что с целью определения термодинамических величин газов с отрицательным эффектом Джоуля-Томсона. Газ после
дросселирования охлаждают до первоначальной температуры, затем нагревают до температуры после дросселя с измерением подведенного к нему тепла и по известным соотношениям определяют искомые величины.
Принцип Ле-Шателье-Брауна:
Внешнее воздействие, выводящее систему из термодинамического равновесия, вызывает в ней процессы, стремящиеся ослабить результаты этого воздействия.
-Увеличение давления смешает равновесие в сторону реакции, зедушей к уменьшению объема.
-Повышение температуры смешает равновесие в сторону эндотермической реакции.
-Увеличение концентрации исходных вешеств и удаление продуктов из сферы реакции смешают равновесие в строну прямой реакции.
- Катализаторы не влияют на положение равновесия.
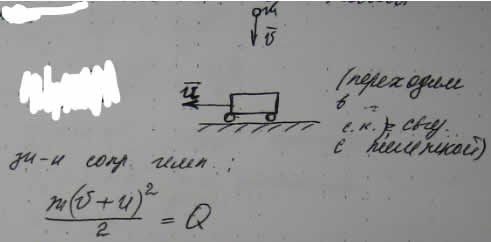
3. Пуля массой 8 г внедряется с начальной скоростью 200 м/с в очень массивную мишень с песком, которая движется на встречу пуле со скоростью 100 м/с. Какое количество теплоты выделится при полном торможении пули.
4. О пределить массу атмосферы земли при условии, что температура атмосферы не изменяется по высоте, т.е. Т=const, а давление на поверхности земли 1 атм. 
Билет:
1. Связь между потенциальной энергией и силой. Потенциальная энергия тяготения и упругих деформаций.
Пространство, в котором действуют консервативные силы, называется потенциальным полем. Каждой точке потенциального поля соответствует некоторое значение силы F, действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой F и U должна быть связь, с другой стороны, dA = –dU, следовательно Fdr=-dU, отсюда: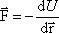 
Проекции вектора силы на оси координат: 
Вектор силы можно записать через проекции: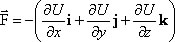 
, F = –grad U, где 
.
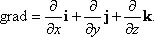Градиент – это вектор, показывающий направление наибыстрейшего изменения функции. Следовательно, вектор направлен в сторону наибыстрейшего уменьшения U. Потенциальная энергия упругой деформации (пружины) Найдём работу, совершаемую при деформации упругой пружины.
Сила упругости Fупр = –kx, где k – коэффициент упругости. Сила непостоянна, поэтому элементарная работа dA = Fdx = –kxdx.
(Знак минус говорит о том, что работа совершена над пружиной). Тогда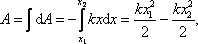 
, т.е. A = U1 – U2. Примем: U2 = 0, U = U1, тогда 
.
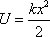На рис. 5.5 показана диаграмма потенциальной энергии пружины.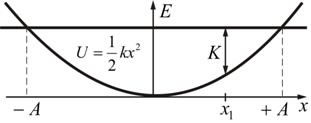 
Рис. 5.5
Здесь E = K + U – полная механическая энергия системы, К – кинетическая энергия в точке x1.