2.1. Геометрическое изображение комплексных чисел. Пусть a = a + bi ¾ произвольное комплексное число. Тогда в декартовой системе координат существует единственная точка с координатами (a; b) и, обратно, произвольной точке (a; b) в декартовой системе координат соответствует единственное комплексное число a такое, что Re a = a и Im a = b. Таким образом, между точками плоскости и множеством комплексных чисел C существует взаимно однозначное соответствие y такое, что y (a + bi)=(a; b). Поэтому комплексные числа можно изображать точками плоскости. Эту плоскость называют комплексной.
 Пусть M (a; b) ¾ точка комплексной плоскости, соответствующая комплексному числу a + bi. Тогда можно рассматривать вектор
Пусть M (a; b) ¾ точка комплексной плоскости, соответствующая комплексному числу a + bi. Тогда можно рассматривать вектор  с координатами (a; b) (рис. 1) Вектор
с координатами (a; b) (рис. 1) Вектор  называется векторным представлением числаa + bi. Длина |
называется векторным представлением числаa + bi. Длина |  | вектора
| вектора  называется модулем комплексного числа a = a + bi, а угол j между вектором
называется модулем комплексного числа a = a + bi, а угол j между вектором  и положительным направлением оси Ox называется аргументом комплексного числа a ¹0. Для нуля модуль не определён. Модуль числа a обозначается через | a |, а его аргумент ¾ через Аrg a. Очевидно, Аrg a определён с точностью до кратных угла 2 p, то есть, если j ¾ угол наклона
и положительным направлением оси Ox называется аргументом комплексного числа a ¹0. Для нуля модуль не определён. Модуль числа a обозначается через | a |, а его аргумент ¾ через Аrg a. Очевидно, Аrg a определён с точностью до кратных угла 2 p, то есть, если j ¾ угол наклона  к оси Ox, то Аrg a = j +2 p k, k Î Z. Если j =Аrg a Î(p, p ], то j называется главным значением аргумента и обозначается через arg a. Таким образом, Аrg a =arg a +2 p k, k Î Z, arg a Î(- p, p ].
к оси Ox, то Аrg a = j +2 p k, k Î Z. Если j =Аrg a Î(p, p ], то j называется главным значением аргумента и обозначается через arg a. Таким образом, Аrg a =arg a +2 p k, k Î Z, arg a Î(- p, p ].
2.1.1. Упражнение. Построить точки, изображающие комплексные числа 1, -1, i, - i, 1+ i, 1- i, 2+3 i, 2-3 i.
2.1.2. Упражнение. Изобразить на плоскости множество точек, соответствующих комплексным числам z, удовлетворяющим условиям:
а) | z |=2; б) | z -(2+3 i)|=1; в) | z +1+ i |=2; г) | z - i |£2;
д) | z +(2-3 i)|³2; е) | z -1- i |<3; ж) 2<| z |<4; з) 1£| z +2 i |<3;
и) | z -2|+| z +2|=5; к) | z +1|+| z -1|=4; л) | z +2|-| z -2|=3; м) | z +1|-| z -1|=4;
н) arg z =  ; о) arg z =
; о) arg z =  ; п) |Re z |³1; р) |Im z |=2;
; п) |Re z |³1; р) |Im z |=2;
с) |Re z |<2; т) |Im z |£3.
 |


Решение. б) Пусть z = x + yi, где x =Re z и y =Im z. Тогда z -(2+3 i)=(x -2)+(y -3) i и | z -(2+3 i)|=  . Поэтому | z -(2+3 i)|=1 Û
. Поэтому | z -(2+3 i)|=1 Û  =1 Û
=1 Û  =1. Получили уравнение окружности с центром (2; 3) и радиусом R =1. Следовательно, множество точек, соответствующее комплексным числам z, удовлетворяющим заданному условию ¾ окружность с центром (2; 3) радиуса R =1 (рис. 2).
=1. Получили уравнение окружности с центром (2; 3) и радиусом R =1. Следовательно, множество точек, соответствующее комплексным числам z, удовлетворяющим заданному условию ¾ окружность с центром (2; 3) радиуса R =1 (рис. 2).
в) Аналогично предыдущему, если z = x + yi, то | z - i |=  и | z - i |£2 Û
и | z - i |£2 Û  £2 Û
£2 Û  £4 ¾ круг с центром (0; 1) радиуса 2 (рис. 3).
£4 ¾ круг с центром (0; 1) радиуса 2 (рис. 3).
 2.2. Геометрический смысл сложения и вычитания комплексных чисел. Пусть a = a + bi и b = c + di ¾ произвольные комплексные числа. Тогда их сумма a + b =(a + c)+(b + d) i изображается вектором с координатами (a + c, b + d), то есть при сложении комплексных чисел они складываются как вектора. В этом заключается геометрический смысл сложения комплексных чисел (рис. 4).
2.2. Геометрический смысл сложения и вычитания комплексных чисел. Пусть a = a + bi и b = c + di ¾ произвольные комплексные числа. Тогда их сумма a + b =(a + c)+(b + d) i изображается вектором с координатами (a + c, b + d), то есть при сложении комплексных чисел они складываются как вектора. В этом заключается геометрический смысл сложения комплексных чисел (рис. 4).
Аналогично, a - b =(a - c)+(b - d) i изображается вектором с координатами (a - c, b - d), и при вычитании комплексных чисел они вычитаются как вектора. В этом заключается геометрический смысл сложения комплексных чисел.
Отсюда вытекают следующие свойства модулей комплексных чисел:
| a |-| b |£| a + b |£| a |+| b |, (2.2.1)
| a |-| b |£| a - b |£| a |+| b |, (2.2.2)
|- a |=| a |.
2.3. Тригонометрическая форма комплексного числа. Пусть a = a + bi ¾ комплексное число с модулем r =| a | и аргументом Arg a. Тогда из геометрических соображений имеем a = r cos j и b = r sin j, откуда
a + bi = r (cos j + i sin j). (2.3.1)
Правая часть полученного равенства (2.3.1) называется тригонометрической формой комплексного числаa + bi.
Таким образом, для нахождения тригонометрической формы комплексного числа a + bi достаточно найти модуль r по формуле
r =  (2.3.2)
(2.3.2)
и аргумент Arg a = j из системы уравнений
 (2.3.3)
(2.3.3)
При этом в качестве аргумента Arg a берётся, как правило, главное значение arg a Î(- p, p ].
2.3.1. Упражнение. Представить в тригонометрической форме комплексное число:
а) 1; б) -4; в) i; г) -2 i; д) 1+ i; е) 1- i;
ж) 3+3 i; з) 1+  i; и)
i; и)  - i; к) -1-
- i; к) -1-  i.
i.
Решение. б) Комплексное число -4 представляется вектором с координатами (-4; 0). Поэтому |-4|=4 и arg(-4)= p. Следовательно, -4=4(cos p + i sin p) ¾ тригонометрическая форма числа -4.
з) Имеем a =1 и b =  . Поэтому |1+
. Поэтому |1+  i |=
i |=  =2. Далее, cos j =
=2. Далее, cos j =  и sin j =
и sin j =  , откуда j =arg(1+
, откуда j =arg(1+  i)=
i)=  и 1+
и 1+  i =2(cos
i =2(cos  + i sin
+ i sin  ).
).
Ответ: б) -4=4(cos p + i sin p);
з) 1+  i =2(cos
i =2(cos  + i sin
+ i sin  ).
).
2.3.2. Теорема. Пусть комплексные числа a и b = a + bi записаны в тригонометрической форме: a = r 1(cos j 1+ i sin j 1), b = r 2(cos j 2+ i sin j 2). Тогда
ab = r 1 r 2[cos(j 1+ j 2)+ i sin(j 1+ j 2)], (2.3.4)
 =
=  [cos(j 1- j 2)+ i sin(j 1- j 2)]. (2.3.5)
[cos(j 1- j 2)+ i sin(j 1- j 2)]. (2.3.5)
Допуская вольность речи, эту теорему формулируют следующим образом: при перемножении комплексных чисел их модули перемножаются, а аргументы складываются; при делении ¾ модули делятся, аргументы вычитаются.
2.3.4. Следствие. Если a = r (cos j + i sin j), то для любого целого числа n имеет место равенство
an = r n (cos nj + i sin nj). (2.3.6)
Формула (2.3.6) носит название формулы Муавра.
2.3.5. Упражнение. Найти значения выражений:
а) (1+ i)20; б) (1- i)100; в) (1+  i)300; г)
i)300; г)  ; д)
; д)  ; е)
; е) 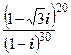 +
+  .
.
Решение. а) Представим 1+ i в тригонометрической форме: 1+ i = 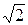 (cos
(cos  + i sin
+ i sin  ). Теперь, по формуле Муавра (2.3.6) получаем
). Теперь, по формуле Муавра (2.3.6) получаем
(1+ i)20=(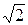 (cos
(cos  + i sin
+ i sin  ))20=(
))20=(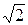 )20(cos 20×
)20(cos 20×  + i sin 20×
+ i sin 20×  )=
)=
=210(cos 5 p + i sin 5 p)=210(cos p + i sin p)= -210.
г) Представим  в тригонометрической форме. Имеем 1+
в тригонометрической форме. Имеем 1+  i =2(cos
i =2(cos  + i sin
+ i sin  ) (см. предыдущее упражнение) и 1- i =
) (см. предыдущее упражнение) и 1- i = 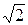 (cos
(cos  + i sin
+ i sin  ). Поэтому
). Поэтому
 =
= 
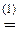
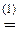
 (cos
(cos 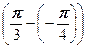 + i sin
+ i sin 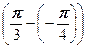 )=
)= 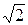 (cos
(cos  + i sin
+ i sin  ).
).
Теперь по формуле Муавра получаем
 =(
=(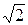 )15(cos 15×
)15(cos 15×  + i sin 15×
+ i sin 15×  )=
)=  (cos
(cos  + i sin
+ i sin  )=
)=
=  (cos
(cos 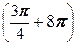 + i sin
+ i sin 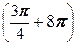 )=
)=  (cos
(cos 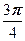 + i sin
+ i sin 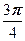 )=
)=
=  (-
(-  +
+  i)=
i)=  ×
×  (-1+ i)=27(-1+ i).
(-1+ i)=27(-1+ i).
á(1) Применяем формулу (2.3.5)ñ
Ответ: а) -210; б) 27(-1+ i).