Лекция
Тема: Производная функции
План лекции:
1. Определение производной функции
2. Правила и формулы дифференцирования
3. Производные основных элементарных функций
4. Производная сложной функции
Понятие производной.
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом 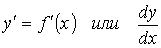 .
.
Тот процесс, с помощью которого из данной функции f(x) получают новую функцию f ' (x), называют дифференцированием и состоит он из следующих трех шагов:
1) даем аргументу x приращение x D и определяем соответствующее приращение функции x) -f(x) Dy = f(x+ D;
2) составляем отношение: 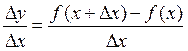 ;
;
3) считая x постоянным, а x D ¦0, находим 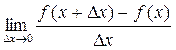 ,который обозначаем через f ' (x), как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения x, при котором мы переходим к пределу.
,который обозначаем через f ' (x), как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения x, при котором мы переходим к пределу.
Определение: Производной y ' =f ' (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен.
Таким образом, 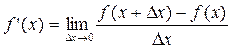 , или
, или 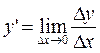 .
.
Заметим, что если при некотором значении x, например при x=a, отношение 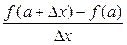 при x D¦0 не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a.
при x D¦0 не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a.
Таблица производных.
| (C)’= 0 С=const | 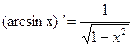
|
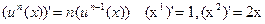
| 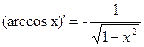
|
| (cos x)'=-sin x | 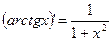
|
| (sin x)'=cos x | 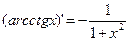
|
(tg x)'= 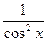
| (ах)'=аx ln a |
(ctg x)'=- 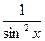
| (ех)'=ex |
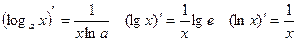
|
Правила дифференцирования.
Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1. d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv
2. d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv
3. d(Cu) = Cdu
4. 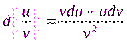
Пример 1
Найти производную функции y = x 2 − 5 x.
Решение.
Применяя линейные правила дифференцирования, получаем:
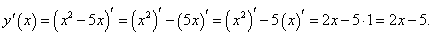
Пример 2
Найти производную функции 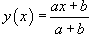 , где a и b - константы.
, где a и b - константы.
Решение.
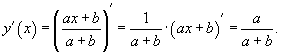
Пример 3
Найти производную функции 2√ x − 3sin x.
Решение.
Используя простейшие правила дифференцирования, получаем:
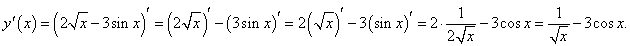
Пример 4
Найти производную функции y = 3sin x + 2cos x.
Решение.
Данное выражение представляет собой линейную комбинацию двух тригонометрических функций. Производная имеет следующий вид:
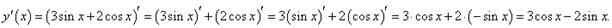
Пример 5
Найти производную функции
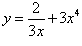 Решение
Решение
Применяя линейные свойства производной, получаем следующий ответ:
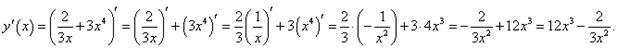
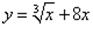 Пример 6 Найти производную функции
Пример 6 Найти производную функции
Решение
Используя приведенные выше формулы дифференцирования, имеем:
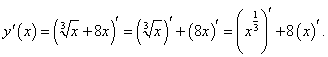
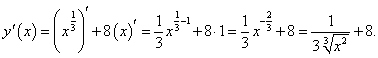
Пример 7
Вычислить производную следующей функции
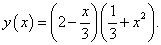
Решение
Чтобы решить данный пример с помощью рассмотренных выше правил дифференцирования, перемножим обе скобки и запишем функцию в таком виде:
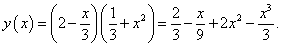
Теперь легко найти производную:
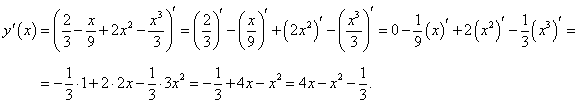
Пример 8Найти производную функции 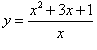 , не используя формулу производной частного.
, не используя формулу производной частного.
Решение
Разделив числитель на знаменатель почленно, запишем функцию в виде
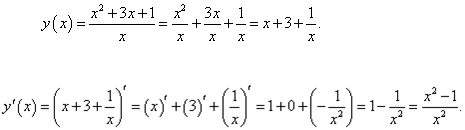 |
Далее, применяя линейные свойства производной, находим:
Производная сложной функции.
Инвариантная форма записи дифференциала.
Пусть y = f(x), x = g(t), т.е у- сложная функция.
Тогда dy = f¢(x)g¢(t)dt = f¢(x)dx.
Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
Однако, если х- независимая переменная, то
dx = Dx, но
если х зависит от t, то Dх ¹ dx.
Таким образом форма записи dy = f¢(x)Dx не является инвариантной.
Пример 9. Найти производную функции 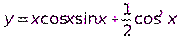 .
.
Сначала преобразуем данную функцию: 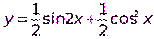
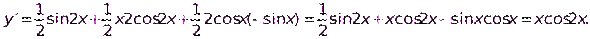
Пример10. Найти производную функции 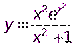 .
.

Пример. Найти производную функции 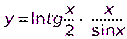
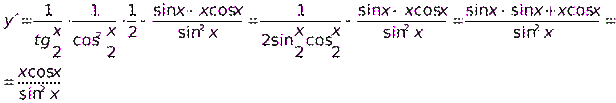
Контрольные вопросы:
1. Что такое производная функции?
2. В чем состоит геометрический смысл производной?
3. В чем состоит физический смысл производной?
4. Каковы основные правила дифференцирования?
5. Перечислите несколько производных элементарных функций?
Литература: [1], c. 172-179