Работа может быть оформлена в тетради или на стандартных листах формата А4. Работа должна иметь титульный лист, на котором указываются: название дисциплины, фамилия, имя и отчество студента, шифр, специальность и курс. На каждой странице необходимо оставлять поля для замечаний рецензента.
Теоретические вопросы должны быть изложены в объеме, достаточном для отражения сути поставленного вопроса и содержать ссылки на используемую литературу.
Все расчеты, выполненные студентом в практической части контрольной работы должны содержать комментарии и выводы по полученным результатам.
В конце работы должен быть помещен список используемой литературы.
Вопросы к теоретической части контрольной работы
Теоретические вопросы по каждой теме выбираются из списка вопросов для самоконтроля. В таблице 1 указаны номера вопросов, соответствующих каждому варианту.
Таблица 1. Варианты вопросов к теоретической части
| Вариант | ||||||||||
| Тема 1. Вопрос | ||||||||||
| Тема 2. Вопрос | ||||||||||
| Тема 3. Вопрос | ||||||||||
| Тема 3. Вопрос | ||||||||||
| Тема 4. Вопрос | - | - | - | - | - | |||||
| Тема 5. Вопрос | - | - | - | - | - | |||||
| Тема 6. Вопрос | - | - | - | - | - | |||||
| Тема 7. Вопрос | - | - | - | - | - |
Задание 1. Используя интерполяционный полином Ньютона вычислить значение функции при указанном значении аргумента х. Используя интерполяционный полином Лагранжа четвёртого порядка вычислить значение функции при указанном значении аргумента х. Подобрать методом наименьших квадратов многочлен наименьшей степени, наилучшим образом, описывающий функцию, заданную таблично и вычислить её значение при заданном значении аргумента.
| X | Y1 | Y2 | Y3 | Y4 | Y5 |
| 0,1 | 0,83550 | 1,46355 | 1,56320 | 1,48342 | 0,73420 |
| 0,3 | -0,35750 | 0,23275 | 1,10440 | 0,88222 | -0,49260 |
| 0,5 | -0,96250 | -1,98125 | 0,30000 | 0,03750 | -1,22500 |
| 0,7 | -0,81150 | -4,70805 | -0,64840 | -0,68018 | -1,35740 |
| 0,9 | 0,26350 | -7,34285 | -1,53920 | -0,81578 | -0,78420 |
| 1,1 | 2,43050 | -9,14645 | -2,17080 | 0,17022 | 0,60020 |
| 1,3 | 5,85750 | -9,24525 | -2,34160 | 2,90182 | 2,90140 |
| 1,5 | 10,71250 | -6,63125 | -1,85000 | 8,08750 | 6,22500 |
| 1,7 | 17,16350 | -0,16205 | -0,49440 | 16,52022 | 10,67660 |
| 1,9 | 25,37850 | 11,43915 | 1,92680 | 29,07742 | 16,36180 |
| x=0,4 | x=1,8 | x=0,6 | x=1,4 | x=0,2 | |
| Y6 | Y7 | Y8 | Y9 | Y0 | |
| 0,2 | 0,17600 | 0,99520 | 1,38960 | 1,23312 | 0,06560 |
| 0,4 | -0,74400 | -0,77760 | 0,73280 | 0,46912 | -0,92720 |
| 0,6 | -0,99200 | -3,31520 | -0,16880 | -0,36368 | -1,37280 |
| 0,8 | -0,40000 | -6,08000 | -1,11360 | -0,85248 | -1,16560 |
| 1,0 | 1,20000 | -8,40000 | -1,90000 | -0,50000 | -0,20000 |
| 1,2 | 3,97600 | -9,46880 | -2,32640 | 1,27552 | 1,62960 |
| 1,4 | 8,09600 | -8,34560 | -2,19120 | 5,14032 | 4,42880 |
| 1,6 | 13,72800 | -3,95520 | -1,29280 | 11,84512 | 8,30320 |
| 1,8 | 21,04000 | 4,91200 | 0,57040 | 22,22512 | 13,35840 |
| 2,0 | 30,20000 | 19,60000 | 3,60000 | 37,20000 | 19,70000 |
| x=1,7 | x=0,5 | x=1,5 | x=0,3 | x=1,1 |
Пример 1. Дана функция y=f(x)
| х | 0,1 | 0,5 | 0,9 | 1,3 | 1,7 |
| у | -0,6575 | -0,0875 | 1,4905 | 5,4205 | 13,0465 |
| х | 2,1 | 2,5 | 2,9 | 3,3 | 3,7 |
| у | 25,7125 | 44,7625 | 71,5405 | 107,3905 | 153,6565 |
Используя интерполяционный полином Ньютона вычислить f(0,8) и f(3,5).
Составим таблицу конечных разностей
| х | у | Δ1у | Δ2у | Δ3у |
| 0,1 | -0,6575 | |||
| 0,5 | -0,0875 | |||
| 0,9 | 1,4905 | |||
| 1,3 | 5,4205 | |||
| 1,7 | 13,0465 | |||
| 2,1 | 25,7125 | |||
| 2,5 | 44,7625 | |||
| 2,9 | 71,5405 | |||
| 3,3 | 107,3905 | |||
| 3,7 | 153,6565 |
Третьи конечные разности постоянны, поэтому при вычислении будем использовать полином Ньютона третьей степени, при этом при вычислении функции при х=0,8 воспользуемся первым полиномом Ньютона
(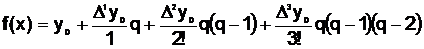 ),
),
а при х=3,5 – вторым
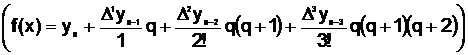 ;
;  , h=0,4.
, h=0,4.
Вычислим f(0,8). Воспользуемся полиномом
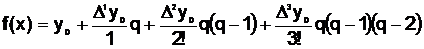 .
.
Пусть х0=0,5, тогда 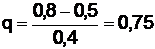 .
.
Имеем 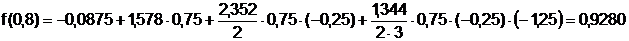 .
.
Вычислим f(3,5). Воспользуемся полиномом
 .
.
xn=3,7,  .
.
Имеем
 Пример 2. Дана функция y=f(x)
Пример 2. Дана функция y=f(x)
| х | 0,25 | 0,30 | 0,65 | 0,70 | 0,85 |
| у | -0,4766 | -0,4145 | 0,3139 | 0,4915 | 1,1922 |
| х | 1,10 | 1,50 | 1,55 | 1,60 | 1,75 |
| у | 3,0775 | 8,6875 | 9,6683 | 10,7200 | 14,3266 |
Используя интерполяционный полином Лагранжа третьего порядка вычислить f(1,3).
Интерполяционный полином Лагранжа третьего порядка имеет вид:
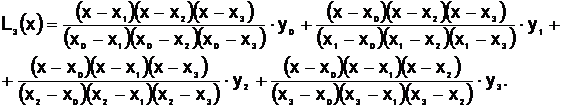
| х | 0,85 | 1,10 | 1,50 | 1,55 |
| у | 1,1922 | 3,0775 | 8,6875 | 9,6683 |
Поэтому выберем четыре точки, например,
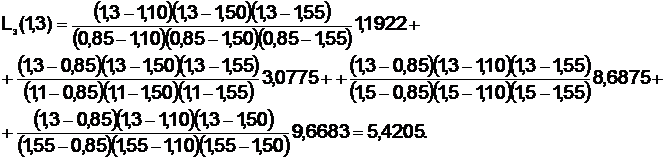
Пример 3. Дана функция y=f(x)
| х | 0,10 | 0,35 | 0,70 | 0,80 | 0,95 |
| у | -0,6575 | -0,3472 | 0,4915 | 0,9280 | 1,8256 |
| х | 1,20 | 1,40 | 1,90 | 2,00 | 2,30 |
| у | 4,1440 | 6,9280 | 18,6655 | 22,0000 | 34,3555 |
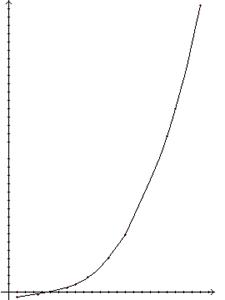
Методом наименьших квадратов подобрать многочлен наилучшим образом описывающий данную функцию (имеющий наименьшую сумму квадратов отклонений).
Пусть искомая функция имеет вид Р(х)=а0+а1х+а2х2+…+amxm. Требуется подобрать многочлен Р(х) так, чтобы S= 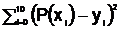 эта сумма была минимальна.
эта сумма была минимальна.
 Для определения коэффициентов аi решаем систему
Для определения коэффициентов аi решаем систему

Из вида графика начальную степень многочлена возьмем равную трем (m=3). Вычисляем значения коэффициентов системы и свободных членов.
Σхi=11,7, Σхi2=18,465, Σхi3=33,25425, Σхi4=64,4107125, хi5=130,2657731, Σхi6=270,7140142; Σyi=88,3334, Σyi xi=175,7876, Σyi xi2=359,102542,
Σyi xi3=750,3946976.
Получаем систему:

Решаем эту систему и находим, что а0=-0,8000; а1=1,6000; а2=-2,1000; а3=3,5000.
Получаем Р3(х)=3,5х3 – 2,1х2 +1,6х – 0,8. При этом S=1,5625Е-9.
Для сравнения возьмем многочлен четвёртой степени. Вычислим дополнительно
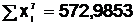 ,
, 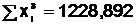 ,
,  .
.
Система для определения коэффициентов:

Её решение а0=-0,8007; а1=1,6049; а2=-2,1082; а3=3,5048; а4=-0,0009.
Получаем многочлен
Р4(х)=-0,0009х4+3,5048х3 – 2,1082х2 +1,6049х – 0,8007.
Вычислим сумму квадратов отклонений
| xi | 0,10 | 0,35 | 0,70 | 0,80 | 0,95 |
| yi | -0,6575 | -0,3472 | 0,4915 | 0,9280 | 1,8256 |
| P4(xi) | -0,65776 | -0,34696 | 0,491682 | 0,928104 | 1,825546 |
| (уi -P(xi))2 | 7,074E-8 | 5,864E-8 | 3,299E-8 | 1,076E-8 | 2,955E-9 |
| xi | 1,20 | 1,40 | 1,90 | 2,00 | 2,30 |
| yi | 4,1440 | 6,9280 | 18,6655 | 22,0000 | 34,3555 |
| P4(xi) | 4,143843 | 6,927827 | 18,66557 | 22,00011 | 34,35545 |
| (уi -P(xi))2 | 2,462E-8 | 2,995E-8 | 4,840E-9 | 1,132E-8 | 2,828E-9 |
S=2,496E-7.
Сравнивая отклонения, замечаем, что отклонение для многочлена третьей степени меньше, чем для четвёртой.
Замечание. Сравнивая коэффициенты этих многочленов, видим, что старший коэффициент многочлена четвертой степени практически равен нулю.
Итак, многочленом наилучшим образом описывающий данную функцию, является многочлен третьей степени Р3(х)=3,5х3 – 2,1х2 +1,6х – 0,8.
Задание 2. Определить начальные значения корней уравнения (в том числе и начальные значения близких корней) и уточнить один из них с точностью e=0,0001 методом Бриге-Виетта, усовершенственным методом последовательных приближений и комбинированным методом.
| Bариант | уравнение | Bариант | уравнение |
| 2х3-5х2+4х-1,005=0; | 3х3-4х2-х+1,96=0; | ||
| 3х3-7х2+5х-1,006=0; | 4х3-5х2-2х+2,98=0; | ||
| 3х3-8х2+7х-2,005=0; | 2х3+7х2+8х+2,99=0; | ||
| 4х3-9х2+6х-1,007=0; | 2х3-х2-4х+2,98=0; | ||
| 4х3-11х2+10х-3,008=0; | 2х3+х2-4х-2,98=0. |
Пример. Выполним данное задание для уравнения
3х3 – 5,6х2 +1,43х +1,207.
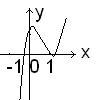 Схематично график функции у= 3х3 – 5,6х2 +1,43х +1,207 представлен на рисунке. На этом рисунке видим, что данное уравнение имеет один отрицательный корень и два положительных близких. За начальное значение отрицательного корня можно взять х1= - 0,5. Для нахождения начальных значений близких корней предварительно решим уравнение
Схематично график функции у= 3х3 – 5,6х2 +1,43х +1,207 представлен на рисунке. На этом рисунке видим, что данное уравнение имеет один отрицательный корень и два положительных близких. За начальное значение отрицательного корня можно взять х1= - 0,5. Для нахождения начальных значений близких корней предварительно решим уравнение
(3х3 – 5,6х2 +1,43х +1,207)’=0. Продифференцируем левую часть равенств, получим 9х2–11,2х+1,43=0. Решением этого квадратного уравнения будут значения 0,14444 и 1,1. Из графика видно, что близкие корни лежат в окрестности х=1,1. Вычислим d, которое определяет отклонение начальных значений от 1,1. 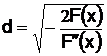 .
.
В нашем примере F(x)= 3х3 – 5,6х2 +1,43х +1,207 и его значение F(1,1)=-0,003. F″(x)=18x – 11,2 и F″(1,1)=8,6. Тогда 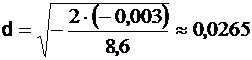 . Начальное значение х2 возьмём равным 1,0735, а х3 = 1,1265.
. Начальное значение х2 возьмём равным 1,0735, а х3 = 1,1265.
Уточним корень х1= – 0,5 методом Бриге-Виетта.
Рекуррентная формула метода  . b и c определяются соотношениями:
. b и c определяются соотношениями:
b3=a3, c3=b3;
b2=a2 + xn*b3, c2=b2 + xn*c3;
b1=a1 + xn*b2, c1=b1 + xn*c2;
b0=a1 + x0*b1.
| x0=-0,5 | |||
| i | a | b | c |
| -5,6 | -7,1 | -8,6 | |
| 1,43 | 4,98 | 9,28 | |
| 1,207 | -1,283 | ||
| x1=-0,36175 | |||
| i | a | b | c |
| -5,6 | -6,685237069 | -7,770474138 | |
| 1,43 | 3,848355694 | 6,65929122 | |
| 1,207 | -0,185126085 | ||
| x2=-0,33395 | |||
| i | a | b | c |
| -5,6 | -6,601838065 | -7,60367613 | |
| 1,43 | 3,634657558 | 6,173874952 | |
| 1,207 | -0,006779432 | ||
| x3=-0,33285 | |||
| i | a | b | c |
| -5,6 | -6,598543814 | -7,597087628 | |
| 1,43 | 3,626311702 | 6,154986654 | |
| 1,207 | -1,03725E-05 | ||
| x4=-0,33285 |
Уточним этот же корень комбинированным методом. При уточнении корня на отрезке [a, b] касательная проводится из точки, в которой знак функции совпадает со знаком второй производной. В нашем примере это условие выполняется при х=а, поэтому новое значение  ,
, 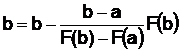 . Применительно к данному примеру а=–0,5, b=0,
. Применительно к данному примеру а=–0,5, b=0,
F(x)= 3х3 – 5,6х2 +1,43х +1,207, F¢(x)= 9х2–11,2х+1,43.
Результаты расчётов сведём в таблицу
| i | ai | bi |
| -0,5 | ||
| -0,36175 | -0,24237 | |
| -0,33395 | -0,32895 | |
| -0,33285 | -0,33284 | |
| -0,33285 | -0,33285 |
Уточним первый корень х1= – 0,5 усовершенственным методом последовательных приближений. Рекуррентная формула имеет вид для уравнения x=f(x):  . Преобразуем исходное уравнение к виду x=f(x), например, х=х – 0,2(3х3 – 5,6х2 +1,43х +1,207) или х= – 0,6х3+1,12х2+0,714х – 0,2414. х0=–0,5 определим значение х1 используя формулу последовательных приближений
. Преобразуем исходное уравнение к виду x=f(x), например, х=х – 0,2(3х3 – 5,6х2 +1,43х +1,207) или х= – 0,6х3+1,12х2+0,714х – 0,2414. х0=–0,5 определим значение х1 используя формулу последовательных приближений
х1 = – 0,6х03+1,12 х02+0,714 х0 – 0,2414, вычисляя, получаем х1=–0,2434.
Результаты вычисления по усовершенственному методу последовательных приближений занесём в таблицу
| i | xi | x i+1 |
| –0,5 | –0,2434 | |
| –0,2434 | –0,31368 | |
| –0,31368 | –0,34780 | |
| –0,34780 | –0,33568 | |
| –0,33568 | –0,33075 | |
| –0,33075 | –0,33244 | |
| –0,33244 | –0,33315 | |
| –0,33315 | –0,33290 | |
| –0,33290 | –0,33280 | |
| –0,33280 | –0,33284 | |
| –0,33284 | –0,33285 | |
| –0,33285 | –0,33285 |
Итак, в качестве приближенного значения первого корня с точностью 0,0001 возьмём –0,3328.
Методы Бриге-Виетта и комбинированный методы достигли точности за четыре итерации.
Уточняя второй корень методом Бриге-Виетта, находим х2=1,0733 и х3=1,1262.
Задание 3. Решить систему линейных уравнений методом Гаусса и методом Гаусса -Зейделя.
a1x+b1y+c1z=d1,
a2x+b2y+c2z=d2,
a3x+b3y+c3z=d3.
| вариант | ak | bk | ck | dk | |
| 2.8500 | -1.1200 | 4.3700 | 15.1720 | ||
| 13.1000 | 4.0800 | 15.2400 | 54.4380 | ||
| 5.2200 | 2.1400 | -3.0600 | 0.4554 | ||
| 13.1000 | 4.0800 | 15.2400 | 54.4380 | ||
| 5.2200 | 2.1400 | -3.0600 | 0.4554 | ||
| 4,5500 | 7,4400 | 2,1300 | 8,9220 | ||
| 14,9900 | 11,7200 | -3,9900 | 9,8328 | ||
| 2.8500 | -1.1200 | 4.3700 | 15.1720 | ||
| 5.2200 | 2.1400 | -3.0600 | 0.4554 |
| вариант | ak | bk | ck | dk | |
| 4,5500 | 7,4400 | 2,1300 | 8,9220 | ||
| 14,9900 | 11,7200 | -3,9900 | 9,8328 | ||
| 2.8500 | -1.1200 | 4.3700 | 15.1720 | ||
| 2.8500 | -1.1200 | 4.3700 | 15.1720 | ||
| 5.2200 | 2.1400 | -3.0600 | 0.4554 | ||
| 20,0200 | 14,7800 | 9,9400 | 48,6434 | ||
| 2.8500 | -1.1200 | 4.3700 | 15.1720 | ||
| 4,5500 | 7,4400 | 2,1300 | 8,9220 | ||
| 20,0200 | 14,7800 | 9,9400 | 48,6434 | ||
| 4,5500 | 7,4400 | 2,1300 | 8,9220 | ||
| 20,0200 | 14,7800 | 9,9400 | 48,6434 | ||
| 5.2200 | 2.1400 | -3.0600 | 0.4554 | ||
| 9,2200 | -8,6600 | 7,9200 | 37,0494 | ||
| 2.8500 | -1.1200 | 4.3700 | 15.1720 | ||
| 5.2200 | 2.1400 | -3.0600 | 0.4554 | ||
| 2.8500 | -1.1200 | 4.3700 | 15.1720 | ||
| 4,5500 | 7,4400 | 2,1300 | 8,9220 | ||
| 9,2200 | -8,6600 | 7,9200 | 37,0494 | ||
| 9,2200 | -8,6600 | 7,9200 | 37,0494 | ||
| 5.2200 | 2.1400 | -3.0600 | 0.4554 | ||
| 4,5500 | 7,4400 | 2,1300 | 8,9220 |
Пример. Решить систему линейных уравнений методом Гаусса.

Выпишем матрицу коэффициентов системы.
10,000000 11,700000 18,465000 33,254250 88,333400
11,700000 18,465000 33,254250 64,410710 175,787600
18,465000 33,254250 64,410710 130,265770 359,102500
33,254250 64,410710 130,265770 270,714010 750,394700
Вычислим m1= 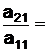 1,17; m2=
1,17; m2=  1,8465; m2=
1,8465; m2= 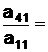 3,325425.
3,325425.
Исключаем а0 из второго, третьего и четвёртого уравнений для чего последовательно умножаем коэффициенты первого уравнения на (-m1) и складываем с коэффициентами второго, затем умножаем коэффициенты первого уравнения на (-m2) и складываем с коэффициентами третьего и т.д. и получаем:
10,0000 11,700000 18,465000 33,254250 88,333400
0,0000 4,776000 11,650200 25,503238 72,437522
0,0000 11,650200 30,315088 68,861797 195,994877
0,0000 25,503238 68,861797 160,129496 456,648603
m1= 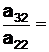 2,439322 m2=
2,439322 m2= 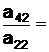 5,339874.
5,339874.
Исключаем а1 из третьего и четвёртого уравнений и получаем
10,0000 11,700 18,465000 33,254250 88,333400
0,0000 4,7760 11,650200 25,503238 72,437522
0,0000 0,0000 1,8965029 26,651199 19,29646425
0,0000 0,0000 6,651199066 23,945425 69,84137393
m1= 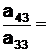 3,507086
3,507086
Исключаем а2 из четвёртого уравнения и получаем
10,0000 11,70000 18,465000 33,254250 88,333400
0,0000 4,776000 11,650200 25,503238 72,437522
0,0000 0,00000 1,8965029 26,651199 19,296464
0,0000 0,00000 0,0000 0,6190966 2,1670114
Из последнего уравнения вычисляем а3= 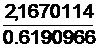 =3,500 подставляем это значение в третье уравнение, из которого определяем а2= -2,1, далее определяем а1=1,6 и а0=-0,8.
=3,500 подставляем это значение в третье уравнение, из которого определяем а2= -2,1, далее определяем а1=1,6 и а0=-0,8.
Решим эту систему методом Гаусса –Зейделя.
Матрица коэффициентов системы симметрична и положительно определенная, поэтому попытаемся решить её методом Гаусса –Зейделя, выразив аi из соответствующих уравнений.
а0=(88,333400 – (11,7а1+18,465а2+33,25425а3))/10,
а1=(175,7876 – (11,7а0+33,25425а2+64,41071а3))/18,465,
а2=(359,1025 – (18,465а0+33,25425а1+130,26577а3))/64,41071,
а3=(750,3947 – (33,25425а0+64,41071а1+130,26577а2))/270,71401.
Количество итераций, которое потребовалось для достижения результата составило более 9100. Таблица начальных значений и последних значений итераций представлена ниже.
| i | a0 | a1 | a2 | a3 |
| 0,00000000 | 0,00000000 | 0,000000000 | 0,00000000 | |
| 8,83334000 | 3,92296355 | 1,017527461 | 0,26381619 | |
| 1,48730725 | 5,82487976 | 1,607980183 | 0,42955293 | |
| -2,37935077 | 6,63341565 | 1,963833449 | 0,54092116 | |
| -4,35276753 | 6,85448446 | 2,190196335 | 0,62181081 | |
| -5,29838955 | 6,76383134 | 2,344493037 | 0,68529257 | |
| -5,68833813 | 6,51159584 | 2,458120126 | 0,73853103 | |
| -5,78007549 | 6,17937905 | 2,548266665 | 0,78546605 | |
| -5,71391632 | 5,81138903 | 2,624365447 | 0,82827639 | |
| -5,56624697 | 5,43143864 | 2,691614020 | 0,86817847 | |
| -0,79999990 | 1,60001628 | -2,100016596 | 3,50000427 | |
| -0,80000010 | 1,60001722 | -2,100017561 | 3,50000453 |
Задание 4. Решить систему нелинейных уравнений:
0. 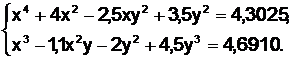 1.
1. 
2. 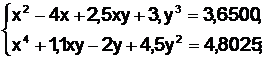 3.
3. 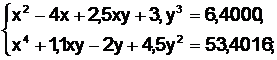
4. 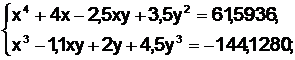 5.
5. 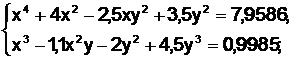 6.
6. 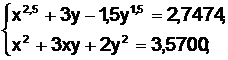 7.
7. 
8.  9.
9. 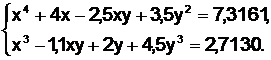
Пример. Решить систему нелинейных уравнений
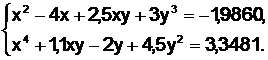
Решение. Будем решать систему методом Ньютона.
Пусть F(x,y)= x2–4x+2,5xy+3y3+1,9860, G(x,y)=x4+1,1xy–2y+4,5y2–,3481.
Частные производные этих функций: Fx=2x – 4+2,5y, Fy=2,5x+9y2, Gx=4x3+1,1y, Gy=1,1x – 2+9y, J(x,y)=FxGy – FyGx,
xn+1=xn – (F(xn,yn)*Gy – Fy*G)/J(xn,yn), yn+1=yn+(F*Gx – Fx*G)/ J(xn,yn). При начальных значениях (1; 2) производим расчёт, результаты которого сводим в таблицу.
| n | x | y | F | Fx | Fy |
| 1,35 | -0,68 | 0,000796 | -3 | 7,5366 | |
| 1,348589 | -0,11953 | 0,956478 | -1,60164 | 3,500052 | |
| 1,558106 | 0,493453 | 2,686939 | 0,349845 | 6,086729 | |
| 1,605405 | 0,439199 | 2,594277 | 0,308807 | 5,749573 | |
| 1,606248 | 0,39016 | 2,4736 | 0,187898 | 5,385647 | |
| 1,6062 | 0,358147 | 2,3854 | 0,107768 | 5,169925 | |
| ... | ... | ... | ... | ... | |
| 1,601372 | 0,318902 | 2,268311 | 2,78E-08 | 4,918718 | |
| 1,601372 | 0,318902 | 2,268311 | 1,22E-08 | 4,918718 |
| n | G | Gx | Gy | J | FGy-GFy | FGx-GFx |
| 0,008406 | 9,0935 | -6,635 | -48,6291 | -0,06864 | -27,2553 | |
| -2,31043 | 9,679185 | -1,5923 | -31,3274 | 6,56363 | -19,2031 | |
| 1,104164 | 15,67322 | 4,154995 | -93,945 | 4,443474 | 5,096911 | |
| 1,663735 | 17,03371 | 3,718736 | -96,7882 | 0,081666 | 4,746354 | |
| 1,506533 | 17,00588 | 3,278317 | -90,9717 | -0,00441 | 2,912295 | |
| 1,405373 | 16,96917 | 2,990145 | -87,4071 | -0,13298 | 1,677279 | |
| ... | ... | ... | ... | ... | ... | |
| 1,2136 | 16,77698 | 2,63163 | -82,5213 | -1E-07 | 4,32E-07 | |
| 1,2136 | 16,77698 | 2,63163 | -82,5213 | -4,5E-08 | 1,9E-07 |
Задание 5. Построить решение дифференциального уравнения на заданном промежутке методами Эйлера второго порядка (исправленным – И, модифицированным – М):
0.  М
М
1. y’cosx- ysinx =sin2x, y(0)=2 [0;1] И
2.  М
М
3.  И
И
4.  М
М
5.  И
И
6.  М
М
7.  И
И
8.  М
М
9.  И
И
Задание на курсовую работу
На промежутке [0; 2] решить дифференциальное уравнение 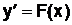 у(0)=у0 (обосновав выбор шага интегрирования). Подобрать многочлен Рn(х) наилучшим способом, описывающий полученное решение. Определить корни уравнения Рn(х)=f(x) с точностью 0,0001.
у(0)=у0 (обосновав выбор шага интегрирования). Подобрать многочлен Рn(х) наилучшим способом, описывающий полученное решение. Определить корни уравнения Рn(х)=f(x) с точностью 0,0001.
| вариант | F(x) | y(0) | f(x) |
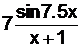
| x+11.75 | ||
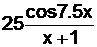
| 1.5x+13.2 | ||
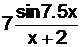
| 0.6x+15.2 | ||

| 20-1.2x | ||
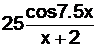
| 17-1.5x | ||
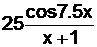
| 14.5 | ||

| |||

| 30-1.2x | ||
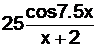
| 1.5x+13 | ||
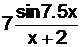
| 4.6x+19.7 |
Указание к выполнению.
1. Решить дифференциальное уравнение, обосновав выбор шага интегрирования.
2. Выбрать узлы интерполяции и подобрать многочлен.
3. Определить значения корней многочлена на заданном интервале.