Основные понятия и модели пористых сред.
Пористую среду представляют, как множество твердых частиц, плотно прилегающих друг к другу, пространство между которыми может быть заполнено жидкостью или газом.
Под пористостью горной породы понимают наличие в ней пустот различной формы и происхождения. Количественно величина пористости определяется коэффициентом пористости m, определяемым для некоторого элемента пористой среды, как отношением объема пор 
в этом элементе к его общему объему 
(измеряется в долях или процентах):
(1.1)
Различают общую mобщ, открытую mоткр и динамическую (эффективную) mэфф пористость:
; 
; 
(1.2)
где: 
- объем всех пор; 
- объем сообщающихся пор; 
- часть объема открытых пор, через которые может фильтроваться жидкость.
Коэффициент открытой пористости можно определить методом взвешивания, при котором определяются: масса сухого образца М1, масса образца, на 100 % насыщенного водой М2 и масса образца, на 100% насыщенного водой во взвешенном состоянии в воде М3. Тогда коэффициент открытой пористости равен:
(1.3)
Другой способ (газоволюметрический) определения открытой пористости основан на применении закона Бойля-Мариотта. Идеальный газ из калибровочного сосуда с известным объемом V0 при известном давлении p0 перетекает в поровое пространство сухого образца объемом Vобр, находящимся в непроницаемой манжете и обжатого со всех сторон «горным» давлением. При этом давление внутри замкнутой системы сосуд – образец устанавливается до значения р. Тогда объем пор определяется из соотношения:
(1.4)
где V* - «мертвый» объем трубок соединяющих калибровочный сосуд с образцом, а коэффициент открытой пористости определяется из соотношения (1.2). Отметим, что в процессе всего эксперимента поддерживается постоянная температура.
Коэффициентом просветности n называется отношение площади просветов Sпросв в данном сечении пористой среды ко всей площади этого сечения S:
(1.5)
Среднее по длине пласта значение просветности равно пористости.
Модель фиктивного грунта состоит из шариков одного диаметра уложенных определенным образом, рис. 1.
Основным элементом фиктивного грунта является ромбоэдр, который получается, если принять центры восьми соприкасающихся частиц за вершины углов.
Пористость m и просветность n ячейки Шлихтера изменяются по закону:
(1.6)
(1.7)
где q - угол, определяющий способ упаковки шариков одинакового размера (600 < q < 900)
Удельная поверхность – это суммарная площадь поверхности частиц, которые содержатся в единице объема пористой среды:
(1.8)
Для фиктивного грунта:
(1.9)
Эффективный диаметр частиц фиктивного грунта 
, при котором его гидравлическое сопротивление совпадает с гидравлическим сопротивлением реального грунта определяется в результате гранулометрического (механического) анализа.
Измельченный грунт просеивают через набор сит с различной площадью отверстий, разделяя и взвешивая фракции. Затем строят кривую механического состава, откладывая по оси абсцисс средние диаметры di фракций, а по оси ординат – сумму масс фракций в процентах от общей массы 
, рис.2.
За средний диаметр каждой фракции принимают среднее арифметическое крайних диаметров d’:
(1.10)
Эффективный диаметр определяют по гранулометрическому составу, н.п. по формуле веса средней частицы
(1.11)
где di - средний диаметр i -ой фракции; ni - массовая или счетная доля i -ой фракции.
Эмпирические способы определения :
По Газену:
при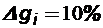 
(1.12)
По методу Крюгера - Цункера:
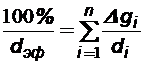(1.13)
Капиллярная модель пористой среды (идеальный грунт) – система прямых трубок малого диаметра одинакового сечения длиной 
.
Для капиллярной модели имеется связь радиуса трубок (пор) с диаметром частиц фиктивного грунта:
(1.14)
Скоростью фильтрации v называется отношение объемного расхода жидкости Q к площади поперечного сечения F, нормального к направлению движения жидкости.
(1.15)
Скорость фильтрации v и истинная (средняя) скорость движения жидкости 
связаны соотношением:
(1.16)
Задачи к разделу 1
Задача 1.1
Вывести формулу Шлихтера для свободной упаковки частиц (q =900) и для более плотной (q =600).
Задача 1.2
Определить коэффициенты пористости и просветности ячейки Шлихтера, если угол укладки частиц a равен 600, 700, 800, 900. Построить график зависимости данных величин от угла укладки.
Задача 1.3
Определите удельную поверхность песка, пористость которого равна 
и эффективный диаметр 
мм, а также найти число частиц в единице объема среды N / V.
Задача 1.4
Вывести формулу (1.9) для удельной поверхности фиктивного грунта.
Задача 1.5
Построить кривую механического анализа и определить эффективный диаметр песчинок по способам Газена и Крюгера-Цункера по следующим гранулометрическим составам:
 ,мм
| 0 - 0.05 | 0.05 - 0.1 | 0.1 - 0.2 | 0.2 - 0.3 | 0.3 - 0.5 | 0.5 - 1 | |
| а) |  %
| 5,3 | 7,2 | 40,1 | 35,7 | 10,2 | 1,5 |
| б) | %
| 6,9 | 38,6 | 44,2 | 6,3 | 3,3 | 0,7 |
| в) | %
| 1,5 | 5,3 | 7,2 | 40,1 | 35,7 | 10,2 |
Задача 1.6
Оценить удельную поверхность образца и число частиц N в образце для свободной упаковки частиц (q = 900), если до измельчения его диаметр d = 2,54 см, а длина L = 3 см. Средний диаметр зерен взять из решений задачи 1.4 методом Крюгера Цункера.
Задача 1.7
Сопоставить число частиц диаметром d, заключенных в 1 м3 фиктивного грунта (N / V), при наиболее свободном расположении частиц (q = 900) и при наиболее плотном их расположении(q = 600).
Задача 1.8
Определить удельную поверхность Sуд фиктивного грунта и радиус пор идеального грунта r, если эффективный диаметр частиц dэф =0,11мм, а угол упаковки q = 750.
Задача 1.9
Определить скорость фильтрации и среднюю скорость движения воды при установившемся потоке через цилиндрический образец диаметром d = 2,54 см, если известно, что расход через образец Q =0,7см3/мин, масса сухого образца М1 = 116,3 г, масса образца, на 100% насыщенного водой М2 = 126,49 г, а масса образца, на 100% насыщенного водой во взвешенном состоянии в воде М3 = 72,03 г. Сжимаемостью образца пренебречь.
Задача 1.10
Определить скорость фильтрации и среднюю скорость движения нефти у стенки гидродинамически совершенной скважины и на расстоянии r = 75 м, если известно, что мощность пласта h = 10 м, коэффициент пористости m = 18%, радиус скважины rс = 0,1 м, массовый дебит скважины Qm = 50 т/сут и плотность нефти r =0,85г/см3. Жидкость считать несжимаемой.