Закон Дарси и границы его применимости.

 

Закон Дарси устанавливает, что объемный расход несжимаемой жидкости Q через трубку с пористой средой прямо пропорционален потере напора и площади фильтрации S и обратно пропорционально длине трубки L, рис.3:

(2.1)

где: С - коэффициент фильтрации, характеризующий скорость потока через единицу площади сечения, перпендикулярного к потоку, под действием единичного градиента давления.

H - напор в любом сечении определяется как:

(2.2)

где: z - высота положения, - пьезометрическая высота, p – гидростатическое давление, r - плотность жидкости, g – ускорение свободного падения, - скоростной напор,

В силу малости скорости фильтрации (ее порядок » 10^-5 - 10^-6 м/с) скоростным напором в формуле (2.2) можно пренебречь.

Поскольку коэффициент фильтрации С характеризует, как свойства породы, так и свойства воды, то при решении задач о течении других жидкостей и газов в пористой среде удобнее пользоваться понятием проницаемости в законе Дарси:

(2.3)

где: k – абсолютная проницаемость пористой среды, характеризующая способность горной породы пропускать сквозь себя жидкость или газ, m - динамическая вязкость, а - приведенное давление.

S

Рис. 3. Схема опыта Дарси.

 

При условии равенства высот положения z₁ = z₂ закон Дарси примет вид:

(2.4)

Закон Дарси в дифференциальной форме:

(2.5)

Коэффициенты фильтрации и проницаемости связаны соотношением:

(2.6)

При больших скоростях фильтрации закон Дарси нарушается вследствие того, что силы инерции, возникающие в жидкости, становятся соизмеримыми с силами трения. Скорость фильтрации (или дебит) при которой(м) происходит такое нарушение закона Дарси называется критической скоростью фильтрации v_кр (критическим дебитом Q_кр).

Критерием выполнимости закона Дарси служит число Рейнольдса Re, которое, как и в трубной гидравлике, характеризует отношение сил инерции к силам вязкости:

(2.7)

где a – характерный размер задачи.

В таблице 1 представлены выражения для определения чисел Рейнольдса, выведенных разными авторами, а также диапазоны критических чисел Рейнольдса Re_кр (при которых происходит нарушение линейного закона Дарси).

 

Таблица 1. Формулы разных авторов для чисел Рейнольдса.

Автор	Число Рейнольдса	Диапазон критических чисел
Н.Н. Павловский		7,5≤ Reкр ≤9
В.Н. Щелкачев		1≤ Reкр ≤12
М.Д. Миллионщиков		0.022≤ Reкр ≤0.29

 

Если в задаче необходимо определить нарушается ли закон Дарси при заданных параметрах, то полученное в ходе решения число Рейнольдса Re сравнивают с нижним значением Re_кр. Если Re < Re_кр, то закон Дарси выполняется, а если Re ≥ Re_кр, то закон Дарси нарушается. При решении обратной задачи, где нужно определить критическую скорость фильтрации или критический дебит при превышении которых нарушается закон Дарси, выбирают одну из формул, указанных в таблице 1, и определенное значение Re_кр, при котором v=v_кр.

При нарушении закона Дарси при больших скоростях фильтрации используют степенные законы:

Формула Форшгеймера (двучленный закон фильтрации):

(2.8)

в диф. форме. (2.9)

где b - дополнительная константа пористой среды, определяемая из эксперимента.

Одночленный степенной закон:

(2.10)

- в диф. форме. (2.11)

где С и n постоянные определяемые опытным путем, причем 1≤ n ≤2.

При n = 2 выражение (2.10) и (2.11) носит название формулы А.А.Краснопольского.

Отклонения от линейного закона Дарси наблюдаются и при малых скоростях фильтрации. Это связано с проявлением неньютоновских свойств фильтрующихся жидкостей, а также других физико-химических эффектов (учет сил межфазного и межмолекулярного взаимодействия).

Для вязкопластичных жидкостей (обладающих, как свойствами жидкости, так и свойствами твёрдого тела) часто используют закон фильтрации с предельным градиентом:

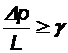, (2.12)

,

В дифференциальной форме:

(2.13)

Из (2.12) следует, что при градиентах меньших предельного g жидкость неподвижна, а при превышении g течет по линейному закону.

Величина g зависит от предельного напряжения сдвига t₀ и среднего диаметра пор:

, где a - безразмерная константа.

Аналогом закона Дарси можно считать закон Пуазейля, если пористую среду представить в виде системы трубок одинакового сечения:

или (2.14)

где N - число трубок одинакового сечения, а r - радиус поровых каналов (или средний радиус пор среды).

Если учесть, что пористость такой среды равна:

, (2.15)

где - число каналов на единицу площади поперечного сечения.

Тогда формулу Пуазейля можно представить в виде:

или (2.16)

 

Задачи к разделу 2

 

Задача 2.1

Из аналогии законов Дарси и Пуазейля найти пористость, проницаемость и удельную поверхность капиллярной модели с плотностью капиллярных каналов n^/ (число каналов на единицу площади поперечного сечения) и радиусом r.

 

Задача 2.2

Определить коэффициент фильтрации, если известно, что площадь поперечного сечения горизонтально расположенного образца песчаника S = 30 см², длина образца L = 15 см, разность давлений на входе жидкости в образец и на выходе Dp = 19,6 кПа, плотность жидкости ρ = 1000 кг/м³ и расход Q = 5 л/час.

 

Задача 2.3

Определить коэффициент пористости, если известно, что скорость движения жидкости через образец, определяемый с помощью индикатора, равна v_ср = 3×10^-2 см/сек, коэффициент проницаемости k =0,2 Д, динамическая вязкость m = 4 мПа×с, а разность давления Dp =2кгс/см² при длине образца L =15 см.

 

Задача 2.4

Определить коэффициенты проницаемости и фильтрации для цилиндрического образца пористой среды диаметром d = 5 см, длиной L = 20 см, если разность давлений на концах образца составляет 300 мм рт.ст., расход жидкости Q = 0,017 л/ч, динамический коэффициент вязкости жидкости μ = 5 мПа·с, плотность её ρ = 0,85 г/см³.

Найти также скорость фильтрации и среднюю скорость движения, если известно, что объем пор составляет V_п =74.6 см³.

 

Задача 2.5

Через два однородных одинаковых образца пористой среды, содержащих глинистые частицы, пропускали:

а) пресную воду при t = 20°C при перепаде давления Dр = 500 мм рт. ст. с расходом Q = 2 см³/мин;

б) соленую воду с удельным весом g = 11030 кг/м²с² и вязкостью m=1,1 сПз при той же разности давления, что и в случае а) и с расходом Q = 0,12 см³/с.

Размер образцов: длина L = 5 см, площадь поперечного сечения F =5см².

Определить коэффициент проницаемости и коэффициент фильтрации в обоих случаях.

Найти отношение проницаемостей для случаев а) и б). Объяснить полученный результат.

 

Задача 2.6

Определить по формуле Щелкачева, происходит ли фильтрация в пласте по закону Дарси, если известно, что дебит нефтяной скважины Q =200 м³/сут проницаемость пласта k = 0,2Д, мощность пласта h = 5м, пористость пласта m =16%, динамический коэффициент вязкости m =5сПз, плотность нефти r =0,8 г/см³, радиус гидродинамически совершенной скважины r_с =0,1 м.

 

Задача 2.7

Определить критический дебит скважины в т/сут (дебит, при превышении которого в призабойной зоне нарушается закон Дарси), если известно, что проницаемость пласта k = 1Д, мощность пласта h =20м, пористость пласта m =18%, динамический коэффициент вязкости m =5 сПз, плотность нефти r = 0,85 г/см³, радиус скважины r_с.

Указание: При определении значения числа Рейнольдса пользоваться формулой Щелкачёва, при Re_кр=1

 

Задача 2.8

Определить скорость фильтрации жидкости через пористую среду при Re_кр = 0,1 (по Миллионщикову). Абсолютная проницаемость среды k =1Д, динамический коэффициент вязкости m = 1 мПа·с, плотность жидкости r = 1000 кг/м³, пористость среды m = 0,2.

 

Задача 2.9

Определить радиус призабойной зоны r_кр, в которой нарушен закон Дарси, при установившейся плоскорадиальной фильтрации нефти, если известно, что массовый дебит скважины Q_m = 210 т/сут, мощность пласта h = 40 м, проницаемость k = 0,6 Д,пористость пласта m = 19%, динамический коэффициент вязкости нефти в пластовых условиях m =18^.10^-3 Па^. с, а ее плотность ρ = 0,75 г/см³.

Указание. В решении использовать число Рейнольдса рассчитанное по формуле М. Д. Миллионщикова при Re_кр = 0,022.