Совершенная скважина вскрывает пласт на всю его мощность и при этом вся поверхность скважины является фильтрующей.
Установившийся одномерный поток жидкости или газа реализуется в том случае, когда давление и скорость фильтрации не изменяются во времени, а являются функциями только одной координаты, взятой вдоль линии тока.
1. Плоскопараллельное течение имеет место в прямоугольном горизонтальном пласте длиной L с постоянной мощностью h. Жидкость движется фронтом от прямолинейного контура питания с давлением рк к галерее скважин (скважины расположены на одной прямой праллельной контуру питания в виде цепочки на одинаковом расстоянии друг от друга) шириной (длиной галереи) В с одинаковым давлением на забоях скважин рг (рис. 4). При такой постановке задачи площадь фильтрации будет постоянной и равна S = B×h, а векторы скорости фильтрации параллельны между собой.
При условии, что в однородном по пористости и проницаемости несжимаемом пласте фильтруется несжимаемая жидкость по закону Дарси, то объемный дебит на добывающей галерее скважин равен:
(3.1)
Давление в любом сечении пласта определяется по формулам:
(3.2)
либо, с учетом (3.1):
(3.3)
Распределение давления в пласте по законам (3.2), (3.3) будет одно и то же, а его вид показан на рисунке 5.
Время, в течение которого отмеченные частицы жидкости пройдут путь х, будет равно:
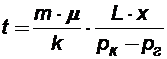(3.4)
2. Плоскорадиальный поток возможен только к гидродинамически совершенной скважине радиусом rс, которая вскрыла пласт мощностью h с круговым контуром питания радиусом Rк, а давления на скважине и контуре питания равны рс и рк соответственно. При таком течении векторы скорости фильтрации направлены по радиусам к оси добывающей скважины, рис.6, а площадь фильтрации S = 2 πrh. Объемный дебит такой скважины определяется по формуле Дюпюи:
|
|
(3.5)
Зависимость давления от радиуса р(r) называется депрессионной кривой давления («воронкой» депрессии) и определяется по одной из формул:
(3.6)
(3.7)
Вид распределения давления в пласте при плоскорадиальном течении несжимаемой жидкости и газа представлен на рисунке 7.
Индикаторная линия – зависимость дебита скважины Q от депрессии 
, рис.8. Индикаторная линия строится при установившихся режимах работы скважины и позволяет определить коэффициент продуктивности К, который численно равен дебиту при депрессии, равной единице:
(3.8)
Из формулы Дюпюи (3.5) следует:
(3.9)
Величину 
называют фильтрационным сопротивлением.
Величину 
называют коэффициентом гидропроводности скважины.
Закон движения отмеченных частиц жидкости вдоль линии тока, если при t = 0 частица находилась в точке с координатой r = r0, описывается уравнением:
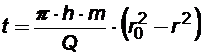(3.10)
Дебит скважины при нарушении закона Дарси вследствие больших скоростей фильтрации определяется в результате интегрирования уравнения Форшгеймера (2.9) при осевой симметрии:
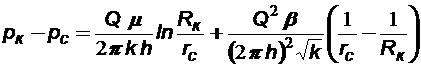(3.11)
Распределение давление круговом пласте в этом случае ьудет определяться формулой:
(3.12)
Если фильтрация происходит по закону Краснопольского (2.11), то дебит определяется по формуле:
(3.13)
3. Фильтрационный поток называется радиально-сферическим, если векторы скорости фильтрации направлены в пространстве по прямым, радиально сходящимся к одной точке (или расходящимся от неё).
|
|
Примером такого потока является приток жидкости к гидродинамической несовершенной скважине малого диаметра, едва вскрывшей непроницаемую горизонтальную кровлю однородного пласта большей мощности, рис.9.
Объёмный дебит такой скважины определяется по формуле:
(3.14)
Приведённое давление в любой точке пласта – по формуле:
(3.15)
Закон движения частиц вдоль линии тока от точки с координатой r0 до точки с координатой r – по формуле:
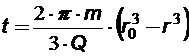(3.16)
Задачи к разделу 3
Задача 3.1
Вывести формулу средневзвешенного по объему порового пространства давления 
:
,
для различных видов течения несжимаемой жидкости и вычислить его при следующих исходных данных: рк =30 МПа, рс(рг)= 10 МПа, Rк(L)= 1 км, rс =0,1 м.
Указание. Интегрирование вести:
1) для плоскопараллельного течения от 0 до L.
2) для плоскорадиального от rс до Rk, пренебречь членами, содержащими rс2, как малые по сравнению с Rk2.
3) для радиально-сферического от rс до Rk, пренебречь членами, содержащими rс3 и rс2.
Задача 3.2
Определить дебит дренажной галереи шириной B = 100 м, если мощность пласта h = 10м, расстояние до контура питания L = 10км, коэффициент проницаемости к = 1 Д, коэффициент динамической вязкости m = 1сПз, давление на контуре питания рк = 9,8 МПа и в галерее рг = 7,35 МПа.
Задача 3.3
Показать графически распределение давления и найти градиент давления при плоскопараллельном движении несжимаемой жидкости в пласте, длина которого L = 5км, мощность пласта h = 10м, ширина галереи B = 300м, коэффициент проницаемости k = 0,8Д, коэффициент динамической вязкости m = 4сПз, давление на галерее рг = 2,94 МПа, дебит галереи Q = 30м3/сут.
|
|
Задача 3.4
Определить величину коэффициента проницаемости (в различных системах единиц) для случая плоскопараллельного установившегося движения однородной жидкости в пласте по закону Дарси по следующим исходным данным: гидравлический уклон 
= 0,03, ширина галереи В = 500 м, мощность пласта h = 6 м, плотность жидкости r =850кг/м3, абсолютная вязкость m = 5сПз и дебит галереи Q = 30м3/сут.
Задача 3.5
Определить массовый дебит нефтяной скважины (в т/сут) в случае установившейся плоскорадиальной фильтрации жидкости по закону Дарси, если известно, что давление на контуре питания рк = 9,8 МПа, давление на забое скважины рс = 7,35 МПа, проницаемость пласта k =500мД, мощность пласта h = 15м, диаметр скважины Dc = 24,8 см, радиус контура питания Rk =10 км, динамический коэффициент вязкости жидкости m = 6сПз и плотность жидкости r = 850кг/м3.
Задача 3.6
Определить давление на расстоянии 10 и 100 м от скважины при плоскорадиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, считая что, мощность пласта h = 10м, коэффициент проницаемости k = 0,5 Д, коэффициент динамической вязкости нефти m = 4сПз, плотность нефти r = 870кг/м3, давление на забое скважины рс = 7,84 МПа, массовый дебит скважины Qm = 200т/сут, радиус скважины rc = 12,4см.
Задача 3.7
Определить коэффициент продуктивности и построить индикаторную линию при плоскорадиальном установившемся движении несжимаемой жидкости по линейному закону фильтрации, если известно что, давление на контуре питания рк = 8,82МПа, радиус контура питания Rк = 10км, мощность пласта h = 10м, коэффициент проницаемости k =600мД, коэффициент динамической вязкости нефти m = 5сПз, диаметр скважины Dc = 24,8 см.
Задача 3.8
Определить значение коэффициента гидропроводности пласта в Д×см/сПз, если известно, что фильтрация происходит по закону Дарси, коэффициент продуктивности К = 18т/(сут (кгс/см2)), радиус контура питания Rk = 1400 м, плотность нефти r = 925 кг/м3, радиус скважины
rc =0,1 м.
Задача 3.9
Определить время отбора нефти из призабойной зоны скважины радиусом r0 = 100м, а также время, за которое частица жидкости пройдет расстояние от контура питания Rk =1,5км до стенки скважины rc =0,1 м, если мощность пласта h = 10м, коэффициент пористости m = 20%, массовый дебит скважины Qm = 40т/сут, плотность нефти r = 920 кг/м3.
Задача 3.10
Как изменится: а) дебит скважины при D р = const, и б) разность давлений между контуром питания и стенкой скважины при Q = const, если увеличить радиус скважины вдвое?
1. Движение происходит по линейному закону фильтрации.
2. Фильтрация происходит по закону Краснопольского.
Начальный радиус скважины rc =0,1 м. Расстояние до контура питания Rk = 5 км.
Задача 3.11
Во сколько раз необходимо увеличить радиус скважины, чтобы дебит ее при прочих равных условиях удвоился?
1) Движение жидкости происходит по закону Дарси.
2) Жидкость фильтруется по закону Краснопольского.
Начальный радиус скважины rc =0,1 м. Расстояние до контура питания Rk = 1 км
Задача 3.12
В центре кругового пласта расположена действующая скважина. Определить пьезометрическую высоту H в простаивающей скважине которая находится на расстоянии r = 200 м, если известно, что дебит действующей скважины Q = 30м3/сут, мощность пласта h = 20м, коэффициент проницаемости k = 700 мД, коэффициент динамической вязкости нефти m = 4сПз, радиус контура питания Rk = 5км, давление на контуре питания рк = 12,75МПа.
Задача 3.13
Определить относительное понижение пьезометрического уровня d:
в реагирующих скважинах, расположенных от возмущающей скважины на расстояниях 1 м, 100 м, 1 км, 10 км. Движение жидкости установившееся плоскорадиальное по закону Дарси. Радиус скважины rc = 10 см, расстояние до контура питания Rк =100 км.
Задача 3.14
Сколько жидкости следует закачивать в пласт в единицу времени через нагнетательную скважину, если необходимо, чтобы давление на стенке скважины поддерживалось в процессе закачки на D р = 1,47МПа выше давления, установившегося в пласте на расстоянии r = 2 км от скважины? Имеет место закон Дарси. мощность пласта h = 10м, коэффициент проницаемости k = 150 мД, коэффициент динамической вязкости нефти m = 1сПз, радиус скважины rс = 10 см.