7.1. Основные положения динамического расчета
кривошипно-шатунного механизма
В процессе работы двигателя внутреннего сгорания (ДВС) в его кривошипно-шатунном механизме (КШМ) действуют силы давления газов, силы инерции возвратно-поступательно движущихся масс и центробежные силы вращающихся масс. Кроме того, при работе ДВС на детали его КШМ воздействуют силы трения, силы тяжести и давление на поршень со стороны картера, которые, вследствие их малых значений, при динамическом расчете двигателя не учитываются.
В течение рабочего цикла действующие в кривошипно-шатунном механизме силы непрерывно изменяют свою величину и направление действия. Для объективной оценки характера изменения этих сил в зависимости от угла поворота коленчатого вала их величины определяют через каждые 10…30º поворота коленчатого вала.
По результатам динамического расчета производят расчеты деталей двигателя на прочность и износ.
Динамический расчет кривошипно-шатунного механизма двигателя внутреннего сгорания начинают с определения сил давления газов и инерционных сил, действующих в КШМ.
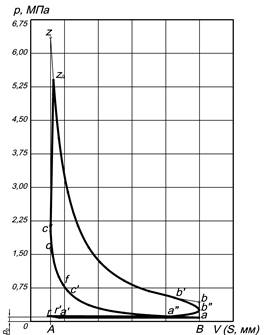
Силы давления газов возникают в результате осуществления в цилиндре рабочего цикла. Эти силы действуют на всю площадь поршня, но для упрощения расчета динамики ДВС их заменяют одной силой P г, приложенной к оси поршневого пальца и направленной по оси цилиндра. Величина этой силы в любой момент времени может быть определена при помощи действительной индикаторной диаграммы, снятой с двигателя, или индикаторной диаграммы, построенной по результатам его теплового расчета. Пример индикаторной диаграммы см. рис. 7.1.
|
| Рис. 7.1. Действительная индикаторная диаграмма двигателя |
|
|
Индикаторная диаграмма двигателя строится в p – V координатах (давление газов – объем надпоршневого пространства). Так как диаметр цилиндра в процессе работы двигателя не изменяется, то величина объема надпоршневого пространства определяется положением поршня в цилиндре, и на диаграмме этот объем выражается через перемещение поршня s. Для получения однозначной зависимости давления газов от времени, выраженного через угол поворота кривошипа φ, производят перестроение (развертку) индикаторной диаграммы из координат p – V в координаты p –φ по методу Ф.А. Брикса (см. рис. 7.2).
По развернутой индикаторной диаграмме определяют значение избыточного давления газов в данный момент времени, МПа
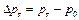 , ,
| (7.1) |
где p г – абсолютное давление газов при данном значении угла поворота кривошипа, МПа; p 0 – атмосферное давление, МПа.
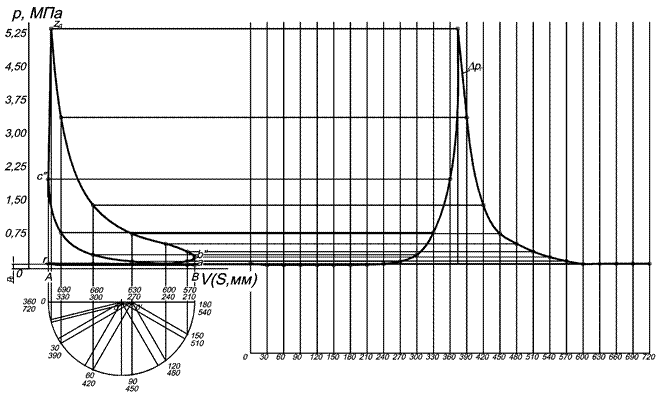
Рис. 7.2. Развертка индикаторной диаграммы в координаты p –φ
По значению значение избыточного давления определяют величину силы давления газов на поршень в этот момент времени.
Реальный кривошипно-шатунный механизм представляет собой систему с распределенными параметрами, элементы которой движутся неравномерно, что вызывает появление инерционных сил. С целью упрощения динамического расчетаосуществляют приведение масс частей кривошипно-шатунного механизма. При этом действительный кривошипно-шатунный механизм заменяют динамически эквивалентной системой сосредоточенных масс.
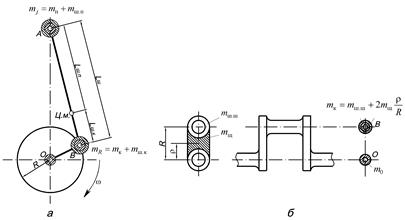
Массу поршневой группы m п, детали которой совершают возвратно-поступательное движение, считают сосредоточенной на оси поршневого пальца в точке A (рис. 7.3, а).
|
|
|
| Рис. 7.3. Система сосредоточения масс, динамически эквивалентная кривошипно-шатунному механизму: а – приведенная система кривошипно-шатунного механизма; б – приведение масс кривошипа |
Элементы шатунной группы совершают сложное плоскопараллельное движение, которое может быть представлено как совокупность возвратно-поступательного движения (верхняя головка шатуна) и вращательного движения (нижняя головка шатуна). Простейшая система масс, эквивалентная по своим инерционным параметрам шатунной группе, состоит из двух масс, одна из которых (m ш.п) сосредоточена на оси поршневого пальца в точке A, а другая (m ш.к) – на оси шатунной шейки в точке B.
Кривошип коленчатого вала совершает равномерное вращательное движение. Его массу заменяют двумя массами, одна из которых (m к) сосредоточена на оси шатунной шейки в точке B, а другая (m 0) – на оси коренной шейки в точке O (рис. 7.3, б). Масса коренной шейки с частью щек, расположенных симметрично относительно оси вращения коленчатого вала, является уравновешенной.
Масса средней части щеки m щ (заштрихованной на рис. 7.3, б) у современных короткоходных двигателей мала по сравнению с массой шатунной шейки m ш.ш, поэтому в большинстве случаев ею пренебрегают и считают, что масса, сосредоточенная в точке B, равна массе шатунной шейки.
Таким образом, система сосредоточенных масс, динамически эквивалентная кривошипно-шатунному механизму, состоит из совершающей возвратно-поступательное движение массы mj, сосредоточенной в точке A, и совершающей вращательное движение массы mR, сосредоточенной в точке B.
|
|
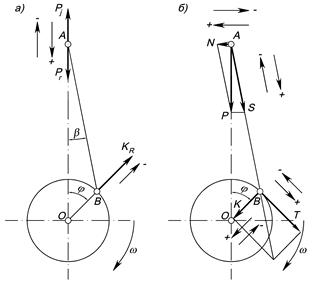
Силы инерции, действующие в кривошипно-шатунном механизме, подразделяют на силы инерции поступательно движущихся масс Pj и центробежные силы вращающихся масс KR (рис. 7.4, а).
|
| Рис. 7.4. Схема действия сил в кривошипно-шатунном механизме: а – инерционных и газовых; б – суммарных |
Силы инерции возвратно-поступательно движущихся масс действуют по оси цилиндра. Силы инерции возвратно-поступательно движущихся масс являются положительными, если они направлены к оси коленчатого вала, и отрицательными, если они направлены от коленчатого вала.
Значения сил инерции возвратно-поступательно движущихся масс определяются по формуле, Н
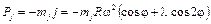 , ,
| (7.2) |
где j – ускорение поршня, м/с2; R – радиус кривошипа, м; ω – угловая скорость коленчатого вала, рад/с; φ – угол поворота кривошипа; λ – параметр, равный отношению радиуса кривошипа к длине шатуна.
Центробежная сила инерции вращающихся масс при постоянной угловой скорости коленчатого вала постоянна по величине, действует по радиусу кривошипа и направлена от оси коленчатого вала. Эта сила является результирующей силы инерции вращающихся масс кривошипа и силы вращающихся масс шатуна.
В двигателях с рядным расположением цилиндров величина центробежной силы инерции вращающихся масс определяется по формуле, Н
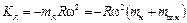 , ,
| (7.3) |
а в V-образных двигателях со сдвоенным кривошипно-шатунным механизмом – по формуле, Н
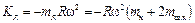 . .
| (7.4) |
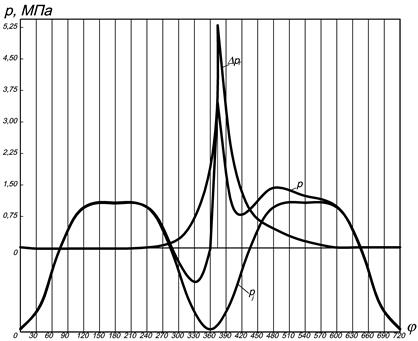
При динамическом анализе кривошипно-шатунного механизма силы давления газов и силы инерции возвратно-поступательно движущихся масс, имеющие общую точку приложения и единую линию действия, заменяют суммарной силой P, являющейся их алгебраической суммой. Графически кривая удельных суммарных сил строится суммированием диаграмм сил давления газов и сил инерции, построенных в одном масштабе (см. рис. 7.5).
|
| Рис. 7.5. Построение кривой удельных суммарных сил |
Воздействие от суммарной силы передается на стенки цилиндра перпендикулярно его оси и на шатун по направлению его оси (рис. 7.4, б). Сила N, действующая перпендикулярно оси цилиндра, называется нормальной силой и воспринимается стенками цилиндра.
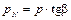 , ,
| (7.5) |
где β – угол отклонения шатуна, град.
Эта сила считается положительной, если создаваемый ею момент относительно оси коленчатого вала направлен противоположно направлению вращения вала. Сила S, действующая вдоль шатуна, воздействует на него, вызывая повторное сжатие-растяжение его элементов, и далее передается кривошипу.
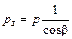 . .
| (7.6) |
Эта сила считается положительной, если сжимает шатун, и отрицательной, если его растягивает.
Действие силы S на сопряжение шатун–кривошип можно оценить, если перенести ее вдоль оси шатуна в точку их шарнирного сочленения (точка B на рис. 7.4, б), где она раскладывается на две составляющие силы: нормальную силу K, направленную по оси кривошипа,
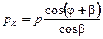 , ,
| (7.7) |
и тангенциальную силу T, направленную по касательной к окружности радиуса кривошипа.
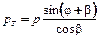 . .
| (7.8) |
Сила K считается положительной, если она сжимает щеки колена. Сила T принимается положительной, если направление создаваемого ею момента совпадает с направлением вращения коленчатого вала.
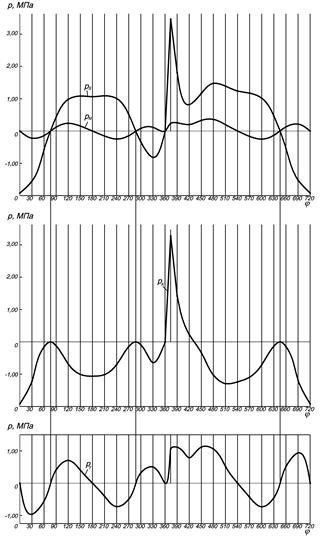
Пример построения графической зависимости сил от угла поворота кривошипа приведен на рис 7.6.
|
| Рис. 7.6. Построение кривых удельных сил pN, pS, pK, pT по углу поворота кривошипа |
Крутящий момент цилиндра определяют как произведение тангенциальной силы T на радиус кривошипа R.
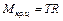 . .
| (7.9) |
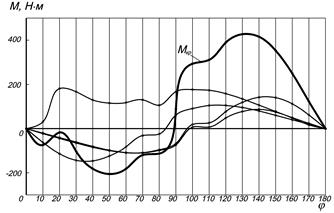
Для построения кривой суммарного крутящего момента M кр многоцилиндрового двигателя производят графическое суммирование кривых крутящих моментов каждого цилиндра, сдвигая одну кривую относительно другой на угол поворота кривошипа между вспышками. Величины и характер изменения крутящих моментов по углу поворота коленчатого вала всех цилиндров двигателя одинаковы и отличаются только угловыми интервалами, равными угловым интервалам между вспышками в отдельных цилиндрах. Поэтому для подсчета суммарного крутящего момента двигателя достаточно иметь кривую крутящего момента одного цилиндра. Пример построения кривой суммарного крутящего момента двигателя показан на рис. 7.7.
|
| Рис. 7.7. Построение кривой суммарного крутящего момента двигателя |