Лекция 9 Криволинейный полет ЛА в вертикальной плоскости
Нагрузки, действующие на ЛА при криволинейном полете в вертикальной плоскости, показаны на рис. 1. Назовем принятые на нем обозначения (помимо упомянутых раньше): 0 –центр тяжести;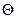 
- угол тангажа; θ - угол наклона траектории.
В центре тяжести ЛА приложены: проекции аэродинамических сил Y, Х, сила веса G и инерционные силы в виде тангенциальной 
и радиальной составляющих 
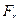. По оси корпуса действует сила тяги Т. При переносе аэродинамических и инерционных сил в центр тяжести возникает аэродинамический 
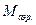и инерционный 
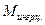моменты. Аэродинамические силы и силы тяги называются поверхностными силами, а силы веса и инерционные - массовыми.
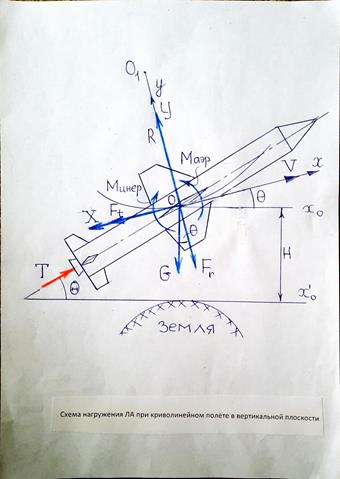Рис.1
Между поверхностными и массовыми силами существует связь, которую можно получить, если составить уравнения динамического равновесие сил, пользуясь принципом Даламбера:
В случае несвободной материальной точки активные силы, приложенные к ней, уравновешиваются силами инерции.
На основании принципа Даламбера уравнения движения материальной точки можно формально получить из уравнений равновесия, приложив при этом к действующим на точку силам силы инерции. В случае несвободной материальной точки силой инерции называется главный вектор сил противодействия, частично предложенных к телам, действия которых на рассматриваемую точку вызывают ее ускорение, и частично - к связям.
Рассмотрим условия равновесия ЛА под действием всех названных сил и моментов:
Проекция всех сил на ось X:
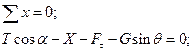
Проведем очевидные преобразования, тогда получим:
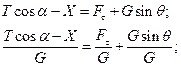(1)
где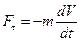 
- инерционная сила, действующая по вектору скорости ЛА.
Обратим внимание, что в левой части выражения (1) стоит член, означающий перегрузку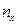 
, что было установлено раньше. Принимая это во внимание, находим:
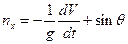(2)
Проекция всех сил на ось Y:
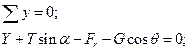
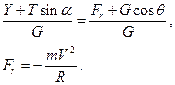
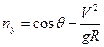(3)
Отсюда следует важное заключение: перегрузку можно выразить не только через поверхностные силы (1), но и через параметры траектории (2), (3), что дает возможность, зная эти параметры (V,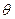 
, g, следовательно, высоту полета), управлять перегрузкой и ЛА в полете.
Далее, обратимся к моментам.
Сумма моментов относительно центра масс (тяжести):
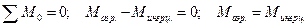
Аэродинамический момент 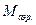равен сумме моментов от всех поверхностных сил относительно центра масс ЛА.
Инерционный момент 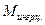определяется по формуле:
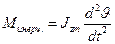
Инерционные силы определяются через радиус кривизны траектории R, скорость полёта V, массу m, массовый момент инерции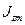 
, угол тангажа 
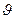ЛА.
Примечание: на схеме движения ЛА (Рис.1) инерционная сила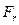 
направлена в соответствии с ускоренным движением ЛА (
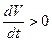), а в формуле перед членом 
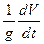стоит знак минус в соответствии с принятым замедленным движением, при этом производная берется по абсолютному значению.
При расчетах ЛА на прочность, как правило, применяются перерезывающие силы и соответствующие перегрузки, поэтому полезно установить связь этих сил с подъемной силой и перегрузок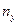 
с поперечной перегрузкой 
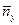. Установим связь между силами в скоростных и связанных осях, так как для расчета на прочность необходимо иметь составляющие сил в связанных осях, ибо они дают непосредственно поперечные и осевые нагрузки на ЛА. Между этими силами существует связь:
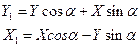
Поперечная и осевая перегрузки выражаются через поперечную и осевую силы по формулам:
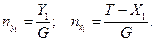
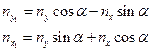
Если траектория полета ЛА известна, то по формулам можно найти перегрузки
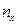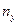, , а по их значениям - действующие в тот или иной момент времени силы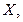 
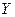. Далее, можно определить нагрузки 
, 
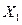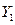, однако, такой путь не всегда осуществим, так как для манёвренных ЛА (ЗУРы, самолёты и др.) невозможно заранее установить траектории их полета, потому что в окончательном виде они определяются только в процессе самого полёта.