Основные определения.
Пару  действительных чисел а и b называют упорядоченной, если указано, какое из них считается первым, какое – вторым.
действительных чисел а и b называют упорядоченной, если указано, какое из них считается первым, какое – вторым.
Определение 1. Комплексным числом называется любая упорядоченная пара
 действительных чисел R.
действительных чисел R.
Множество всех комплексных чисел обозначается С.
Определение 2. Два комплексных числа  и
и  считают равными и
считают равными и
пишут  =
=  , если
, если 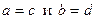 .
.
Условимся в дальнейшем комплексные числа обозначать строчными буквами греческого алфавита.
Определение 3. Пусть  и
и  - два комплексных числа.
- два комплексных числа.
Сумма  определяется равенством
определяется равенством
 ,
,
а произведение  - равенством
- равенством
 .
.
Операции сложения и умножения комплексных чисел обладают следующими свойствами:
1.  (коммутативность сложения.)
(коммутативность сложения.)
2. 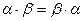 (коммутативность умножения).
(коммутативность умножения).
3.  (ассоциативность сложения).
(ассоциативность сложения).
4.  (ассоциативность умножения).
(ассоциативность умножения).
5.  (дистрибутивность умножения относительно сложения).
(дистрибутивность умножения относительно сложения).
Упражнение. Проверить свойства 1-5.
Упорядоченная пара  обладает тем свойством, что сложение ее с любой другой упорядоченной парой не меняет этой пары:
обладает тем свойством, что сложение ее с любой другой упорядоченной парой не меняет этой пары:  . Упорядоченная пара
. Упорядоченная пара  играет роль нуля при сложении упорядоченных пар; называют ее нуль-парой.
играет роль нуля при сложении упорядоченных пар; называют ее нуль-парой.
Определение 4. Пусть  и
и  - два комплексных числа.
- два комплексных числа.
Разностью  двух упорядоченных пар называют такую
двух упорядоченных пар называют такую
упорядоченную пару  , что
, что  .
.
Найдем x и y. Поскольку 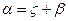 , то
, то  , т.е.
, т.е.  ,
,  , откуда
, откуда  ,
,  .
.
Таким образом, вычитание упорядоченных пар определяется формулой
 .
.
Определение 5. Частным  двух упорядоченных пар
двух упорядоченных пар  и
и
 называют такую упорядоченную пару
называют такую упорядоченную пару  , что
, что
 .
.
Найдем x и y. Так как  , то
, то  , т.е.
, т.е.  ,
,  . Эта система имеет решение
. Эта система имеет решение  ,
,  .Если
.Если  , т.е.
, т.е. 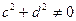 , то частное
, то частное  двух упорядоченных пар определяется так:
двух упорядоченных пар определяется так:  .
.
Из последнего равенства при  , т.е.
, т.е. 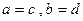 , получаем, что
, получаем, что
 .
.
Значит, роль единицы при делении упорядоченных пар выполняет упорядоченная пара 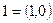 .
.
1.1.2 Множество комплексных чисел как расширение множества действительных чисел.
Рассмотрим комплексные числа вида 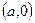 . Множество, состоящее из всех таких чисел, обозначим С*.
. Множество, состоящее из всех таких чисел, обозначим С*.
Если каждому действительному числу а сопоставим комплексное число 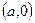 , т. е.
, т. е.  , то получим некоторое соответствие между множеством R и множеством С*. Это соответствие является взаимно однозначным.
, то получим некоторое соответствие между множеством R и множеством С*. Это соответствие является взаимно однозначным.
Для любых двух действительных чисел а и b имеем  . Если учесть, что
. Если учесть, что  , то можно записать
, то можно записать  . Это означает, что сумме действительных чисел а и b отвечает сумма соответствующих им комплексных чисел.
. Это означает, что сумме действительных чисел а и b отвечает сумма соответствующих им комплексных чисел.
То же самое относится к произведению: так как  и
и  , то
, то  . Итак, произведению действительных чисел а и b отвечает произведение соответствующих им комплексных чисел.
. Итак, произведению действительных чисел а и b отвечает произведение соответствующих им комплексных чисел.
Из сказанного следует, что если отождествить каждое действительное число а с комплексным числом 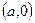 , то тем самым множество R действительных чисел с его обычной арифметикой окажется как бы вложенным в множество С комплексных чисел. В этом смысле говорят, что множество комплексных чисел является расширением множества действительных чисел.
, то тем самым множество R действительных чисел с его обычной арифметикой окажется как бы вложенным в множество С комплексных чисел. В этом смысле говорят, что множество комплексных чисел является расширением множества действительных чисел.
1.1.3 Алгебраическая форма комплексного числа.
Арифметические действия над комплексными числами.
Сопряженные комплексные числа. Свойства операции сопряжения.
Условимся в дальнейшем не делать различия между комплексным числом вида  и действительным числом а, т. е.
и действительным числом а, т. е.  ; основанием для такого соглашения являются одинаковые «арифметики» в множествах R и С*.
; основанием для такого соглашения являются одинаковые «арифметики» в множествах R и С*.
Рассмотрим упорядоченную пару 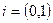 . Согласно закону умножения комплексных чисел, имеем
. Согласно закону умножения комплексных чисел, имеем  , тогда
, тогда  .
.
Определение 6. Упорядоченную пару 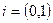 ,.удовлетворяющую
,.удовлетворяющую
соотношению  или
или  , называют мнимой единицей.
, называют мнимой единицей.
С помощью мнимой единицы можно выразить любое комплексное число. В самом деле, так как
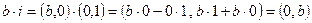 ,
,
то
 .
.
Теперь можно забыть о первоначальном способе задания комплексного числа как пары  и записывать комплексное число в виде
и записывать комплексное число в виде  .
.
Определение 7. Выражение  называют алгебраической формой
называют алгебраической формой
комплексного числа. Число а называют действительной частью,
число b – мнимой частью комплексного числа  .
.
Если задано комплексное число  , то действительную часть числа
, то действительную часть числа  обозначают
обозначают  (от франц. reele – «действительный»), а мнимую -
(от франц. reele – «действительный»), а мнимую -  (от франц. imaginaire – «мнимый»). Например,
(от франц. imaginaire – «мнимый»). Например,  ,
, 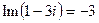 .
.
Если  , то число
, то число  - действительное; если
- действительное; если 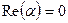 , то число
, то число  имеет вид
имеет вид  и называется чисто мнимым.
и называется чисто мнимым.
Определение 8. Пусть 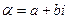 . Число
. Число 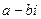 , отличающееся от
, отличающееся от  лишь
лишь
знаком коэффициента при мнимой части, называется
сопряженным числу  и обозначается
и обозначается  .
.
Итак, по определению, 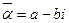 .
.
Если  - действительное число, т.е.
- действительное число, т.е. 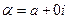 , то
, то  . Таким образом, любое действительное число равно своему сопряженному.
. Таким образом, любое действительное число равно своему сопряженному.
Из определения комплексного числа (как упорядоченной пары действительных чисел) и определения арифметических действий над упорядоченными парами следует, что
1. 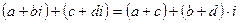 ,
,
2.  ,
,
3.  ,
,
4.  .
.
Формула 1 определяет правило сложения двух комплексных чисел: чтобы сложить два комплексных числа, необходимо сложить отдельно их действительные и мнимые части. Формула 2 означает, что при вычитании одного комплексного числа из другого, необходимо вычесть отдельно их действительные и мнимые части.
Формулу 3 можно получить путем умножения по правилам алгебры и замены 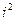 его значением:
его значением:
 .
.
Чтобы получить формулу 4, необходимо предварительно числитель и знаменатель умножить на  (число сопряженное числу
(число сопряженное числу  ):
):  .
.
Сформулируем основные свойства операции сопряжения:
1)  ; 4)
; 4) 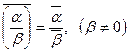 ;
;
2)  ; 5)
; 5) 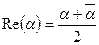 ;
;
3)  ; 6)
; 6)  .
.
Упражнение 2. Доказать свойства 1-5 операции сопряжения.