ИДЗ-6
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
ЗАДАНИЯ
(номер варианта соответствует номеру в списке)
Задание 1. Решить задачи
1. Составить уравнение плоскости, проходящей через ось Ох перпендикулярно к плоскости  .
2. Написать канонические уравнения прямой: .
2. Написать канонические уравнения прямой:  .
3. Проверить, лежит ли прямая .
3. Проверить, лежит ли прямая  на плоскости на плоскости  . .
| |
| 2. | 1. Плоскость a проходит через точки А (-1; 3; 4), B (-1; 5; 0) и C (2; 6; 1), плоскость b задана уравнением 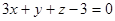 . Показать, что плоскости перпендикулярны, и выяснить, какая из них расположена ближе к началу координат.
2. Через точку М (2; 3; -1) провести плоскость, параллельную плоскости . Показать, что плоскости перпендикулярны, и выяснить, какая из них расположена ближе к началу координат.
2. Через точку М (2; 3; -1) провести плоскость, параллельную плоскости 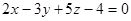 . Составить для построенной плоскости уравнение в "отрезках".
3. Показать, что прямые . Составить для построенной плоскости уравнение в "отрезках".
3. Показать, что прямые 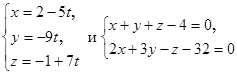 взаимно перпендикулярны. взаимно перпендикулярны.
|
| 3. | 1. Написать уравнение плоскости, проходящей через точку М (-3; 1; 2) параллельно векторам 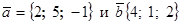 . Найти угол между построенной плоскостью и плоскостью . Найти угол между построенной плоскостью и плоскостью  .
2. Найти острый угол между прямыми, одна из которых задана уравнением .
2. Найти острый угол между прямыми, одна из которых задана уравнением  , другая проходит через точки А (2; -5; 3) и В (13; 2; -5).
3. При каких значениях В и n прямая , другая проходит через точки А (2; -5; 3) и В (13; 2; -5).
3. При каких значениях В и n прямая 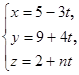 перпендикулярна плоскости перпендикулярна плоскости 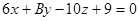 ? ?
|
| 4. | 1. При каком значении l плоскости a и b будут перпендикулярны? Плоскость a проходит через точки К (-1; 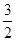 ; 0), М (2; -1; 1), N (8; 1; -1). Плоскость b задана уравнением ; 0), М (2; -1; 1), N (8; 1; -1). Плоскость b задана уравнением 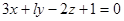 .
2. Найти угол между прямыми .
2. Найти угол между прямыми  и и  .
3. Найти значение m, при котором прямая .
3. Найти значение m, при котором прямая  параллельна плоскости параллельна плоскости 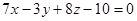 . .
|
| 5. | 1. Найти угол между плоскостями a и b, где a проходит через точки A (1;  ; ;  ), В (2; 0; 1) параллельно оси OZ, а b - через точки С (2; 2; 1), D (6; 1; 0) и E (-1; -1; 3).
2. Написать канонические уравнения прямой: ), В (2; 0; 1) параллельно оси OZ, а b - через точки С (2; 2; 1), D (6; 1; 0) и E (-1; -1; 3).
2. Написать канонические уравнения прямой:  .
3. Найти угол между прямой .
3. Найти угол между прямой  и плоскостью и плоскостью 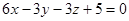 . .
|
| 6. | 1. Написать канонические уравнения прямой: 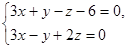 .
2. Найти точку пересечения прямой .
2. Найти точку пересечения прямой 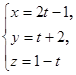 с плоскостью с плоскостью  и угол между ними.
3. Написать уравнение плоскости, проходящей через точку М (-3; 5; -1) и перпендикулярно прямой и угол между ними.
3. Написать уравнение плоскости, проходящей через точку М (-3; 5; -1) и перпендикулярно прямой  . .
|
| 7. | 1. Найти угол между плоскостью 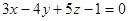 и плоскостью, проходящей через точки М (1; 1; 1) и N (2; 3; -1) параллельно вектору и плоскостью, проходящей через точки М (1; 1; 1) и N (2; 3; -1) параллельно вектору 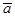 ={0; -1; 2}.
2. Написать канонические уравнения прямой: ={0; -1; 2}.
2. Написать канонические уравнения прямой:  .
3. При каком значении n прямые .
3. При каком значении n прямые 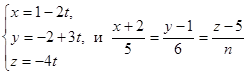 будут взаимно перпендикулярны? будут взаимно перпендикулярны?
|
| 8. | 1. Составить уравнения прямой, проходящей через точки пересечения плоскости 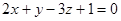 с прямыми с прямыми 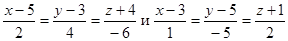 .
2. При каком значении m прямые .
2. При каком значении m прямые  будут взаимно перпендикулярны?
3. Написать уравнение плоскости, которая проходит через точку М (3; 1; -2) и прямую будут взаимно перпендикулярны?
3. Написать уравнение плоскости, которая проходит через точку М (3; 1; -2) и прямую  . .
|
| 9. | 1. Плоскость a проходит через точку М (-5; 4; 13) и отсекает на осях координат равные отрезки. Плоскость b задана уравнением,  . При каком значении m плоскости a и b будут перпендикулярны?
2. Написать канонические уравнения прямой: . При каком значении m плоскости a и b будут перпендикулярны?
2. Написать канонические уравнения прямой: 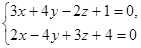 3. При каких значениях А и С прямая
3. При каких значениях А и С прямая  лежит в плоскости лежит в плоскости 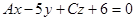 ? ?
|
| 10. | 1. Найти уравнение плоскости, проходящей через точки М (1; -1; 2), N (3; 1; -2) и перпендикулярной к плоскости ХОY.
2. Написать канонические уравнения прямой: 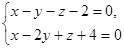 .
3. При каком значении С плоскость .
3. При каком значении С плоскость  будет параллельна прямой будет параллельна прямой  . .
|
| 11. | 1. Написать уравнение плоскости, проходящей через точку М(1; 1; 1) параллельно векторам 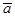 ={0; 1; 2} и ={0; 1; 2} и  = {-1; 0; l}.Указать особенность в расположении плоскости.
2. Найти проекцию точки М (1; 2; -3) на плоскость = {-1; 0; l}.Указать особенность в расположении плоскости.
2. Найти проекцию точки М (1; 2; -3) на плоскость  .
3. Параллельны ли прямые .
3. Параллельны ли прямые 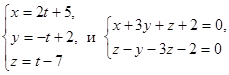 ? ?
|
| 12. | 1. Написать уравнение плоскости, проходящей через точки М(1; 2; 0) и N(2; 1; 1) параллельно вектору 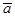 ={3; 0; 1}. Полученное уравнение привести к уравнению в отрезках.
2. Написать канонические уравнения прямой: ={3; 0; 1}. Полученное уравнение привести к уравнению в отрезках.
2. Написать канонические уравнения прямой: 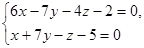 .
3. При каких значениях В и D прямая .
3. При каких значениях В и D прямая 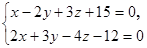 лежит в плоскости лежит в плоскости 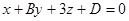 ? ?
|
| 13. | 1. Найти расстояние от точки М (0; -1; 1) до плоскости, проходящей через точки А(1; 4; -5) и В(4; 2; -3) и перпендикулярной плоскости  .
2. Найти точку пересечения прямой .
2. Найти точку пересечения прямой 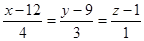 с плоскостью с плоскостью 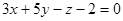 и угол между ними.
3. При каком значении m прямые и угол между ними.
3. При каком значении m прямые 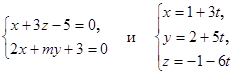 будут взаимно перпендикулярны? будут взаимно перпендикулярны?
|
| 14. | 1. Определить объем тетраэдра, ограниченного координатными плоскостями и плоскостью, проходящей через точку М(-3; -6; 4) перпендикулярно вектору 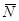 ={2; -1; 6}.
2. Найти острый угол между прямыми: ={2; -1; 6}.
2. Найти острый угол между прямыми:  3. Прямая проходит через точки А(3; -1; 0) и В(х; -7; 3) и параллельна плоскости
3. Прямая проходит через точки А(3; -1; 0) и В(х; -7; 3) и параллельна плоскости  . Определить абсциссу точки В. . Определить абсциссу точки В.
|
1. Найти расстояние от точки М(2; 1; 1) до плоскости, проходящей через точку N(-1; -1; 2) и перпендикулярной плоскостям  .
2. Плоскость проходит через точки А(3; 1; 1), В(-7; .
2. Плоскость проходит через точки А(3; 1; 1), В(-7;  ; 0) и С(-1; 1; ; 0) и С(-1; 1;  ). Написать уравнение прямой, проходящей через точку А перпендикулярно к этой плоскости.
3. При каких значениях m и n прямые ). Написать уравнение прямой, проходящей через точку А перпендикулярно к этой плоскости.
3. При каких значениях m и n прямые 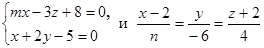 будут параллельны? будут параллельны?
| |
| 16. | 1. Найти угол между плоскостями a и b, где a проходит через точку А (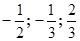 ) перпендикулярно оси OZ, a b - через точки В(2; -1; -1), С(-1; 0; 2) и D(0; -2; 0).
2. При каком значении n прямые ) перпендикулярно оси OZ, a b - через точки В(2; -1; -1), С(-1; 0; 2) и D(0; -2; 0).
2. При каком значении n прямые 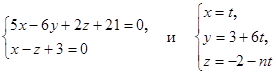 будут взаимно перпендикулярны?
3. Составить уравнения прямой, проходящей через точку М(3; -1; -4), перпендикулярно плоскости будут взаимно перпендикулярны?
3. Составить уравнения прямой, проходящей через точку М(3; -1; -4), перпендикулярно плоскости  . Найти точку пересечения прямой и плоскости. . Найти точку пересечения прямой и плоскости.
|
| 17. | 1. Из точки Р(-1; 1; 4) опущен на плоскость перпендикуляр, основанием которого является точка Q(2; 1; 3). Составить уравнение плоскости и указать особенности в её расположении.
2. Написать канонические уравнения прямой:  .
3. При каком значении р прямые .
3. При каком значении р прямые  будут параллельны? будут параллельны?
|
| 18. | 1. Определить, при каких значениях m и n плоскости 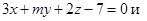  будут параллельны, и найти расстояние между ними.
2. Найти угол между прямыми, одна из которых задана уравнением будут параллельны, и найти расстояние между ними.
2. Найти угол между прямыми, одна из которых задана уравнением 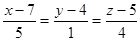 , другая проходит через точку А(1; 2; 3) и точку пересечения указанной прямой с плоскостью , другая проходит через точку А(1; 2; 3) и точку пересечения указанной прямой с плоскостью  .
3. Составить уравнение плоскости, проходящей через точку М(-3; 1; 0) и через прямую .
3. Составить уравнение плоскости, проходящей через точку М(-3; 1; 0) и через прямую  . .
|
| 19. | 1. Составить уравнение плоскости, проходящей через точки А(4; 6; -3), B(-2; -1; 7) и отсекающей равные отрезки на осях ОУ и OZ. Найти расстояние от точки С(5; -7; 8) до построенной плоскости.
2. Провести через точку пересечения плоскости  с прямой с прямой 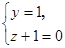 прямую, лежащую в этой плоскости и перпендикулярную к данной прямой.
3. Прямая проходит через точки А(х; 5; 9), В(2; у; 21) и параллельна прямой прямую, лежащую в этой плоскости и перпендикулярную к данной прямой.
3. Прямая проходит через точки А(х; 5; 9), В(2; у; 21) и параллельна прямой 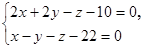 . Определить абсциссу точки А, ординату точки В. . Определить абсциссу точки А, ординату точки В.
|
| 20. | 1. Найти угол между плоскостями a и b, где a. проходит через точку М(3; -1; -2) параллельно плоскости XOZ, a b отсекает на осях координат отрезки a = 2, b = -4,  .
2. Написать канонические уравнения прямой: .
2. Написать канонические уравнения прямой:  .
3. Написать уравнение прямой, проходящей через точку М(3; 5; 1) параллельно прямой .
3. Написать уравнение прямой, проходящей через точку М(3; 5; 1) параллельно прямой 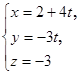 . .
|
| 21. | 1. Найти угол между плоскостями a и b, где a проходит через точки А( ) и B( ) и B(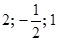 ) параллельно оси OY, а b задана уравнением ) параллельно оси OY, а b задана уравнением  .
2. Написать канонические уравнения прямой: .
2. Написать канонические уравнения прямой: 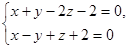 .
3. Составить уравнение плоскости, проходящей через прямую .
3. Составить уравнение плоскости, проходящей через прямую  параллельно прямой параллельно прямой 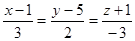 . .
|
| 22. | 1. Через точку А(-2; 4; 8) проведены две плоскости: одна из них содержит ось OX, другая - OZ. Вычислить угол между этими плоскостями.
2. Плоскость a проходит через точки А(х; 1; 2), В(-2; 1; 1), С(2; -1; -2); плоскость b задана уравнением  . Определить абсциссу точки А так, чтобы плоскости были перпендикулярными.
3. Написать канонические уравнения прямой: . Определить абсциссу точки А так, чтобы плоскости были перпендикулярными.
3. Написать канонические уравнения прямой:  . .
|
| 23. | 1. На осях координат отложены от начала координат отрезки, соответственно равные 1, 2 и 3 ед.; концы этих отрезков соединены прямыми. Найти точку пересечения и угол между плоскостью полученного треугольника и прямой, проходящей через точки А(0; 4; -2), В (3; -1; 2).
2. Составить уравнения прямой, проходящей через точку М(-4; 3; -8) перпендикулярно двум прямым:  .
3. При каком значении n прямая .
3. При каком значении n прямая 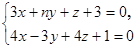 параллельна плоскости параллельна плоскости  ? ?
|
| 24. | 1. Найти расстояние от точки К (3; -2; 1) до плоскости, проходящей через точки М (5; -4; 3) и N (-2; 1; 8) и перпендикулярной плоскости YOZ.
2. Написать канонические уравнения прямой: 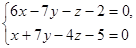 .
3. Доказать, что прямые .
3. Доказать, что прямые 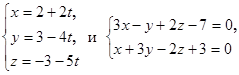 параллельны. параллельны.
|
| 25. | 1. Составить уравнение плоскости, проходящей через точки А(10; -5; 2), B(16; 3; 11), С(-11; -33; 0), и указать особенность в её расположении.
2. Написать канонические уравнения прямой:  .
3. Найти угол между прямыми, одна из которых задана уравнением .
3. Найти угол между прямыми, одна из которых задана уравнением 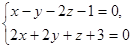 другая проходит через точки М(1; 0; 3) и N(5; -2; 7). другая проходит через точки М(1; 0; 3) и N(5; -2; 7).
|
| 26. | 1. Плоскость α проходит через точку M1(1; 3; 1) параллельно плоскости  . Плоскость β проходит через точку M2(5; -1; 2) и содержит ось . Плоскость β проходит через точку M2(5; -1; 2) и содержит ось  . Найти угол между плоскостями α и β.
2. Написать каноническое уравнения прямой . Найти угол между плоскостями α и β.
2. Написать каноническое уравнения прямой  .
3. Через точку M1(2; 3; 6) провести плоскость перпендикулярную прямой .
3. Через точку M1(2; 3; 6) провести плоскость перпендикулярную прямой 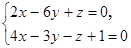 . .
|
| 27. | 1. Составить уравнение плоскости, проходящей через точки M1(1; 1; 1), M2(2; 3; 4) и перпендикулярной плоскости 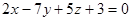 . Полученное уравнение привести к уравнению в отрезках и построить плоскость. Найти объем пирамиды, образованной этой плоскостью и координатными плоскостями.
2. Составить уравнение прямой, проходящей через точку B(3; 4; -4) параллельно прямой . Полученное уравнение привести к уравнению в отрезках и построить плоскость. Найти объем пирамиды, образованной этой плоскостью и координатными плоскостями.
2. Составить уравнение прямой, проходящей через точку B(3; 4; -4) параллельно прямой  . При каком m построенная прямая будет перпендикулярна прямой . При каком m построенная прямая будет перпендикулярна прямой  .
3. При каких значениях A и B прямая .
3. При каких значениях A и B прямая 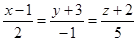 лежит в плоскости лежит в плоскости  . .
|
1. Плоскость α проходит через точку Р(2; 1; 1) и отсекает на осях ох и oy отрезки, соответственно равные 4 и -6. Плоскость β задана уравнением  . При каких m и n плоскости будут параллельны? Найти расстояние между этими плоскостями.
2. При каком n плоскость . При каких m и n плоскости будут параллельны? Найти расстояние между этими плоскостями.
2. При каком n плоскость 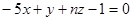 будет параллельна прямой будет параллельна прямой  ?
3. Прямая α проходит через точки M1(3; 4; 7) и M2(-1; 3; 3). Прямая β проходит через точку Р(3; 2; -1) параллельно прямой ?
3. Прямая α проходит через точки M1(3; 4; 7) и M2(-1; 3; 3). Прямая β проходит через точку Р(3; 2; -1) параллельно прямой  . Найти угол между прямыми α и β. . Найти угол между прямыми α и β.
| |
1. Составить уравнение плоскости, проходящей через ось Ох перпендикулярно к плоскости 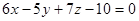 .
2. Написать канонические уравнения прямой: .
2. Написать канонические уравнения прямой:  .
3. Проверить, лежит ли прямая .
3. Проверить, лежит ли прямая  на плоскости на плоскости 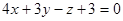 . .
| |
1. Плоскость a проходит через точки А (-1; 3; 4), B (-1; 5; 0) и C (2; 6; 1), плоскость b задана уравнением 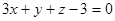 . Показать, что плоскости перпендикулярны, и выяснить, какая из них расположена ближе к началу координат.
2. Через точку М (2; 3; -1) провести плоскость, параллельную плоскости . Показать, что плоскости перпендикулярны, и выяснить, какая из них расположена ближе к началу координат.
2. Через точку М (2; 3; -1) провести плоскость, параллельную плоскости  . Составить для построенной плоскости уравнение в "отрезках".
3. Показать, что прямые . Составить для построенной плоскости уравнение в "отрезках".
3. Показать, что прямые 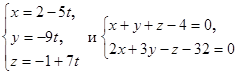 взаимно перпендикулярны. взаимно перпендикулярны.
|
Задание 2. Изучить основные виды поверхностей второго порядка. Результаты оформить в виде таблицы 1.
Рекомендуемая литература. Письменный, Д. Т. Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. - М.: Айрис-пресс, 2011.С. 104 -115.
Таблица 1
Основные виды поверхностей второго порядка
| Название поверхности | Каноническое уравнение | Чертеж |
| Сфера | ||
| Эллипсоид | ||
| Однополостной гиперболоид | ||
| Двуполостной гиперболоид | ||
| Эллиптический параболоид | ||
| Гиперболический параболоид | ||
| Конус второго порядка | ||
| Цилиндры второго порядка - эллиптический цилиндр - гиперболический цилиндр - параболический цилиндр |
Задание 3. Определить вид поверхностей второго порядка, сделать схематический чертеж.
| 1. | а) 
| б) 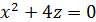
|
| 2. | а) 
| б) 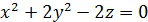
|
| 3. | а) 
| б) 
|
| 4. | а) 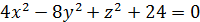
| б) 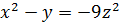
|
| 5. | а) 
| б) 
|
| 6. | а) 
| б) 
|
| 7. | а) 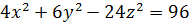
| б) 
|
| 8. | а) 
| б) 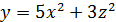
|
| 9. | а) 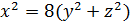
| б) 
|
| 10. | а) 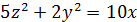
| б) 
|
| 11. | а) 
| б) 
|
| 12. | а) 
| б) 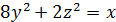
|
| 13. | а) 
| б) 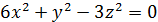
|
| 14. | а) 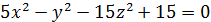
| б) 
|
| 15. | а) 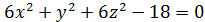
| б) 
|
| 16. | а) 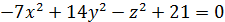
| б) 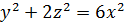
|
| 17. | а) 
| б) 
|
| 18. | а) 
| б) 
|
| 19. | а) 
| б) 
|
| 20. | а) 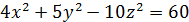
| б) 
|
| 21. | а) 
| б) 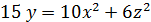
|
| 22. | а) 
| б) 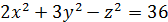
|
| 23. | а) 
| б) 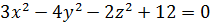
|
| 24. | а) 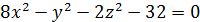
| б) 
|
| 25. | а) 
| б) 
|
| 26. | а) 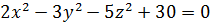
| б) 
|
| 27. | а) 
| б) 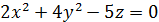
|
| 28. | а) 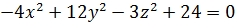
| б) 
|
а) 
| б) 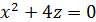
| |
а) 
| б) 
|