1.
-Прочность конструкции заключается в свойстве конструкции сопротивляться разрушению в целом или отдельных ее элементов.
-Жесткость конструкции характеризуется способностью сопротивляться возникновению в ней перемещений.
-Устойчивость состоит в способности конструкции сохранять заданное положение в пространстве и исходную форму равновесия в деформированном состоянии.
-Строительная механика в широком смысле слова включает в себя следующие дисциплины: сопромат, теорию упругости/пластичности/ползучести, строймех стержневых систем, строймех тонкостенных пространственных систем.
- Строительная механика в узком смысле слова включает в себя разработку методов определения внутренних усилий и перемещений (строймех стержневых систем).
- Основная задача строительной механики стержневых систем является разработка методов расчета и получения данных для надежного и экономичного проектирования зданий и сооружений.
- Направление схематизации конструкции при образовании ее расчетной модели:
1.моделирование геометрических конструкций
2.моделирование материальных конструкций
3.моделирование воздействий на конструкцию
4.моделирование прочности конструкции
- Составляющие схематизации геометрии конструкции (схематизация изображений геометрической формы конструкции за счет упрощений в изображениях элементов конструкций, узловых соединений и опорных закрепителей) :
1.схематизация изображений элементов конструкции
2.схематизация изображений узловых соединений элементов конструкции между собой
3.схематизация изображения опорных устройств конструкции
- Расчетная схема конструкции называется упрощенное изображение, применяемое при расчете конструкций, которое отражает наиболее существенные особенности геометрической формы, определяющие восприятие конструкций внешних воздействий.
- Виды внешних воздействий на конструкции:
1.силовое воздействие(нагрузка)
2.температурное воздействие(температура)
3.кинематическое воздействие(осадка опор)
4.другие(электромагнитные, биохимические и прочее)
- Несущая способность конструкции – это свойство конструкции воспринимать нагрузки и оставаться прочной, то есть не получать разрушения в целом или отдельных её элементов.
- Методы определения несущей способности конструкции:
1.расчет по допускаемым напряжениям
2.расчет по разрушающим нагрузкам
3.расчет по предельным состояниям
-Параметры напряженно-деформируемого состояния (НДС) конструкции:
-Кривая равновесных состояний – это линия, которая в системе осей НДС описывает всё множество состояний равновесия конструкции при её статической нагрузки от О до несущей конструкции (рис).
Р – 
нагрузка
Δ – перемещение
Р0 – ненагруженно
Δ0 – исходное положение
Рпр – предельно
Δпр – состояние равновесия
- Линейно деформируемая система – это расчетная модель конструкции, у которой между нагрузкой вызываемыми ею перемещениями, а также внутренними усилиями принимается прямая пропорциональная зависимость (рис).
- Принцип независимости действия сил заключается в том, что при действии на конструкцию нескольких нагрузок возникающие внутренние усилия и перемещения равняются сумме внутренних усилий и перемещений от действия каждой нагрузки в отдельности.
- Принцип начальных размеров заключается в том, что при составлении уравнений равновесия конструкции не учитываются изменения её формы и размеров вследствие деформирования.
- Нелинейно деформируемой системой называется расчетная модель конструкции, у которой между нагрузкой и вызываемыми ею перемещениями принимается нелинейная зависимость (рис).
- Виды нелинейно деформируемых систем:
1.геометрически нелинейные системы
2.физически нелинейные системы
3.геометрически и физически нелинейные системы
- Виды расчетных схем конструкций по статическому признаку
1.статически определимые
2.статически неопределимые
3.статически противоречивые
- Виды расчетных схем конструкций по кинематическому признаку
1.геометрически неизменяемые
2.геометрически изменяемые
- Взаимосвязь статических и кинематических признаков расчетных схем конструкций:
1.геометрически изменяемые системы с любым типом изменяемости являются статически противоречивыми системами
2.геометрически неизменяемые системы с необходимым числом связей являются статически определимыми системами
3.геометрически неизменяемые системы с избыточным числом элементов являются статически неопределимыми системами
-Расчетная схема конструкции считается геометрически неизменяемой системой, если она не допускает относительные перемещения элементов без деформации материала.
- Виды геометрически неизменяемых систем:
1.с необходимым числом связей
2.с избыточным числом связей
-Расчетная схема конструкции считается геометрически изменяемой системой, если она допускает относительные перемещения элементов без деформации материала.
- Виды геометрически изменяемых систем:
1.с конечной изменяемостью
2.с мгновенной изменяемостью
- Формула для подсчета числа степеней свободы плоской стержневой системы W = 3Д + 2У - 2Ш – С - Соп
- Случаи, которые могут возникать при подсчете числа степеней свободы
1.W ˃ 0 Система является геометрически изменяемой (т.к. число степеней свободы, приносимых элементами цепи, превышает число степеней свободы, выключаемых кинематическими связями. Условие геометрической изменяемости является необходимым и достаточным), статически противоречива.
2.W ˂ 0 Система является геометрически неизменяемой с избыточным числом связей, статически неопределима
3.W = 0 Система является геометрически неизменяемой с достаточным числом связей, статически определима
-Анализ геометрической структуры плоской стержневой системы заключается в последовательном рассмотрении схем соединения кинематическими связями дисков и узлов кинематической цепи конструкции между собой и с основанием.
-Изображение основных схем правильного и неправильного соединения элементов кинематической цепи:
1.Правильное а) Два диска, соединенные между собой тремя непараллельными
и не пересекающимися в одной точке стержнями, образуют ЕЖД.
б) Три диска, соединенные между собой тремя шарнирами, не лежащими на одной прямой, образуют ЕЖД.
в) Два диска, соединенный между собой при помощи шарнира и стержня, ось которого не проходит через центр шарнира, образуют ЕЖД
г) Узел, присоединенный к диску с помощью двух стержней, не лежащими на одной прямой, образуют единый жесткий диск (ЕЖД).
2.Неправильное а,б) Неправильное расположение стержней между дисками,
приводящее к возникновению мгновенного центра
в) Неправильное расположение шарниров между дисками, приводящее к возникновению мгновенного центра
г) Неправильное расположение связей между дисками, приводящее к возникновению мгновенного центра
д) Неправильное присоединение узла к диску, приводящее к возникновению мгновенного центра
-Алгоритм кинематического анализа:
1.изобразить расчетную схему конструкции в виде кинематической цепи
2.подсчитать число дисков Д, число узлов У, число шарниров Ш, число стержней внутри цепи С, число опорных стержней Соп
3.подсчитать число степеней свободы кинематической цепи W
4.если W ˃ 0, сделать вывод о геометрической изменяемости и статической противоречивости конструкции
5.если W ≤ 0, провести анализ геометрической структуры конструкции
6.сделать вывод о кинематических и статических свойствах конструкции с учетом результатов анализа геометрической структуры конструкции
2.
- Изгибающий момент, Поперечная сила, Продольная сила – внутренние усилия конструкции, которые для поперечного сечения в целом числовой мерой внутренних сил являются составляющие главного вектора и главного момента таких сил при их приведении к центру тяжести поперечного сечения.
- Изгибающий момент - момент относительно оси, параллельной оси х и проходящей через центр тяжести сечения, всех сил, приложенных слева от сечения или приложенных справа, но взятых с обратным знаком.
- Поперечная сила - сумма проекций на вертикальную ось всех сил, приложенных слева от сечения или приложенных справа, но с обратным знаком.
- Продольная сила - составляющая главного вектора по нормали к сечению.
-Особенности определения внутренних усилий в статически определимых системах:
1.независимость определения опорных реакций и внутренних усилий от перемещений, возникающих в конструкции, и размеров поперечных сечений ее конструктивных элементов.
2.внутренние силы, возникающие в элементах стержневой конструкции, с помощью метода сечений могут рассматриваться как внешние силы
3.числовой мерой внутренних сил в произвольной точке поперечного сечения конструктивного элемента являются напряжения – полные p, касательные τ и нормальные Ϭ. Напряжения численно характеризуют интенсивность внутренних сил, приходящихся на единицу площади поперечного сечения.
-Виды статически определимых систем
1.простые (будучи отделенными от опор представляют собой единый диск без внутренних связей)
2.составные (будучи отделенными от опор НЕ представляют собой единый диск без внутренних связей)
-Свойства статически определимых систем:
1.Каждой нагрузке, приложенной к конструкции, соответствует единственная система значений опорных реакций и внутренних усилий этой конструкции.
2.Нагрузка, приложенная к основному элементу составной конструкции, вызывает внутренние усилия только в этом элементе, а нагрузка, приложенная к дополнительному элементу, вызывает внутренние усилия как в нем, так и в элементах, на которые он опирается.
3.Уравновешенная нагрузка, приложенная к геометрически неизменяемой части конструкции, вызывает внутренние усилия только в этой части, а в остальных частях конструкции они равны нулю.
4.Замена нагрузки, приложенной к некоторой геометрически неизменяемой части конструкции, эквивалентной нагрузкой не изменяет внутренних усилий в остальных частях конструкции.
5.В статически определимых стержневых конструкциях не возникают внутренние усилия от температурного воздействия, осадки опор и вследствие неточностей изготовления конструктивных элементов.
-Формы определения внутренних усилий в статически определимых системах
1.аналитическая 2.графическая 3.матричная
-Статический метод определения внутренних усилий основан на использовании метода сечений и рассмотрении условий равновесия конструкции в целом или отдельных её частей.
- Кинематический метод определения внутренних усилий основан на использовании принципа возможных перемещений для несвободной механической системы.
-Дискретизация расчетной схемы конструкции предполагает ее разбиение на отдельные элементы, введение мест их соединения и выделение расчетных сечений конструкции.
- Дискретизация внешней нагрузки конструкции заключается в замене заданной нагрузки статически эквивалентной системой сосредоточенных сил, приложенных в узлах дискретной расчетной схемы.
- Матрица влияния внутреннего усилия
Матричная форма линейных соотношений имеет вид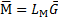 
.
Входящая в эту формулу матрица 
осуществляет линейное преобразование нагрузки 
в искомый вектор балочных изгибающих моментов 
и называется матрицей влияния изгибающих моментов
3.
-Виды подвижных нагрузок:
1.двухосная подвижная нагрузка (кары, автомобили)
2.многоосная подвижная нагрузка (одновременное движение двухосных механических экипажей, ж/д составы)
3.гусеничная нагрузка (различные виды движущихся механических экипажей на гусеничном ходу, трактор)
- Опасное положение подвижной нагрузки – положение подвижной нагрузки, при которой требуемые величины принимают экстремальные значения
-Подходы к отысканию опасных положений подвижных нагрузок:
1.первый подход основан на получении аналитических выражений, определяющих непрерывные изменения искомых величин в зависимости от положения подвижной нагрузки на конструкции. Исследуя полученные функции методами мат.анализа, можно найти их наибольшие и наименьшие значения.
2.второй подход основан на понятии линии влияния. Он справедлив только для линейно деформируемых систем, но дает для них общий метод отыскания опасных положений любых подвижных нагрузок
- Функция влияния внутреннего усилия. При движении единичной нагрузки любая величина Z (внутреннее усилие или перемещение), возникающая в конструкции, зависит только от абсциссы х и описывается некоторой функцией Z=f(х).
- Линия влияния внутреннего усилия некоторой величины Z, возникающей в определенном месте конструкции, называется график, описывающий изменение этой величины в зависимости от положения движущегося по конструкции вертикального сосредоточенного единичного груза.
- Отличия линии влияния внутреннего усилия от эпюры аналогичного внутреннего усилия:
1.эпюра некоторого внутреннего усилия описывает его изменение по длине всей конструкции, а линия влияния описывает изменение этого внутреннего усилия в одном определенном месте конструкции (опора, сечение)
2.Эпюра внутренних усилий связана с действием реальной неподвижной нагрузки, заданной в одном определенном положении, а линия влияния порождается действием искусственной подвижной нагрузки, которая может занимать различные положения на конструкции.
- Статический способ построения линий влияния внутренних усилий основан на составлении уравнений равновесия для конструкции, нагруженной в произвольном месте с абсциссой х неподвижным единичным грузом, и определении из этих уравнений внутреннего усилия как некоторой функции от х.
-Запишите функции влияния опорных реакций простой двухконсольной балки и получите с их помощью линии влияния. (УМК, стр. 60.)
-Запишите функцию влияния изгибающего момента простой двухконсольной балки в произвольном сечении пролета и получите с ее помощью линию влияния.(УМК, стр.61)
- Запишите функцию влияния изгибающего момента простой двухконсольной балки в произвольном сечении консоли и получите с ее помощью линию влияния.
-Запишите функцию влияния поперечной силы простой двухконсольной балки в произвольном сечении пролета и получите с ее помощью линии влияния.(УМК, стр. 62)
-Запишите функцию влияния поперечной силы простой двухконсольной балки в произвольном сечении консоли и получите с ее помощью линии влияния.
-Общий порядок построения линий влияния внутренних усилий кинематическим способом
1.удалить связь, линию влияния реакции которой требуется построить, и заменить удаленную связь соответствующей реакцией положительного направления. Приемами удаления связей являются отбрасывание стержня, введение в сечение шарнира или «качелей».
2.придать полученному механизму возможное отклонение, направление которого задается в соответствии с положительным направлением реакции удаленной связи.
3.выбрать специальный масштаб для отклоненного положения механизма, при котором перемещение по направлению реакции удаленной связи полагается равным 1.
- Формула для определения внутреннего усилия по линиям влияния от неподвижной сосредоточенной силы:
Пусть к конструкции приложена сосредоточенная сила Р1 на расстоянии а1 от левой опоры. Ордината линии влияния под местом приложения силы имеет некоторое значение s1. Исходя из смысла ординаты линии влияния и существования прямой пропорциональной зависимости внутреннего усилия S от силы Р1, получим следующую формулу для определения S: 
- Формула для определения внутреннего усилия по линиям влияния от неподвижной системы сосредоточенных сил:
Пусть к конструкции приложена система сосредоточенных сил Рi на расстояниях аi от левой опоры. Ординаты линии влияния под местом приложения сил имеет некоторое значение si. Исходя из принципа независимости действия сил и с учетом формулы 
получим следующую формулу для определения S: 
. 
и получим 
, где 
. Отсюда следует, что усилие S равняется: 
- Формула для определения внутреннего усилия по линиям влияния от неподвижной распределенной нагрузки постоянной интенсивности:
Пусть к конструкции на некотором участке [а,b] приложена распределенная нагрузка с переменной интенсивностью g(x). Выделим элементарный участок dx и определим для него равнодействующую нагрузки R=g(x)dx. Тогда, применяя и выполняя интегрирование на участке [а,b], получим следующую формулу для определения S: 
. При постоянной интенсивности g можно вынести за знак интеграла и тогда формула примет вид: 
.
- Формула для определения внутреннего усилия по линиям влияния от неподвижного внешнего момента:
Пусть к конструкции приложен момент М1 на расстоянии а1 от левой опоры. Представим заданный момент в виде пары вертикальных сил с плечом dx. Ординаты линии влияния под местами приложения заменяющих сил M1/dx, соответственно, имеют значения s и s+ds. Тогда, применяя , получим следующую формулу для определения S: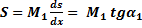 
-Формула для определения внутреннего усилия по линиям влияния от системы неподвижных внешних моментов:
Пусть к конструкции приложена система моментов Мi на расстояниях аi от левой опоры. Тангенсы углов наклона касательных к линии влияния под местами их приложения имеют значения tgα1. Исходя из принципа независимости действия сил и с учетом 
получим следующую формулу для определения S:
. 
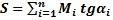
- Формула для определения max и min значений внутренних усилий по линиям влияния от временной нагрузки
-Связь линии влияния внутреннего усилия с матрицей влияния этого усилия:
С помощью линий влияния внутренних усилий можно формировать матрицы влияния этих усилий по строкам. Использование единичных эпюр внутренних усилий позволяет формировать матрицы влияния по столбцам.
4.
-Деформация конструкции – изменение формы и размера конструкции при приложении к ним внешних воздействий.
- Дифференциальные количественные характеристики деформации конструкции описывают происшедшие изменения формы и размеров конструкции в окрестности ее произвольной точки (относительной линейной деформацией ε и углом сдвига ϒ)
- Интегральные количественные характеристики деформации конструкции описывают происшедшие изменения формы и размеров конструкции в целом (линейное и угловое перемещения).
- Жесткость конструкции зависит от применяемого конструкционного материала, жесткости конструктивных элементов и способов соединения этих элементов между собой.
- Жесткость конструкционного материала характеризуется отношением жесткости поперечного сечения к длине элемента и называется его погонной жесткостью при изгибе, растяжении-сжатии или сдвиге.
-Подходы к определению перемещений:
1.один подход связан с определением малых перемещений, и он справедлив для жестких конструкций. Такие конструкции обычно относятся к линейно-деформируемым системам. Согласно этому подходу определяются перемещения, которые малы по сравнению с размерами самой конструкции.
2.второй подход позволяет определять большие перемещения, и он справедлив для гибких конструкций. Такие конструкции обычно относятся к геометрически нелинейным системам. Согласно этому подходу определяются перемещения, которые не малы по сравнению с размерами самой конструкции.
-Цели определения перемещений конструкции:
1.для оценки пригодности конструкций к нормальной эксплуатации
2.
-Если к конструкции по направлению номер j приложить безразмерную силу 
= 1, то возникающие в конструкции перемещения по указанным выше направлениям называют единичными перемещениями. Такие перемещения обозначаются 
и их индексы указывают те же направления, что и для частичных перемещений 
. Единичные перемещения подразделяются на собственные и побочные.
-Законом Гука для конструкции называется соотношение 
, согласно которому полное перемещение 
является линейной функцией действующих сил 
.
-Входящие в 
и единичные перемещения играют роль коэффициентов пропорциональности между силами и перемещениями. Они позволяют количественно оценивать способность конструкции получать перемещения по определенному направлению и поэтому называются коэффициентами податливости.
- Применим к каждому полному перемещению конструкции.
. 
……………………………………..
. 
Входящие в полученные линейные соотношения коэффициенты податливости образуют квадратную матрицу, которая называется матрицей податливости конструкции. Тогда матричная запись имеет вид 
.
. 
-Соотношения …………………………………….., согласно которым действующие на конструкцию силы являются
. 
линейными функциями её полных перемещений, являются другой формой обобщенного закона Гука. Входящие в эти соотношения коэффициенты пропорциональности 
количественно характеризуют способность конструкции сопротивляться возникновению перемещений по определенному направлению, называются коэффициентами жесткости и образуют матрицу жесткости конструкции (). Матричная запись имеет вид 
.
- В общем случае при статическом нагружении стержневой конструкции на нее действует некоторая совокупность сосредоточенных сил, моментов и распределенных нагрузок. Если составляющие этой совокупности нагрузок изменяются пропорционально одному параметру Р, то она называется обобщенной силой.
-Под обобщенным перемещением понимают некоторую геометрическую величину, связанную с деформированным состоянием конструкции, произведение которой на параметр обобщенной силы позволяет вычислить действительную или возможную работу заданной совокупности нагрузок по одночленным формулам вида А = 
или А'= РΔ'к .
- Принцип возможных перемещений для деформируемой системы. Согласно этому принципу, если деформируемая система находится в равновесии, то сумма работ всех действующих сил, включая и внутренние силы, на возможных перемещениях системы от положения равновесия равняется нулю.
- Формула Максвелла-Мора для произвольной плоской стержневой конструкции
- Формула Максвелла-Мора для балок и плоских рам
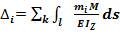
-Формула Максвелла-Мора для арок и комбинированных систем
-Формула Максвелла-Мора для ферм
-Формула для определения перемещений от действия температуры в статически определимой плоской стержневой конструкции
-Формула для определения перемещений от действия осадки опор в статически определимой плоской стержневой конструкции
-Правило Верещагина. Определенный интеграл от произведения двух функций, одна из которых линейная, а вторая нелинейная, равняется произведению площади графика нелинейной функции на ординату графика линейной функции, расположенную под центром тяжести площади графика нелинейной функции. В случае, если вторая функция тоже является линейной, то при пользовании формулой 
безразлично, площадь графика какой функции следует вычислять. Правило знаков. Если график нелинейной функции и ордината графика линейной функции, расположены по одну сторону оси, то результат положительный, в противном случае он отрицательный.
- Границы применения правила Верещагина:
1. нелинейная + линейная
2. линейная + линейная
3. нелинейная + нелинейная (нельзя!)
-Теорема о взаимности работ. Возможная работа внешних сил i-того состояния конструкции на перемещениях, вызванных внешними силами k-того состояния, равняется возможной работе внешних сил k-того состояния конструкции на перемещениях, вызванных внешними силами i-того состояния. (
)
-Теорема о взаимности перемещений. Побочные единичные перемещения конструкции с различным порядком расположения одинаковых индексов равны между собой. (
)
5.
-Реальная ферма представляет собой геометрически неизменяемую стержневую конструкцию с жестким соединением прямолинейных стержней в узлах.
-Расчетная схема фермы – это система, полученная при замене жестких узлов шарнирами
- При узловой нагрузки в прямолинейных стержнях фермы не возникают изгибающие моменты и поперечные силы, а продольные силы постоянны по длине каждого стержня.
- При узловой нагрузки в криволинейных стержнях фермы изгибающие моменты и поперечные силы не равны нулю, а продольные силы переменны по длине стержня.
- При внеузловой нагрузки в прямолинейных стержнях фермы изгибающие моменты и поперечные силы не равны нулю, а продольные силы переменны по длине стержня.
-Термины и обозначения:
Элементы фермы, расположенные по ее внешнему контуру, образуют ее пояса (верхний О и нижний U).
Участок пояса между смежными узлами называется панелью этого пояса.
Элементы, расположенные внутри контура и соединяющие пояса, образуют решетку фермы.
Наклонные элементы решетки называются раскосами (D). Различают восходящие и нисходящие раскосы.
Вертикальные элементы решетки называются стойками (V). Различают основные стойки, дополнительные стойки и опорные стойки.
Пролетом фермы называется расстояние по горизонтали между осями ее опор (l).
Высотой фермы называется расстояние по вертикали между центрами наиболее удаленных друг от друга узлов верхнего и нижнего поясов (h).
Длиной панели пояса называется расстояние по горизонтали между смежными узлами этого пояса (и).
- Классификация ферм
1.по назначению (мостовые фермы, стропильные фермы, крановые фермы)
2.по очертанию внешнего контура (фермы с параллельными поясами, фермы с полигональным или ломаным очертанием обоих или одного из них)
3.по системе решетки (простой и сложной решетками)
4.по схеме опирания (безраспорными и распорными)
5.по способу образования геометрической структуры (простые, сложные и составные фермы)
-Разновидности статического метода определения внутренних усилий в стержнях простых ферм при узловом нагружении:
1.метод вырезания узлов
2.метод рассечения на крупные части
3.комбинированный метод
-Метод вырезания узлов. В основе метода лежит использование уравнений равновесия системы сходящихся сил и применение их к узлам фермы, мысленно вырезанным из нее сквозными сечениями. Для каждого узла фермы можно составить по два независимых уравнения равновесия.
- Метод рассечения на крупные части. В основе метода лежит использование уравнений равновесия системы сил, произвольно расположенных на плоскости, и применение их к одной из частей фермы, полученной при ее мысленном рассечении через любые три стержня. Оси таких стержней не должны пересекаться в одной точке.
- Комбинированный метод. Метод используется для определения продольных сил в стержнях фермы, когда их нельзя найти сразу ни методом вырезания узлов, ни методом рассечения на крупные части. Суть метода заключается в одновременном использовании рассмотренных двух методов для отыскания требуемой продольной силы.
- Нулевые стержни фермы – это стержни, в которых продольные силы при данной схеме узловой нагрузки тождественно равны нулю.
- Признаки нулевых стержней.
1.в ненагруженном двухстержневом узле фермы оба стержня нулевые
2.в двухстержневом узле фермы, нагруженном силой вдоль оси одного из стержней, другой стержень нулевой
3.в ненагруженном трехстержневом узле фермы, в котором оси двух стержней направлены по одной прямой, третий стержень нулевой.
6.
-Арка представляет собой кривой брус, опертый на две опоры, исключающие горизонтальные перемещения опорных сечений.
-Разновидности арок по схеме опирания:
1.бесшарнирная арка (кривой брус, опирающийся на две защемляющие неподвижные опоры)
2.двухшарнирная арка (кривой брус, опирающийся на две шарнирно неподвижные опоры)
3.двухшарнирная арка с затяжкой (кривой брус с присоединенным к нему горизонтальным стержнем, опирающийся на шарнирно неподвижную и шарнирно подвижную опоры.)
4.трехшарнирная арка (два кривых бруса, соединенных шарниром и опирающихся на две шарнирно-неподвижные опоры)
5.трехшарнирная арка с затяжкой (два кривых бруса, соединенных шарниром и затяжкой и опирающихся на шарнирно неподвижную и шарнирно подвижную опоры)
-Термины и обозначения:
Опорные сечения арки А и В принято называть пятовыми сечениями или пятами арки.
Наиболее удаленное сечение кривого бруса С от линии, соединяющий центры опор, называется замковым сечением или замком арки.
В случае, если в названных сечениях располагаются шарниры, то они, соответственно, называются пятовыми и замковыми шарнирами.
Расстояние между пятами арки называется пролетом арки (2L).
Расстояние между пятой и замком арки называется стрелой подъема арки (f).
Важной характеристикой арки является соотношение f/2L, которое зависит от назначения сооружения и может изменяться в широких пределах. В зависимости от его величины различают пологие, обычные и крутые арки.
-Формулы для определения опорных реакций трехшарнирной арки при действии вертикальной нагрузки
Для определения составляющих опорных реакций арки и сопоставления их с опорными реакциями балки составим для каждой конструкции уравнения моментов относительно их правых и левых опор. Вертикальные составляющие опорных реакций трехшарнирной арки равны опорным реакциям соответствующей балки. Составим для арки сумму проекций сил на ось х и найдем горизонтальные составляющие опорных реакций. Горизонтальная составляющая Н опорных реакций трехшарнирной арки называется ее распором.
Для определения распора трех шарнирной арки рассматривается равновесие одной из полуарок и используется уравнение моментов относительно замкового шарнира.
- Формулы для определения внутренних усилий трехшарнирной арки при действии вертикальной нагрузки
(УМК, стр.118)
-Сравнение внутренних усилий трехшарнирной арки и простой балки при действии вертикальной нагрузки
(УМК, стр.119)
-Преимущества арки перед балкой. (УМК, стр.119)