Случайным называется событие, исход которого при определенном комплексе условий невозможно предсказать заранее.
Когда речь идет об эксперименте, подразумевается, что он имеет определенные исходы. Список этих исходов часто бывает довольно небольшим. Например, при бросании игральной кости их шесть. При бросании монеты их всего два.
Случайная величина – величина, которая может принимать какое-либо значение из установленного множества и с которой связано вероятностное распределение.
Случайная величина может быть дискретной или непрерывной.
Дискретная случайная величина - может принимать значения только из конечного или счетного множества действительных чисел.
Непрерывная случайная величина – может принимать любые значения конечного или бесконечного интервала.
Эксперимент и его исходы часто имеют определенные числовые характеристики. Именно наличие такого рода числовых характеристик и дает основания для использования математических методов при изучении случайных событий.
Если зафиксировать уровни контролируемых факторов и провести n измерений отклика X, то в результате будет получен ряд близких,но отличных друг от друга значений xi, (i=1,2,…,n), где xi - i-ое измерение величины X, x1,x2,…xn – реализация случайной величины X.
Одной из важнейших числовых характеристик случайного события является его вероятность, которая является некоторым числом, сопоставляемым данному случайному событию. Нужно понимать, что это – фундаментальная характеристика и потому простого определения, применимого ко всем случайным событиям, просто не может быть (как нет, например, универсального определения для понятия «событие»).
В некоторых простейших случаях такое определение может быть, конечно, дано. В элементарных учебниках по теории вероятностей часто ограничиваться «классическим» определением, которое основано на хорошо известной простой схеме. В этой схеме для определения вероятности некоторого случайного события A выделяется некоторое (конечное) множество исходов, которые полагаются (или предполагаются) равновероятными. Обозначим число этих исходов через n. Далее, устанавливается, что заданному событию A благоприятствуют определенное число, скажем m, из этих n исходов.
Тогда полагают по определению, что частотой реализации события А
w=m/n.
Вероятность p(A) случайного события A - число от нуля до единицы, которое представляет собой предел частоты реализации события А при неограниченном числе повторений одного и того же комплекса условий.
Для дискретной случайной величины можно указать вероятность, с которой она принимает каждое из своих возможных значений конечного или счетного множества действительных чисел. Для непрерывной случайной величины задают вероятность ее попадания в один из заданных интервалов области ее определения, поскольку вероятность того, что она примет какое-то определенное значение, стремится к нулю.
Случайные величины можно задавать разными способами. Дискретные случайные величины обычно задаются своим законом распределения в табличном или графическом виде. Каждому возможному значению x1, x2,... случайной величины X сопоставляется вероятность p1,p2,... этого значения. В результате образуется таблица, состоящая из двух строк:
x1 x2 x3...
p1 p2 p3...
Это и есть закон распределения случайной величины, под которым понимают связь между возможными значениями случайной величины и соответствующими им вероятностями.
Непрерывные случайные величины законом распределения в виде таблицы задать невозможно, так как по определению их значения невозможно перенумеровать. Однако для непрерывных случайных величин есть другой способ задания (применимый, кстати, и для дискретных величин) – это функция распределения. Обычно используется два способа описания распределений вероятностей случайных величин: интегральный (с помощью функции распределения) и дифференциальный (задается плотностью распределения).
Функция распределения F(x) определяет для всех действительных x вероятность того, что случайная величина X принимает значение не больше, чем x:
F(x)=P(X<x). (5.1)
Геометрически равенство (5.1) можно истолковать так: F(x) есть вероятность того, что случайная величина X примет значение, которое изображается точкой, лежащей левее точки x, т.е. случайная точка X попадает на интервал (-∞, x), см. рис.5.1.
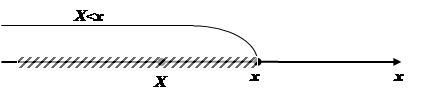
Рисунок 5.1 – К геометрическому истолкованию формулы (5.1)
Функция распределения F(x) имеет следующие свойства:
1. F(x) принимает значения от 0 до 1: 0≤ F(x)≤1.
2. Ее ордината, соответствующая произвольной точке x1, представляет собой вероятность того, что случайная величина X будет меньше, чем x1, т.е. F(x1)=P(X<x1).
3. Функция распределения стремится к нулю при неограниченном уменьшении x и стремится к единице при неограниченном возрастании x, т.е.
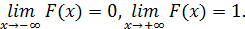
4. Функция распределения представляет собой монотонно возрастающую кривую, т.е. F(x1)> F(x2), если x1 > x2.
5. Ее приращение на произвольном интервале (x1,x2) равно вероятности того, что случайная величина X попадет в данный интервал:
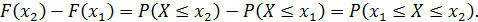
Рисунок 5.2 – К свойству 5.
Часто вместо функции распределения удобно использовать другую функцию – плотность распределения случайной величины X. Ее еще иногда называют дифференциальной функцией распределения. Плотность распределения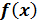 
это первая производная (если она существует) функции распределения и отражает скорость изменения 
:
.
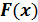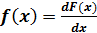Плотность функции распределения 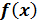имеет следующие свойства:
1. Плотность распределения вероятностей является неотрицательной функцией, т.е.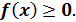 
Это свойство является следствием того, что функция 
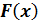есть неубывающая функция.
2. Функция распределения вероятностей случайной величины равна X равна определенному интегралу от плотности распределения вероятностей в пределах от -∞ до x:
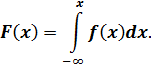
3. Вероятность события, состоящего в том, что случайная величина X примет значение, заключенное в интервале (x1, x2), равна определенному интегралу от плотности распределения вероятностей на этом интервале:
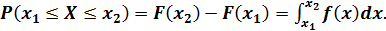
Геометрически эта вероятность равна площади заштрихованной фигуры, ограниченной сверху кривой распределения f(x) и опирающейся на отрезок [x1,x2] (рис.5.3).
Рисунок 5.3 – Геометрическая интерпретация свойства 3.
4. Интеграл плотности распределения на бесконечно большом интервале (-∞,+∞) равен единице:
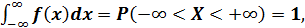так как попадание случайной величины на интервал 
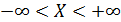есть достоверное событие.
В большинстве случаев при обработке экспериментальных данных, основываясь на свойствах исследуемой случайной величины, удается записать функцию ее распределения (плотность распределения) с точностью до некоторых неизвестных параметров. Так, для случайной величины, которая удовлетворяет нормальному закону распределения (закону Гаусса), функция распределения записывается в виде:
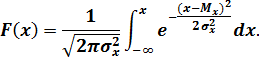
В этом случае константы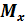 
, 
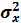являются параметрами распределения и определяют двухпараметрический закон распределения.
Параметр распределения – постоянная величина, от которой зависит функция распределения.
Следовательно, если установлено, что случайная величина не противоречит тому или иному закону распределения, то для того, чтобы однозначно охарактеризовать эту случайную величину, достаточно знать параметры ее распределения. Так, для нормального закона параметрами распределения являются 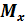- математическое ожидание (характеризующее центр рассеивания) и 
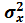- дисперсия (характеризует степень рассеивания).