1. Угол между касательной к эллипсу и фокальным радиусом r1 равен углу между касательной и фокальным радиусом r2 (Рис. 2, точка М3).
2. Уравнение касательной к эллипсу в точке М с координатами (xM, yM):
| 1 = | xxM | + | yyM |
| a2 | b2 |
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через центр эллипсa. (Это свойство дает возможность построением с помощью циркуля и линейки получить центр эллипса.)
4. Эволютой эллипсa есть астероида, что растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами F1 и F2 у треугольник ∆ ABC, то будет выполнятся следующее соотношение:
| 1 = | F1A ∙ F2A | + | F1B ∙ F2B | + | F1C ∙ F2C |
| CA ∙ AB | AB ∙ BC | BC ∙ CA |
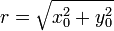 , целиком принадлежит этой поверхности.
Если в некоторой декартовой прямоугольной системе координат поверхность S задана уравнением F(x2+y2,z)=0, то S — поверхность вращения вокруг оси OZ.
Эллипсоид
, целиком принадлежит этой поверхности.
Если в некоторой декартовой прямоугольной системе координат поверхность S задана уравнением F(x2+y2,z)=0, то S — поверхность вращения вокруг оси OZ.
Эллипсоид
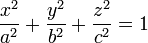 Эллипсоид – ограниченная поверхность.
2. Эллипсоид обладает:
центральной симметрией относительно начала координат,
осевой симметрией относительно координатных осей,
плоскостной симметрией относительно начала координат.
3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.
Однополостной гиперболоид.
Эллипсоид – ограниченная поверхность.
2. Эллипсоид обладает:
центральной симметрией относительно начала координат,
осевой симметрией относительно координатных осей,
плоскостной симметрией относительно начала координат.
3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.
Однополостной гиперболоид.
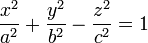 1. Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
2. Однополостной гиперболоид обладает:
центральной симметрией относительно начала координат,
осевой симметрией относительно всех координатных осей,
плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.
Двуполостной гиперболоид
1. Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
2. Однополостной гиперболоид обладает:
центральной симметрией относительно начала координат,
осевой симметрией относительно всех координатных осей,
плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.
Двуполостной гиперболоид
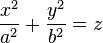 1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.
2. Эллиптический параболоид обладает:
осевой симметрией относительно оси Oz,
плоскостной симметрией относительно координатных осей Oxz и Oyz.
3. В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола.
1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.
2. Эллиптический параболоид обладает:
осевой симметрией относительно оси Oz,
плоскостной симметрией относительно координатных осей Oxz и Oyz.
3. В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола.
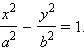 Свойство 1.
Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (–a; 0), которые называются вершинами гиперболы.
Свойство 2.
Гипербола имеет две взаимно перпендикулярные оси симметрии.
Свойство 3.
Гипербола имеет центр симметрии.
Свойство 4.
Гипербола пересекается с прямой y = kx при
Свойство 1.
Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (–a; 0), которые называются вершинами гиперболы.
Свойство 2.
Гипербола имеет две взаимно перпендикулярные оси симметрии.
Свойство 3.
Гипербола имеет центр симметрии.
Свойство 4.
Гипербола пересекается с прямой y = kx при 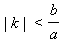 в двух точках.
Если
в двух точках.
Если 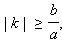 то общих точек у прямой и гиперболы нет.
Асимптоты гиперболы – это прямые, проходящие через центр гиперболы. Гипербола приближается к асимптотам, но никогда не пересекает (и даже не касается) их. Асимптоты определяют характер гиперболы при удалении от начала координат. Можно доказать, что если точка гиперболы неограниченно удаляется от начала координат, то расстояние от неё до одной из асимптот стремится к нулю. Асимптоты позволяют более точно изображать гиперболу. Для этого берут прямоугольник с вершинами (а, b), (а, —b), (—а, b), (—а, —b) и проводят прямые, продолжающие его диагонали. Уравнения этих прямых: y = +-(b/a)x, то есть это и есть асимптоты. Затем рисуют гиперболу, начиная от вершин и приближаясь к асимптоте по мере удаления от начала координат.
то общих точек у прямой и гиперболы нет.
Асимптоты гиперболы – это прямые, проходящие через центр гиперболы. Гипербола приближается к асимптотам, но никогда не пересекает (и даже не касается) их. Асимптоты определяют характер гиперболы при удалении от начала координат. Можно доказать, что если точка гиперболы неограниченно удаляется от начала координат, то расстояние от неё до одной из асимптот стремится к нулю. Асимптоты позволяют более точно изображать гиперболу. Для этого берут прямоугольник с вершинами (а, b), (а, —b), (—а, b), (—а, —b) и проводят прямые, продолжающие его диагонали. Уравнения этих прямых: y = +-(b/a)x, то есть это и есть асимптоты. Затем рисуют гиперболу, начиная от вершин и приближаясь к асимптоте по мере удаления от начала координат.
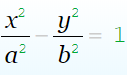 гиперболический цилиндр
гиперболический цилиндр
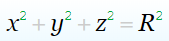 сфера
сфера
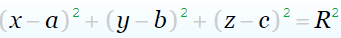 сфера, центр которой не из центра системы координат
сфера, центр которой не из центра системы координат
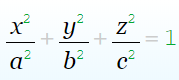 ЭЛЛИПСОИД
ЭЛЛИПСОИД
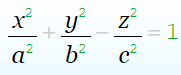 ОДНОПОЛОСТНЫЙ ГИПЕРБОЛОИД
ОДНОПОЛОСТНЫЙ ГИПЕРБОЛОИД
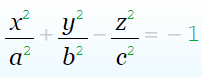 ДВУПОЛОСТНЫЙ ГИПЕРБОЛОИД
ДВУПОЛОСТНЫЙ ГИПЕРБОЛОИД
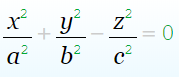 КОНУС ВТОРОГО ПОРЯДКА
КОНУС ВТОРОГО ПОРЯДКА
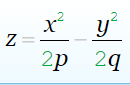 ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД
ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД
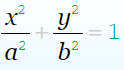 ЭЛЛИПТИЧЕСКИЙ ЦИЛИНДР
ЭЛЛИПТИЧЕСКИЙ ЦИЛИНДР
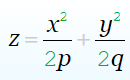 ЭЛЛИПТИЧЕСКИЙ ПАРАБОЛОИД
ЭЛЛИПТИЧЕСКИЙ ПАРАБОЛОИД
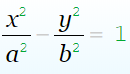 ГИПЕРБОЛИЧЕСКИЙ ЦИЛИНДР
метод исследования
Просто представляешь один из параметров, допустим z, как какое-то число h, которое лежит на промежутке от 0 до c (поскольку там z^2/c^2). И просто подставляешь в уравнение. Далее переносишь результат за знак = и смотришь что за фигура такая получилась. Она и есть сечение по оставшимся осям.
Для элипса там 2 случая. h=c и h<c. В первом случае это будет точка (0 0), а в другом элипс будет увеличиваться и достигнет максимальных размеров элипса.
ГИПЕРБОЛИЧЕСКИЙ ЦИЛИНДР
метод исследования
Просто представляешь один из параметров, допустим z, как какое-то число h, которое лежит на промежутке от 0 до c (поскольку там z^2/c^2). И просто подставляешь в уравнение. Далее переносишь результат за знак = и смотришь что за фигура такая получилась. Она и есть сечение по оставшимся осям.
Для элипса там 2 случая. h=c и h<c. В первом случае это будет точка (0 0), а в другом элипс будет увеличиваться и достигнет максимальных размеров элипса.
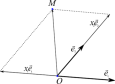 Декартовая СК: n=α Определение. Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости. 1.) ех= 1; к=1, …, n 2.) еi ej Вектор х = x1i+x2j+x3k (х1, х2, х3 - векторы) IхI(вектор)= √ x1i+x2j+x3k Координаты точки. Вектор OM называется радиусом-вектором точки M. Координатами точки M в системе координат (O; b1, b2, b3) называются координаты ее в некоторой радиуса-вектора в базисе (b1, b2, b3). Тот факт, что точка M в системе координат имеет координаты (a1, a2, a3), будем обозначать так: M(a1, a2, a3). Координаты точки на плоскости определяются аналогично координатам точки в пространстве. чтобы найти координаты вектора, надо из координат его конца вычесть координаты его начала: OМ (x2−x1,y2−y1). Угол между векторами:
Декартовая СК: n=α Определение. Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости. 1.) ех= 1; к=1, …, n 2.) еi ej Вектор х = x1i+x2j+x3k (х1, х2, х3 - векторы) IхI(вектор)= √ x1i+x2j+x3k Координаты точки. Вектор OM называется радиусом-вектором точки M. Координатами точки M в системе координат (O; b1, b2, b3) называются координаты ее в некоторой радиуса-вектора в базисе (b1, b2, b3). Тот факт, что точка M в системе координат имеет координаты (a1, a2, a3), будем обозначать так: M(a1, a2, a3). Координаты точки на плоскости определяются аналогично координатам точки в пространстве. чтобы найти координаты вектора, надо из координат его конца вычесть координаты его начала: OМ (x2−x1,y2−y1). Угол между векторами: 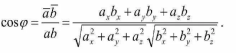
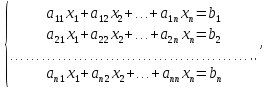 Причем r(A)=r(B)=n, т. е. система имеет единственное решение. Запишем систему в матричном виде: A*X=B, где
Причем r(A)=r(B)=n, т. е. система имеет единственное решение. Запишем систему в матричном виде: A*X=B, где
 ,
, 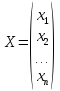 ,
, 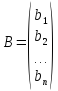 .
Умножим обе части матричного уравнения слева на матрицу A−1A−1 * A*X=B Так как A−1 * A=E, то получаем E*X= A−1 * B, откуда получаем равенство для нахождения неизвестных X= A−1 * B
.
Умножим обе части матричного уравнения слева на матрицу A−1A−1 * A*X=B Так как A−1 * A=E, то получаем E*X= A−1 * B, откуда получаем равенство для нахождения неизвестных X= A−1 * B
 элемента
элемента  определителя n-го порядка
определителя n-го порядка  называется определитель (n-1) -го порядка, полученный из определителя n-го порядка
называется определитель (n-1) -го порядка, полученный из определителя n-го порядка  вычеркиванием i- й строки и j-го столбца, на пересечении которых стоит элемент
вычеркиванием i- й строки и j-го столбца, на пересечении которых стоит элемент 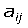 .Алгебраическое дополнение
.Алгебраическое дополнение 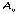 элемента
элемента  определителя
определителя 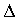 равно минору этого элемента
равно минору этого элемента 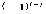 , т.е.
, т.е. 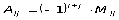 Теорема Лапласа: определитель квадратной матрицы равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения (разложение по элементам какого – либо ряда)
Теорема Лапласа: определитель квадратной матрицы равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения (разложение по элементам какого – либо ряда) 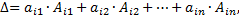 где
где 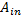 -алгебраические дополнения элементов строк матрицы. Или
-алгебраические дополнения элементов строк матрицы. Или 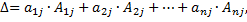 где
где 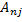 -алгебраические дополнения элементов столбцов матрицы. Алгебраическим дополнением
-алгебраические дополнения элементов столбцов матрицы. Алгебраическим дополнением  элемента определителя называется его минор, взятый со своим знаком, если сумма индексов
элемента определителя называется его минор, взятый со своим знаком, если сумма индексов 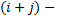 число четное, и с противоположным знаком, если сумма индексов (
число четное, и с противоположным знаком, если сумма индексов (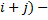 число нечетное
число нечетное