Медленными считаются движения, совершаемые со скоростью, гораздо меньшей скорости света? »c
Для количественной характеристики процесса движения тела вводится понятие скорости движения.
Мгновенной скоростью поступательного движения тела в момент времени t называется отношение очень малого перемещения?S к малому промежутку времени?t за которое произошло это перемещение:
? =?S/?t
Мгновенная скорость – векторная величина.
При последовательном уменьшении длительности промежутка времени t направление вектора перемещения приближается к касательной траектории движения, через которую проходит тело в момент времени t. Поэтому вектор скорости V лежит на касательной к траектории движения тела и направлен в сторону движения тела.
1 м/с равен скорости прямолинейно и равномерно движущейся точки, при которой точка за время 1 с перемещается на расстояние 1 м. Покой и движение тела относительны, скорость движения тела зависит от выбора системы отсчета. Изменение скорости движения тела может происходить только при действии силы, т. е. в результате взаимодействия с другими телами. Если на тело массой m в течение времени t действует сила F и скорость его движения изменяется от до, то ускорение движения тела равно:

На основании второго закона Ньютона для силы можно написать выражение:
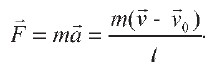
Из этого равенства следует, что:
Физическая величина, равная произведению силы F на время t ее действия, называется импульсом силы. Имеется физическая величина, одинаково изменяющаяся у всех тел под действием одинаковых сил, если время действия силы одинаково.
Эта физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела или количеством движения. Изменение импульса тела равно импульсу силы, вызывающей это изменение. Импульс тела является количественной характеристикой поступательного движения тел. В замкнутой инерциальной системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой.
Пусть на тело массой m действует постоянная сила F и векторы силы F и перемещения направлены вдоль одной прямой в одну сторону. Работа силы в этом случае определяется как A = Fs. Модуль силы по второму закону движения равен F = ma, а модуль перемещения при равноускоренном прямолинейном движении связан с модулями начальной и конечной скорости и ускорения выражением:

Отсюда для работы получаем:

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.
Тогда выражение для работы можно записать в виде:
A = Ek2 – Ek1
ПОНЯТИЕ ЭНТРОПИИ
Одним из важных законов термодинамики считается закон энтропии.
Понятие энтропии характеризует ту часть полной энергии системы, которая не может быть использована для производства работы. Поэтому в отличие от свободной энергии она представляет собой деградированную, отработанную энергию. Если обозначить свободную энергию через F, энтропию через S, то полная энергия системы Е будет равна Е = F + ВТ, где Т – абсолютная температура по Кельвину.
Согласно второму закону термодинамики энтропия в замкнутой системе постоянно возрастает и в конечном счете стремится к своему максимальному значению. Следовательно, по степени возрастания энтропии можно судить об эволюции замкнутой системы, а тем самым и о времени ее изменения. Так впервые в физическую науку были введены понятия времени и эволюции, связанные с изменением систем. Но понятие эволюции в классической термодинамике рассматривается совсем иначе, чем в общепринятом смысле. Это стало вполне очевидным после того, когда немецкий ученый Л. Баяьцман (1844–1906) стал интерпретировать энтропию как меру беспорядка (хаоса) в системе.
Таким образом, второй закон термодинамики можно было теперь сформулировать так: замкнутая система, предоставленная самой себе, стремится к достижению наиболее вероятного состояния, заключающегося в ее максимальной дезорганизации. Хотя чисто формально дезорганизацию можно рассматривать как самоорганизацию с отрицательным знаком или самодезорганизацию, тем не менее такой взгляд ничего общего не имеет с содержательной интерпретацией самоорганизации как процесса становления качественно нового, более высокого уровня развития системы. Но для этого необходимо было отказаться от таких далеко идущих абстракций, как изолированная система и равновесное состояние.
Между тем классическая термодинамика именно на них как раз и опиралась и поэтому рассматривала, например, частично открытые системы или находящиеся вблизи от точки термодинамического равновесия как вырожденные случаи изолированных равновесных систем.
Наиболее фундаментальным из таких понятий, как уже отмечалось выше, стало понятие открытой системы, которая способна обмениваться с окружающей средой веществом, энергией и информацией. Поскольку между веществом и энергией существует взаимосвязь, можно сказать, что система в ходе своей эволюции производит энтропию, которая, однако, не накапливается в ней, а удаляется и рассеивается в окружающей среде. Вместо нее из среды поступает свежая энергия и именно вследствие такого непрерывного обмена энтропия системы может не возрастать, а оставаться неизменной или даже уменьшаться. Отсюда становится ясным, что открытая система не может быть равновесной, потому ее функционирование требует непрерывного поступления энергии и вещества из внешней среды, вследствие чего неравновесие в системе усиливается. В конечном итоге прежняя структура разрушается. Между элементами системы возникают новые когерентные, или согласованные, отношения, которые приводят к кооперативным процессам. Так, схематически могут быть описаны процессы самоорганизации в открытых системах, которые связаны с диссипацией, или рассеянием, энтропии в окружающую среду.