При рассмотрении уравнений движения вязкой жидкости (уравнений Навье-Стокса) отмечалось, что интегрирование их в большинстве случаев связано с непреодолимыми математическими трудностями. Однако известны и исключения. К числу их относится ламинарное течение между параллельными пластинами, одна из которых движется с какой-то скоростью u. Это так называемое течение Куэтта.
Закономерности ламинарного течения в трубах можно получить путем прямого интегрирования уравнений Навье-Стокса [42]. В данном случае мы воспользуемся другим способом, позволяющим получить более ясные физические представления.
|
Рисунок 45 – Ламинарное течение в горизонтальной трубе
Рассматриваем установившееся ламинарное течение в горизонтальной трубе, происходящее под действием постоянного перепада давления. Радиус трубопровода - R. Двумя сечениями, отстоящими на расстоянии l друг от друга, выделим отсек трубопровода, и в нем цилиндр радиуса r. Составим уравнение движения. Так как течение установившееся, то сумма проекций на ось всех сил, действующих на цилиндр, должна быть равна нулю. Другими словами, активные силы, приводящие частицы жидкости в движение, должны быть равны силам сопротивления.
Активные силы: 
.
Силы сопротивления: 
.
Таким образом, 
и
(3.40)
Из (3.40), в частности, следует, что касательные напряжения изменяются вдоль радиуса по линейному закону. С другой стороны, по Ньютону касательные напряжения
(3.41)
Знак «минус» потому, что направления отсчета y и r противоположны.
Приравнивая (3.40) и (3.41), получаем
(3.42)
Либо после разделения переменных
(3.43)
и после интегрирования
(3.45)
Произвольную постоянную интегрирования находим из граничных условий:
при 
(условие прилипания), и
Следовательно,
(3.46)
либо
(3.47)
Максимальная скорость движения частиц будет на оси трубы, т.е. при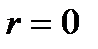 
, а ее величина
(3.48)
Подставляя (3.48) в (3.47) получим
(3.49)
Из чего следует, что в поперечном сечении трубы скорости распределены по параболическому закону, т.е. эпюра скорости представляет собой параболоид вращения.
Выражение (3.49) можно представить в виде
(3.50)
Из чего следует, что отношение скорости в любой точке к скорости на оси не зависит от расхода, рода жидкости и материала стенок трубы: при всех значениях одинаково.
Определим расход, протекающий через трубопровод. При введении понятия о средней скорости было показано, что
(3.51)
где 
- уравнение эпюры скорости.
Воспользуемся (3.46), что дает
(3.52)
Выполнив интегрирование и имея в виду (3.48), можно получить
Из чего следует, что
(3.53)
Раскрывая значение 
по (3.48), получаем выражение для определения потерь давления при ламинарном режиме течения в круглой трубе
(3.54)
Либо, заменяя радиус диаметром,
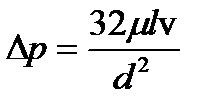(3.55)
Полученное соотношение носит название формулы Хагена-Пуазейля. Для потерь напора с учетом того, что 
, формула принимает вид
(3.56)
Важнейший вывод, следующий из этого соотношения, можно сформулировать так: потери давления (напора) при ламинарном течении в круглых трубах линейно зависят от средней скорости.
Выполним некоторые формальные преобразования формулы Хагена-Пуазейля, которые окажутся полезными в дальнейшем. Умножим числитель и знаменатель (3.56) на 
,что дает
(3.57)
Таким образом, можем записать, что в формуле 
при ламинарном течении 
.
3.4 Методика расчета малонапорной гидротурбины
3.4.1. Численное исследование характеристик направляющих лопастей гидротурбины
При работе гидравлической турбины возникает силовое взаимодействие между потоком жидкости и рабочим колесом, а также между потоком и лопастями гидротурбины. Это взаимодействие проявляется в возникновении соответствующих сил и моментов. Как показывают многочисленные исследования движение потока в прямоточной турбине можно представить как турбулентное вихревое течение жидкости в трубе.
Величины этих сил и моментов существенны для конструкции турбин, так как, не зная их, невозможно рационально спроектировать их основные узлы. Они в дополнение к энергетическим и кавитационным показателям характеризуют гидравлические качества турбины.
Зависимости величин усилий и моментов от режима работы турбины, от кривизны лопастей принято называть силовыми характеристиками. На силовых характеристиках для всего диапазона эксплуатации турбин указывают величины сил и моментов относительно оси поворота, действующих на лопастные системы. Пространственный характер потока, количество и взаимное влияние элементов подвода (спиральной камеры, колонн статора) и отсутствие ЭВМ большой мощности долгие годы, вплоть до настоящего времени, приводили к убеждению, что определить величину усилия, и особенно величину момента, действующих на поверхность лопастей, теоретическим путем с достаточной для практики точностью невозможно. Единственным надежным путем определения силовых характеристик турбины являлся физический эксперимент. Однако его выполнение весьма трудоемко, дорого и длительно. В условиях рыночной экономики его необходимо заменить вычислительным.
Современное состояние численных методов расчета пространственного поля скоростей в проточной части гидротурбины, технических параметров ЭВМ и программного обеспечения позволяет отказаться от традиционных методов определения силовых характеристик и заменить физический эксперимент вычислительным.
В работе [45] изложен общий подход к решению прямой задачи гидротурбины. Применительно к направляющему аппарату такая задача рассмотрена в работе [46] для двухмерной модели течения жидкости, а в работах сделано ее обобщение и развитие на 3Д модель[47-49].
Другой важной проблемой, связанной с расчетом силовых характеристик гидротурбины, является рациональное определение кривизны лопастей. Дело в том, что каждая направляющая поверхность при одном и том открытии а0 обтекается с различными углами атаки. На рисунке 46 показаны расчетные углы атаки на каждой из 32 лопаток модели гидротурбины с Д1 = 460 мм по трехмерной модели.
Отсутствие осевой симметрии потока перед направляющим аппаратом является причиной того, что на каждой лопатке равнодействующая сил давления, ее величина и точка приложения, а следовательно, и гидравлический момент будут различными. Указанная особенность обтекания лопаток имеет место во всем диапазоне рабочих режимов работы турбины.
Рисунок 46 - Углы атаки в градусах на лопатках для различных а0
На рисунке 47 показаны результаты распределения расчетного коэффициента момента относительно оси поворота по лопаткам для исследуемой модели, которые согласуются с результатами эксперимента в пределах допустимой погрешности.
Рисунок 47– Коэффициент Cm0 на лопатках для различных а0
С точки зрения распределения силовых характеристик по элементам привода и величины потребного гидравлического момента (с добавлением момента трения) для определения тягового момента сервомотора их величина должна быть постоянной, а изменение от а0=0 до а0max одинаковым.
Для обеспечения надежной работы турбины значения потребного момента не должны превосходить значения располагаемого тягового момента. В противном случае требуется увеличить располагаемый тяговый момент. Если последнее вследствие какой-либо причины нежелательно, то нужно найти пути изменения моментной характеристики. Одним из путей изменения моментной характеристики лопастей является изменение формы профиля [50], другим – изменение оси поворота или относительного эксцентриситета n0, характеризующего положение лопатки относительно оси поворота в закрытом положении (рисунок 48):
(3.58)
Рисунок 48 - Основные геометрические параметры радиального направляющего аппаратахф, уф.
3.4.2 Алгоритм расчета координат фокуса профиля лопастей
Известно [51], что точка, относительно которой гидравлический момент поворота не зависит от угла атаки профиля, является его фокусом. Тогда, если за ось поворота лопасти принять координаты фокуса, распределение момента поворота по лопаткам будет равномерным и постоянным в пределах безотрывного обтекания. Этот результат был получен С.А. Чаплыгиным и сформулирован в виде следующей теоремы: силы давления жидкости, действующие на профиль, могут быть приведены к подъемной силе, приложенной в фокусе, и к паре, величина момента которой не зависит от угла атаки. Найдем координаты фокуса хф, уф. Для этого воспользуемся известной из механики формулой для момента силы
(3.59)
и уравнением момента относительно входной кромки профиля В (рисунок 49).
Рисунок 49 - Схема определения фокуса профиля
(3.60)
В уравнениях (3.58) и (3.59) X и Y – проекции подъемной силы Р профиля, которая направлена перпендикулярно скорости невозмущенного потока 
, 
– момент профиля при бесциркуляционном обтекании относительно фокуса.
Если хорда профиля l совпадает с осью ОХ, тогда (3.59) можно записать следующим образом:
(3.61)
Используя выражение момента в виде
в котором Сm – безразмерный коэффициент момента; 
– плотность жидкости. Запишем уравнение (3.60) с учетом (3.61) относительно коэффициента Сm:
Приняв 
и введя безразмерные коэффициенты подъемной силы Ср, силы Ср, силы 
, a 
, перепишем последнее уравнение относительно коэффициента Сmo: Сmo, хф, уфСm,Сx, Сy
(3.62)
В уравнении (3.62) три неизвестных Сmo, хф, уф. Остальные значения величин, входящих в формулу (3.62), определяются в процессе решения задачи обтекания профиля. Поэтому для определения координат фокуса профиля хф, уф необходимо решить три раза прямую задачу и вычислить коэффициенты Сm,Сx, Сy относительно входной кромки.
В результате будем иметь:
,
, (3.63)
.
Так как Сmo – постоянная величина, тогда (3.63) можно записать таким образом:
или 
Учитывая, что в полученном выражении неизвестными являются хф, уф, перепишем его относительно неизвестных:
Аналогично получим второе выражение (3.63):
Обозначив
,
для определения координат фокуса профиля будем иметь следующую систему уравнений: 
из которой координаты фокуса будут равны:
(3.64)
Используя данный алгоритм, для исследуемой модели реальной гидротурбины были определены координаты фокуса хф, уф профиля лопастей, которые при расчете момента поворота поверхности лопасти приняты за координаты осей поворота, расположенных на диаметре Д0. Полученные результаты, представленные на рисунке 50, подтверждают предлагаемый путь целенаправленного изменения силовых характеристик турбины и могут быть рекомендованы для практического применения.Как показывает моделирование можно варьировать исходными данными и найти вариант кривизны поверхности лопастей, которые будут наименьшим образом возмущать набегающий поток [52]. Анализ расчетных данных показывает, что имеется неравномерность нагрузки на поверхности лопастей. К сожалению, математический аппарат не всегда имеет возможность описывать поставленную задачу с точностью 3-5% [53]. Для повышения качества расчетов необходимы граничные данные или заданное поле скорости, что определяется, как обычно, из эксперимента.
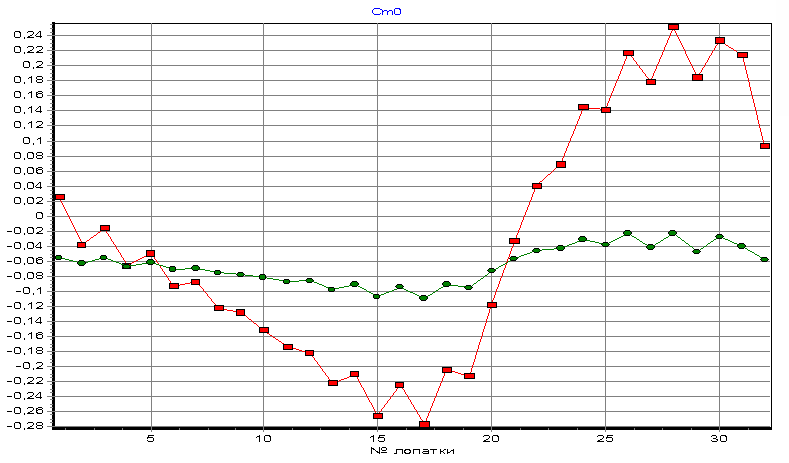
Рисунок 50– Коэффициент момента Сmo на лопастях при а0=32мм для двух вариантов оси поворота
Основной причиной неравномерного распределения сил и моментов на криволинейных поверхностях является отсутствие осевой симметрии потока перед ним.
Используя теоретический результат С.А. Чаплыгина о силе давления потока на профиль и точке ее приложения, можно целенаправленно изменять силовые характеристики турбины.
Таким образом, при симметричном течении и равномерном распределении нагрузок на лопасти турбины можно не только улучшить методику расчета, но и определить аппроксимационные линии поперечного сечения лопастей.
3.4.3 Кинематическая характеристика течения жидкости, служащая мерой завихренности течения
Циркуляция скорости(Г) - кинематическая характеристика течения жидкости или газа, которая служит мерой завихренности течения. Если скорости всех жидких частиц, расположенных на некоторой замкнутой кривой длиной l, направлены по касательной к этой кривой и имеют одну и ту же численную величину v, то циркуляция скорости определяется равенством.
Г = ul (3.65)
Такой случай имеет место для прямолинейного вихря, т. е. плоскопараллельного течения жидкости, при котором все её частицы движутся по концентрическим окружностям с центрами на оси вихря (жидкость как бы «вращается» вокруг этой оси).
Если циркуляция скорости по любому замкнутому контуру, проведённому внутри жидкости, равна нулю, то течение жидкости будет безвихревымилипотенциальным течением и потенциал скоростей будет однозначной функцией координат. Если же циркуляция скорости по некоторым контурам будет отлична от нуля, то течение жидкости будет либо вихревым в соответственных областях, либо безвихревым, но с неоднозначным потенциалом скоростей (область течения неодносвязна, т. е. в ней имеются замкнутые твёрдые границы, например быки моста в реке). В последнем случае циркуляция скорости по всем контурам, охватывающим одни и те же границы, имеет одно и то же значение. Циркуляция скорости широко используется как характеристика течений идеальной (без учёта вязкости) жидкости. Для вязкой жидкости циркуляция скорости всегда отлична от нуля и со временем изменяется вследствие диффузии вихрей.
Термин «циркуляция» был первоначально введен в гидродинамикедля расчета движения жидкости по замкнутому каналу. Рассмотрим течение идеальной несжимаемойжидкости. Выберем произвольный контур G. Мысленно представим, что мы (мгновенно) заморозили всю жидкость в объеме, за исключением тонкого канала постоянного сечения, включающего в себя контур G. Тогда, в зависимости от первоначального характера течения жидкости, она будет либо неподвижной в канале, либо двигаться вдоль контура (циркулировать). В качестве характеристики такого движения берут величину равную произведению средней скорости движения жидкости по каналу u на длину контура l.
C = ul, (3.66)
поскольку именно скорость u установится в этом случае в итоге всюду в канале, а величина циркуляции C даст (обобщенный) импульс для жидкости единичной плотности, сопряженный (обобщенной) координате, характеризующей положение жидкости как целого в канале, соответствующей, несколько упрощая, положению одиночной «пылинки» в жидкости, измеренному по линейке, изгибающейся вдоль канала.
Так как при затвердевании стенок канала нормальная к контуру компонента скорости будет погашена (вообразим, что это происходит перед тем, как тангенциальная скорость в канале всюду становится одинаковой вследствие несжимаемости жидкости), жидкость по каналу будет сразу после затвердевания двигаться с тангенциальной составляющей исходной скорости vτ. Физический смысл циркуляции или завихренности жидкости состоит в том, что вихревой поток имеет не только энергию поступательного течения среды, но и энергию вихревого движения потока. Например, для решения проблемы создания экономичной и наиболее эффективной системы создания подъёмной тяги в НТЦ "Взлёт" разработана вихревая подъёмная система. Теоретической основой для разработки вихревой пoдъемно-тяговой системы является предложенная в 1912 году Н.Е.Жукoвским вихревая теория воздушного винта. Согласно этой теории, лопасти винта заменяются системой присоединенных и свободных вихрей, образующих в общем случае винтовую вихревую пeлену.В этой работе впервые была сформулирована идея создания воздушного винта с оптимальным (равномерным) распределением индуктивной скорости (элементарных тяг) по ометаемой площади. По имени автора такой винт назван «винтом НЕЖ» или «идеальным» винтом. При этом решается обратная задача, в которой скорости на периферии вихря близки к нулю и имеют максимальную величину в его центре, что приближает форму его поперечного сечения к форме лопасти «винта НЕЖ» и создает эпюру единичных тяг (индуктивных скоростей), характерную для «запредельного» винта.
Это очень важно для гидротурбины, в котором наблюдается вихревое движение потока, которое создается за счет внутренних криволинейных лопастей турбины. Поэтому в такой конструкции необходимо учитывать циркуляцию жидкости, которая будет источником вращения лопастей турбины.
Вращательное движение твердого тела характеризуется угловой скоростью, а вращательное движение жидкой частицы - вихрем скорости (rot v). Для характеристики циркуляционных движений среды обе эти величины не конструктивны, хотя циркуляция и связана с вихрем. Для них вводится интегральная характеристика Г, определяемая по зависимости (3.65).
Интеграл берется вдоль некоторого замкнутого контура L, состоящего из фиксированных частиц. Это означает, что контур L перемещается вместе с этими частицами. Такой контур называют жидким контуром.
Найдем полную производную по времени t от контурного интеграла (3.65). Для этого перейдем к лагранжевым переменным, взяв в качестве естественного параметра кривой ее длину. Тогда удается показать, что
(3.67)
Следовательно, производная по времени от циркуляции скорости равна циркуляции ускорения. Эта величина обращается в нуль, если ускорение жидкой частицы является полным дифференциалом. Используя уравнение движения, получаем:
(3.68)
Через U обозначен потенциал сил тяжести. Поскольку подынтегральное выражение в первом интеграле (3.68) представляет собой полный дифференциал, то
(3.69)
Равенство (3.69) является следствием консервативности поля сил тяжести и центростремительных сил.
Отличие от нуля означает возможность возникновения вихревых течений жидкости. Чтобы установить возможность возникновения циркуляционных течений, рассмотрим их связь с вихревыми движениями сплошных сред.
Согласно известной теореме Стокса [54] для произвольного вектора А имеет место равенство
(3.70)
где n - нормаль к поверхности S, опирающейся на контур L, а сам контур L ограничивает односвязную область. Поэтому
(3.71)
Следовательно, циркуляция скорости - скалярная величина, имеющая смысл потока вихря через поверхность S, опирающуюся на замкнутый контур L. Это позволяет утверждать, что наличие циркуляционных течений жидкости в значительной мере связано с проблемой возникновения вихрей.
3.4.4 Расчет параметров малонапорной гидротурбины
Гидротурбина, преобразующая механическую энергию воды в энергию вращающегося вала генератора. По принципу действия конструкции гидротурбины делятся на активные и реактивные. Основным рабочим органом гидротурбины, в котором происходит преобразование энергии, является рабочее колесо. Вода подводится к рабочему колесу в активных гидротурбинах через сопла, в реактивных — через направляющий аппарат. В активной гидротурбине вода перед рабочим колесом и за ним имеет давление, равное атмосферному.
В реактивной гидротурбине давление, воды перед рабочим колесом больше атмосферного, а за ним может быть, как больше, так и меньше атмосферного давления.
Первая реактивная гидротурбина была изобретена в 1827 французским инженером Б. Фурнероном; эта гидротурбина имела на рабочем колесе мощность 6 л. с., но из-за низких энергетических свойств подобные гидротурбины уже не применяются. Основная причина низкого КПД – высокое сопротивление лопастей рабочего колеса и большие геометрические размеры. В 1855 американский инженер Дж. Френсис изобрел радиально-осевое рабочее колесо гидротурбины с неповоротными лопастями [55]. Данные конструкции работали уже при средних напорах и при изменении расхода воды наблюдались вибрация и кавитация поверхностей лопасти [56].Для улучшения режима работы гидротурбины в 1887 немецкий инженер Финк предложил направляющий аппарат с поворотными лопатками [57]. Данная конструкция позволяет приспосабливать конструкцию турбины к изменению расхода или напора воды. В 1889 американский инженер А. Пелтон разработал активную — ковшовую гидротурбину [58], которая имеет положительное давление на поверхности лопасти и устраняется ударное воздействие потока на рабочее колесо. На сегодняшний день распространенными конструкциями гидротурбин являются поворотнолопастные. Несмотря на то, что в 1920 австрийский инженер В. Каплан получил патент на поворотнолопастную гидротурбину, тем не менее, это направление широко развивается и применяется в большинстве действующих ГЭС.
Для расчета профиля лопасти рабочего колеса гидротурбины, вращающегося с постоянной угловой скоростью, используется уравнение [59]:
(3.72)
где Н — рабочий напор Гидротурбины, т. е. запас энергии 1 кг воды (разность отметок горизонтов воды перед входом в сооружения гидравлической силовой установки и по выходе из них за вычетом потерь на сопротивление во всех сооружениях, но без вычета потерь в самой Гидротурбине); U1 и U2 — окружные скорости лопастей на входе воды в рабочее колесо и на выходе из него, м/сек; V1 и V2 — абсолютные скорости воды на входе и выходе, м/сек; (α1 и α2 — углы между направлениями окружных и абсолютных скоростей в точках, соответствующих осереднѐнной по энергии поверхности тока, град; g — ускорение свободного падения, м/сек2(рисунок 51).
Рисунок 51 – Схема расчета гидротурбины
В левую часть уравнения вводится множитель 
, являющийся гидравлическим кпд гидротурбины. Часть мощности, полученная колесом, расходуется на преодоление механических сопротивлений, эти потери учитываются механический кпд гидротурбин 
. Утечка воды в обход рабочего колеса учитывается объемным кпд гидротурбины.
Полный КПД гидротурбины 
– отношение полезной мощности, отдаваемой турбинным валом, к мощности пропускаемой через гидротурбину воды. В современной гидротурбине полный кпд равен 0,85—0,92; при благоприятных условиях работы лучших образцов гидротурбина он достигает 0,94—0,95.
Геометрические размеры гидротурбины характеризуются номинальным диаметром D, рабочего колеса. Гидротурбина разных размеров образуют турбинную серию, если обладают однотипными рабочими колесами и геометрическими подобными элементами проточной части. Определив необходимые параметры одной из гидротурбины данной серии, можно подсчитать, пользуясь формулами подобия, те же параметры для любой гидравлической турбины этой серии. Каждую турбинную серию характеризует коэффициент быстроходности, численно равный частоте вращения вала гидротурбины, развивающей при напоре 1 м мощность 0,7355 кВт (1 л. с.). Чем больше этот коэффициент, тем больше частота вращения вала при заданных напоре и мощности. Гидротурбина и электрический генератор обходятся дешевле при увеличении частоты их вращения, поэтому стремятся строить гидротурбины с возможно большим коэффициентом быстроходности. Однако в реактивных гидротурбинах этому препятствует явление кавитации, вызывающее вибрацию агрегата, снижение кпд и разрушение материала гидротурбины.
Графики, выражающие зависимости величин, характеризующих гидротурбину, называются турбинными характеристиками. На рисунке 52 представлены характеристики гидротурбины при постоянном напоре и частоте вращения колеса, но при различных нагрузках и расходе воды.
h — КПД; Q — расход воды; N — нагрузка гидротурбины
Рисунок 52 – Характеристики гидротурбины при постоянном напоре и частоте вращения колеса
В реальных условиях гидротурбины работают при меняющемся напоре; их поведение в этом случае изображается универсальными характеристиками для модели и эксплуатационными характеристиками — для натурной гидротурбины универсальные характеристики строятся на основании лабораторных исследований модели, проточная часть которой геометрически подобна натурной.
Проточная часть реактивных гидротурбин состоит из следующих основных элементов (рисунок 53): спиральной камеры гидротурбины 1; направляющего аппарата 2, регулирующего расход воды; рабочего колеса 3 и отсасывающей трубы 4, отводящей воду от гидротурбины. Реактивные гидротурбины по направлению потока в рабочем колесе делятся на осевые и радиально-осевые.
Рисунок 53 – Проточная часть реактивной гидротурбины
По способу регулирования мощности реактивные гидротурбины бывают одинарного и двойного регулирования. К гидротурбинам одинарного регулирования относятся гидротурбины содержащие направляющий аппарат с поворотными лопатками, через который вода подводится к рабочему колесу (регулирование в этих гидротурбинах производится изменением угла поворота лопаток направляющего аппарата), и лопастнорегулируемые гидротурбины, у которых лопасти рабочего колеса могут поворачиваться вокруг своих осей (регулирование в этих гидротурбин производится изменением угла поворота лопастей рабочего колеса) [60]. Гидротурбина двойного регулирования содержат направляющий аппарат с поворотными лопатками и рабочее колесо с поворотными лопастями. Поворотнолопастные гидротурбины, применяемые на напоры до 150 м, могут быть осевыми и диагональными гидротурбинами. Разновидностью осевых являются двухперовые, в которых на каждом фланце размещаются по две лопасти вместо одной. Радиально-осевые гидротурбины одиночного регулирования применяют на напоры до 500—600 м. Активные гидротурбины строят преимущественно в виде ковшовых гидротурбин и применяют на напоры выше 500—600 м; их делят на парциальные и непарциальные. В парциальных гидротурбинах вода к рабочему колесу подводится в виде струй через одно или несколько сопел и поэтому одновременно работает одна или несколько лопастей рабочего колеса. В непарциальных гидротурбинах вода подводится одной кольцевой струей и поэтому одновременно работают все лопасти рабочего колеса. В активных гидротурбинах отсасывающие трубы и спиральные камеры отсутствуют, роль регулятора расхода выполняют сопловые устройства с иглами, перемещающимися внутри сопел и изменяющими площадь выходного сечения. Крупные гидротурбины снабжаются автоматическими регуляторами скорости.
По расположению вала рабочего колеса гидротурбины делятся на вертикальные, горизонтальные и наклонные [61]. Гидротурбина с гидрогенератором называют гидроагрегатом. Горизонтальные гидроагрегаты с поворотно-лопастными или пропеллерными гидротурбинами могут выполняться в виде капсульного гидроагрегата.
Основными тенденциями в развитии гидротурбины являются: увеличение единичной мощности, продвижение каждого типа гидротурбины в область повышенных напоров, совершенствование и создание новых типов гидротурбин, улучшение качества, повышение надежности и долговечности оборудования.
4 РАЗРАБОТКА ЧЕРТЕЖЕЙ И ПОДГОТОВКА ЭКСПЕРИМЕНТАЛЬНОЙ МОДЕЛИ
На основании приведенной расчетной схемы были определены геометрические параметры гидротурбины, согласно их были разработаны чертежи. При разработке чертежей особое внимание уделялось повышению пропускной способности конструкции. Для определения геометрических размеров гидротурбины необходимо на каждом сечении определять потенциал скорости, который является важным параметром при составлении чертежей (рисунок 54).
Рисунок 54 – Чертежи гидротурбины
Рисунок 55 – Общий вид гидротурбины
Разработка чертежей сопровождались экспериментальными исследованиями. Некоторые узлы корректировались не один раз. Разработанные чертежи представлены в ПриложенииБ.
5 ПОДГОТОВКА ЭКСПЕРИМЕНТАЛЬНОЙ МОДЕЛИ
Для определения правомерности использования математической модели необходимо проведение экспериментальных исследований. Чтобы исследования провести в том формате, в котором можно получить такие данные, как это было показано при расчетной схеме. Главным образом эксперименты проводятся для определения поля скорости потока и распределения давления вдоль конструкции гидротурбины. Для экспериментов создается модель гидротурбины в уменьшенном размере (рисунок 56).
Рисунок 56 – Экспериментальная модель прямоточной гидротурбины
Компоненты и узлы гидротурбины желательно сделать разъемными (рисунок 57, 58).
Рисунок 57 – Завихритель гидротурбины
Рисунок 58 – Гидроколесо гидротурбины
Изготовление гидротурбины из составных частей упрощает разработку чертежей, а также изготовление деталей конструкции (рисунок 59). Представляется возможным, не меняя основные узлы, изменять параметры, например, гидроколеса, и получать данные, оптимальные для начальных и граничных условий.
Рисунок 59 – Составные части гидротурбины
Расчетная схема позволяет определить параметры гидротурбины, по которым представляется возможным разработать чертежи гидротурбины. Каждый узел гидротурбины представляет собой уникальные части нового оборудования. Поэтому очень важно показать в чертежах соединение узлов гидротурбины, которые имеют свое конкретное назначение. Другим важным моментом является реальная возможность изготовление деталей в наших условиях. Поэтому чертежи изготавливались в упрощенном варианте, вполне доступным в изготовлении деталей и узлов гидротурбины нашими специалистами.
ЗАКЛЮЧЕНИЕ
Проведены литературный обзор, патентный поиск и теоретические исследования существующих конструкций малонапорных гидротурбин.
На основании рассмотренных уравнений механики жидкости и гидравлики разработана методика расчета вихревого движения жидкости в гидротурбине с применением теории турбулентных струй, которая позволяет производить оценку и анализ параметров течения.
Установлено, что применение вихревого эффекта в гидроагрегате расширяет возможности исполнения конструкции и повышает надежность ее работы.
Предложена методика моделирования процесса вихревого движения жидкости в гидротурбине, которая отличается от существующих тем, что для обеспечения эффективности работы гидротурбины определяются критические, технологические параметры, влияющие на вращение гидротурбины и позволяющие установить наиболее оптимальные режимы.
Основными тенденциями в развитии гидротурбины являются: увеличение единичной мощности, продвижение каждого типа гидротурбины в область повышенных напоров, совершенствование и создание новых типов гидротурбин, улучшение качества, повышение надежности и долговечности оборудования.
На основе расчетных данных разработаны предварительные рабочие чертежи для изготовления экспериментальной модели конструкции малонапорной гидротурбины. Учитывая погрешности математических расчетов при определении размеров конструкции гидротурбины необходимо предусмотреть возможность изменения начальных и граничных условий при изготовлении экспериментальной установки. Места сопряжения с подводящим и отводящим водоводами желательно сделать съемными, чтобы изучить различные виды и типы соединения турбины с водоводом. На съемных элементах также можно разместить приборы и датчики учета.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 Гидроэнергетика. Гидропотенциал. Гидроэлектростанции. https://www.ecomuseum.kz/dieret/hydro/hydro.html
2 Мартынова Н.С. Модели течения жидкости в радиальном направляющем аппарате гидротурбины и особенности их численной реализации// ВісникСумДУ, 2001.