Тема 1.Электростатика
Лекция №22.
Циркуляция вектора напряженности электростатического поля.
Потенциал электростатического поля.
Диэлектрики, поляризация.
Циркуляция вектора напряженности электростатического поля.
Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд Q0, то сила, приложенная к заряду, совершает работу.
Работа силы F на элементарном перемещении dl равна
Так как 
·cosa=dr, то
Работа при перемещении заряда Q0 из точки 1 в точку 2 будет равна
(1)
Из формулы (1) следует, что работа не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек.
Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными.
Определение 1.
Если работа поля, совершаемая действующими силами при перемещении пробного объекта из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений, то такие поля называются потенциальными, а силы, действующие в них, — консервативными.
Из формулы (1) также следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.
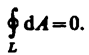(2)
Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то с учётом определения напряжённости элементарная работа сил поля на пути dl будет равна Е ·dl = El· dl, где El = E·cosa — проекция вектора Е на направление элементарного перемещения.
|
|
Тогда формулу (2) можно записать в виде
(3)
Определение 2.
Интеграл вида 
называется циркуляцией вектора напряженностиэлектростатического поля по замкнутому контуру – L.
Потенциал электростатического поля
Объект, находящейся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа.
Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу (см. формулу (1) предыдущего раздела) сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q0 в начальной и конечной точках поля заряда Q:
(1)
Из (1)следует, что потенциальная энергия заряда Q0 поле заряда Q будет равна
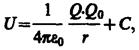(2)
где 
произвольная постоянная.
Если считать, что при удалении заряда в бесконечность (r®¥) потенциальная энергия обращается в нуль (U=0), то С=0 и потенциальная энергия заряда Q0, находящегося в поле заряда Q на расстоянии r от него, будет равна
(3)
Из формулы (3) вытекает, что отношение U/Q0 не зависит от Q0 и может служить энергетической характеристикой электростатического поля.
Определение 1 (вспомогательное!).
Потенциал j в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку,
(4)
Работа, совершаемая селами электростатического поля при перемещении заряда Q0 из точки 1 в точку 2, может быть представлена как произведение перемещаемого заряда на разность потенциалов в начальной и конечной точках.
|
|
(5)
С другой стороны, работа сил поля при перемещении заряда Q0 из точки 1 в точку 2 может быть записана также в виде
(6)
Приравняв выражения (5) и (6), придем к выражению для разности потенциалов:
(7) Если перемещать заряд Q0 из произвольной точки за пределы поля, т. е. в бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, будет равна A¥=Q0·j, откуда
(8)
Определение 2(основное!)
Потенциал — физическая величина, численно равная работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.
Единица потенциала — Вольт (В).
Определение 3.
1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл).
Определение 4.