(16.3)
Если L = const, то
. (16.4)
Электродвижущая сила самоиндукции противодействует в соответствии с правилом Ленца изменению тока в контуре, замедляя его убывание или возрастание. Мерой инертности контура по отношению к изменению в нем тока является индуктивность контура.
 |
Закон изменения силы тока в цепи (рис.16.1) при включении или отключении источника постоянного тока с ЭДС (Е) имеет вид
, (16.5)
где I 0 – сила тока в начальный момент времени (при t = 0), R – электрическое сопротивление цепи, L – ее индуктивность.
При замыкании цепи начальный ток I 0 = 0 и зависимость силы тока от времени имеет вид
. (16.6)
График этой зависимости показан на рис.16.2.
 |
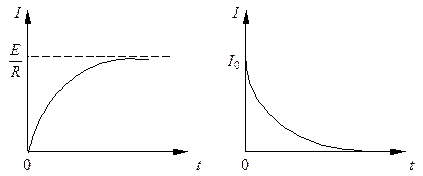Рис.16.2 Рис.16.3
При отключении источника ЭДС (без изменения сопротивления R цепи) ток в цепи убывает по закону
. (16.7)
График этой зависимости показан на рис. 16.3.
Взаимной индукцией называется явление возникновения электродвижущей силы в одном из контуров при изменении силы электрического тока в другом, индуктивно связанном с первым контуром (рис.16.4).
 |
Если в контуре 1 течет ток силой I 1, то магнитный поток, создаваемый этим током, пропорционален I 1. Обозначим ту часть потока, которая пронизывает контур 2, Ф21.
Тогда
Ф21 = L 21 I 1, (16.8)
где L 21 – коэффициент пропорциональности.
Если ток I 1 изменяется, то в контуре 2 индуктируется ЭДС Ei 2, которая, по закону Фарадея - Ленца, равна скорости изменения магнитного потока Ф21, созданного током I 1 в первом контуре и пронизывающего второй:
. (16.9)
Аналогично при протекании в контуре тока I 2 магнитный поток (его поле на рис. 16.4 изображено пунктиром) пронизывает первый контур. Если Ф12 – часть этого потока, пронизывающего контур 1, то
|
|
Ф12 = L 12 I 2. (16.10)
Если ток I 2 изменяется, то в контуре индуктируется ЭДС Ei 1, равная скорости изменения магнитного потока Ф12, созданного током I 2 во втором контуре и пронизывающего первый:
. (16.11)
Коэффициенты пропорциональности L 12 и L 21 называются взаимной индуктивностью контуров. Можно показать, что если контуры находятся в неферромагнитной среде, то L 12 = L 21 = М.
Взаимная индуктивность М зависит от геометрической формы, размеров, взаимного расположения контуров и магнитной проницаемости окружающей контуры среды.
Единица измерения взаимной индуктивности та же, что и для индуктивности – генри (Гн).
Выражение для ЭДС взаимной индукции при условии (L 12 = L 21 = М = = const):
и 
. (16.12)
Выражение для взаимной индуктивности двух соленоидов, намотанных на общий сердечник:
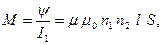(16.13)
где 
и 
- плотность витков первой и второй катушек соответственно.
Энергия магнитного поля, связанного с током в проводнике, равна
. (16.14)
Объемной плотностью энергии w m магнитного поля называется энергия этого поля, отнесенная к его объему:
, (16.15)
где dWm – энергия, заключенная в малом объеме dV поля, который выбран таким образом, чтобы в его пределах поле можно было считать однородным. В изотропной, линейной и неферромагнитной среде
, (16.16)
где В и Н – модули векторов магнитной индукции и напряженности в рассматриваемой точке поля.
Примеры решения задач
Задача 1. По соленоиду течет ток I = 2 А. Магнитный поток Фm, пронизывающий поперечное сечение соленоида, равен 4 .10-6 Вб. Определить индуктивность соленоида, если он имеет N = 800 витков.
|
|
Дано:
I = 2 А
Фm = 4 .10-6 Вб
N = 800 витков
L -?
ному со всеми N витками соленоида, когда по нему идет ток, равный единице силы тока, т.е.
,
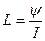где y - потокосцепление, равное
.
Тогда
.
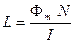Подставим численные значения и вычислим L:
= 1,6 .10-3 Гн.
Ответ: L = 1,6 .10-3 Гн.
Задача 2. Если сила тока, проходящего в некотором соленоиде, изменяется на 50 
, то на концах соленоида возникает среднее значение ЭДС самоиндукции, равное 0,08 В. Найти индуктивность соленоида.
Дано: Решение
= const 1. По закону Фарадея - Ленца
< Es > = 0,08 В 
,
L -? где y - потокосцепление.
2. Потокосцепление равно y = L I, тогда 
, так как индуктивность соленоида не изменяется.
3. Если ток в соленоиде изменяется по произвольному закону, то 
выражает среднее изменение тока в единицу времени, тогда 
выражает среднее значение < Es > за интервал времени D t.
Следовательно,
.
Вычислим значение индуктивности:
= 1,6 .10-3 Гн.
Ответ: L = 1,6 .10-3 Гн.
Задача 3. Обмотка соленоида состоит из одного слоя плотно прилегающих друг к другу витков медного провода. Диаметр провода d = 0,2 мм, диаметр соленоида D = 5 см. По соленоиду течет ток I = 1 А. Определить, какое количество электричества протечет через обмотку соленоида, если концы ее замкнуть накоротко. Толщиной изоляции пренебречь.
Дано:
d = 0,2 мм = 2 .10- 4 м
D = 5 см = 5 .10-2 м
I = 1 А
rмеди = 1,7 .10-8 Ом.м
q -?
По закону Ома
,
где R – сопротивление соленоида, а I – индукционный ток, текущий через соленоид при замыкании обмотки.
|
|
Тогда
По закону Фарадея - Ленца
Тогда
.
Интегрируя полученное выражение, получаем
где 
- начальное потокосцепление, 
- конечное.
Потокосцепление y пропорционально силе тока в соленоиде, следовательно,
, а = 0,
так как ток в этот момент обратится в нуль.
Тогда
или
Индуктивность соленоида равна
,
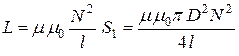где l – длина соленоида.
Сопротивление
,
где lпр – длина медного провода, S 2 – его площадь.
Длина провода
lпр = p D N,
где p D – длина одного витка, N – число витков, S 2 = 
– площадь сечения провода.
Тогда
.
Подставим индуктивность и сопротивление в формулу заряда:
.
Длина соленоида находится из соотношения
,
где d – диаметр провода, а N – число витков соленоида (витки плотно прилегают друг к другу).
Тогда
.
Подставим числа и вычислим
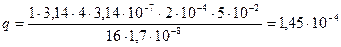Кл.
Ответ: q = 1,45 .10-4 Кл.
Задача 4. Соленоид с железным сердечником длиной 50 см и площадью сечения S = 10 см2 имеет 1000 витков. Найти индуктивность этого соленоида при токах: 1) I = 0,1 А; 2) I = 0,2 А; 3) I = 2 А.
Дано:
l = 50 см = 0,5 м
S = 10 см2 = 10-3 м2
N = 1000
1) I = 0,1 А
2) I = 0,2 А
3) I = 2 А
L -?
среда обладает свойством намагничиваться, то m ¹ 1. Железо является ферромагнетиком, оно сильно намагничивается при внесении в магнитное поле, m железа » 1. При протекании тока по соленоиду создается однородное магнитное поле, напряженность которого
.
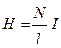Индукция магнитного поля 
,
.
Магнитная проницаемость зависит от Н, а Н – от тока I. Зависимость μ от Н представлена на рис. 16.5.
 |
Рис.16.5
Зная напряженность магнитного поля, созданного током I, можно найти индукцию магнитного поля В для данного значения напряженности, воспользовавшись графиком зависимости В от Н (см. прил.), а затем вычислить μ - магнитную проницаемость для данного тока I в соленоиде.
= 400 
.
.
.
Из графика определяем
В 1 = 0,8 Тл, В 2 = 1,2 Тл и В 3 = 1,6 Тл.
Вычислим значение 
.
Тогда
Гн.
Гн.
Гн.
Ответ: L 1 = 8 Гн, L 2 = 6 Гн, L 3 = 0,8 Гн.
Задача 5. На соленоид с немагнитным сердечником длиной 0,2 м и площадью поперечного сечения 3.10-3 м2 надет проволочный виток. Число витков соленоида N 1 = 320. Какая средняя ЭДС взаимоиндукции возникнет в витке, если ток соленоида I = 3 А выключить в течение D t = 0,001 с.
Дано:
l = 0,2 м
S = 3 .10-3 м2
N 1 = 320
N 2 = 1
I 1 = 3 А
I 2 = 0
D t = 0,001 с
< Евз > -?
4) 
5) 
, D I = I 2 – I 1 = 0 – I 1, m = 1 (сердечник немагнитный).
В.
Ответ: < Евз > = 0,018 В.
Задача 6. На один немагнитный сердечник намотаны две катушки, имеющие индуктивности L 1 = 0,2 Гн и L 2 = 0,8 Гн. Какой ток потечет во второй катушке, если ток I 1 = 0,3 А в первой катушке выключить в течение 0,001 с. Сопротивление второй катушки R 2 = 600 Ом.
Дано:
L 1 = 0,2 Гн
L 2 = 0,8 Гн
I 1 = 0,3 А
R 2 = 600 Ом
D t = 0,001 с
I 2 -?
Решая эти три уравнения, получаем
,
то есть
.
Тогда
.
Подставляя численные значения, находим
А.
Ответ: I 2 = 0,2 А.
Задача 7. На железный стержень длиной 50 см и сечением 2 см2 намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию магнитного поля в сердечнике соленоида, если сила тока в обмотке 0,5 А.
Дано:
l = 50 см = 0,5 м
S = 2 см2 = 2 .10-4 м2
= 20 
= 2.103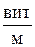 
I = 0,5 А
Wт -?
Индуктивность
,
где 
- объем соленоида, 
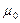- магнитная постоянная, 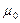= 4 p ·10-7 
.
,
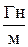где В – индукция магнитного поля внутри соленоида, Н – напряженность.
Подставив в формулу энергии индуктивность и магнитную проницаемость, получим
,
.
Найдем величину Н
Н = 2 .103 . 0,5 = 103 
.
Тогда величину В можно найти из графика зависимости В от Н (см. прил.).
При Н = 103 
В = 1,3 Тл.
Вычислим энергию магнитного поля
= 0,065 Дж.
Ответ: Wт = 0,065 Дж.
Задача 8. При индукции магнитного поля В = 1 Тл объемная плотность энергии магнитного поля в железе wт = 200 
. Какова магнитная проницаемость m железа в этих условиях?
Дано:
В = 1 Тл
wт = 200 
m -?
Из второй формулы можно определить m непосредственно:
Вычислим m:
.
Ответ: m = 2000.
Задача 9. При некоторой силе тока плотность энергии магнитного поля соленоида (без сердечника) w = 0,2 . Во сколько раз увеличится плотность энергии поля при той же силе тока, если соленоид будет иметь железный сердечник?
Дано:
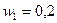
I 1 = I 2
H 1 = I 1 n, H 2 = I 2 n, I 1 = I 2, H 1 = H 2;
. (2)
При одном и том же токе напряженность поля будет одна и та же.
(нет сердечника).
Тогда
.
Из формулы (1) следует
.
Из графика зависимости В от Н (см. приложение) находим
В 2 = 1 Тл, В 2 = 
Н.
Тогда
;
.
Ответ: .
Задача 10. Катушка имеет сопротивление R = 10 Ом и индуктивность L = 0,144 Гн. Через сколько времени после выключения в катушке возникнет ток, равный половине установившегося?
Дано:
R = 10 Ом
L = 0,144 Гн
t -?
,
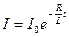где I 0 – установившийся ток в катушке (начальный ток), I – ток в момент времени t, R – сопротивление катушки, L – ее индуктивность.
Тогда
;
с.
Ответ: t » 9 .10-3 с.