Задание на лабораторную работу.

Министерство общего и профессионального образования РФ.

Иркутский государственный технический университет.

Математическое программирование

(Часть 1 Методы безусловной оптимизации)

 

Методические указания к лабораторным работам для студентов специальности 2201

(Четвертый семестр обучения).

 

Иркутск 1998 г.

Математическое программирование. Часть 1. “Методы безусловной оптимизации”. Методические указания по выполнению лабораторных работ. Составил доцент кафедры вычислительной техники Хрусталев Ю. П. - Иркутск, 1998 г - с - 18.

Рассмотрены методы решения задач математического программирования: нахождение безусловного экстремума градиентными методами и методом наискорейшего спуска.

Приведены различные алгоритмы нахождения безусловных экстремумов квадратичных функций. Сформулированы условия, необходимые для существования стационарных точек функций многих переменных.

Даны варианты заданий на лабораторные работы и рассмотрены примеры выполнения работ.

Библиография - 3 назв. Табл. - 4.

 

Содержание:

 

		Стр.
	Аннотация.
	Нахождение безусловного экстремума функции двух переменных градиентными методами.
	Метод наискорейшего спуска.
	Литература.

 

Лабораторная работа №1.

“Нахождение безусловного экстремума функции нескольких переменных градиентными методами”.

 

Цель работы: знакомство с градиентными методами нахождения безусловного экстремума.

Работа выполняется с использованием алгоритмических языков высокого уровня.

На работу отводится 6 часов.

 

Одной из важнейших задач анализа является задача отыскания экстремума (наибольшего или наименьшего значения) скалярной функции f (x), n - мерного векторного аргумента x при некоторых ограничениях. Эту задачу будем записывать следующим образом:

 

(1)

(2)

 

Здесь X - некоторое подмножество евклидового пространства E_n. Будем называть X допустимым множеством задачи (1) - (2), а точки, принадлежащие X, - ее допустимыми точками [1].

Задачу максимизации функции f (x) также можно записать в виде (1) - (2), заменив f (x) на .

Точка x^*ÎX доставляет глобальный минимум функции f (x) на множестве X, если при некотором достаточно малом e>0 для всех X не равных x*, x Î X и удовлетворяющих условию.

выполнено неравенство

Если допустимое множество X составляет n - мерное пространство (X = E_n), то имеет место задача безусловной минимизации функции нескольких переменных.

Будем предполагать, что f (x) имеет в окрестности исследуемой точки непрерывные первую и вторую производные. Тогда имеет место теорема 1:

Для того, чтобы в точке функция имела безусловный локальный экстремум, необходимо, чтобы все ее частные производные обращались в в нуль.

 

(3)

 

Вес точки , удовлетворяющее условию называются стационарными.

Условие стационарности (3) записывают также в виде

 

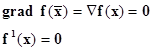(4)

 

n - мерный вектор с константами - градиент функции f (x) в точке .

Так как предполагается, что функция f (x) дважды непрерывно дифференцируема по всем переменным, то существует матрица ее вторых производных - матрица Гессе.

 

 

Выражение вида:

 

(6)

 

называется квадратичной формой.

Имеет место следующая теорема [1] (теорема 2):

Для того, чтобы дважды непрерывно дифференцируемая функция n переменных f (x) имела в стационарной точке безусловный локальный минимум (максимум), необходимо, чтобы матрица ее вторых производных была неотрицательно (неположительно) определенной и достаточно, чтобы она была положительно (отрицательно) определенной.

Если X - вектор размерности n, а A - квадратная симметричная матрица порядка n x n, то квадратичная форма имеет вид .

Если все главные миноры матрицы A положительны,

т. е. то матрица A и соответствующая ей квадратичная форма называется положительно определенными.

Алгоритмы численных методов отыскания безусловного экстремума функции n переменных основаны на использовании приведенных выше теорем. При этом находится последовательность векторов {X_k}, при которых

 

Такая последовательность называется релаксационной, а методы ее построения - методами спуска.

В зависимости от максимального порядка производных минимизируемых функций, вычисление которых предполагается, алгоритмы безусловной минимизации делятся на классы:

* методы нулевого порядка (методы поиска) - используют значение самой функции;

* методы первого порядка требуют кроме того вычисления первых производных минимизируемой функции и т.д.

Градиентные методы являются методами первого порядка.

Градиент скалярной функции f (x) в некоторой точке x_k направлен в сторону наискорейшего возрастания функции.

Антиградиент - вектор, противоположный градиенту , направлен в сторону наискорейшего убывания функции.

Выбрав в качестве направления спуска в точке X^k антиградиент, получим итерационный процесс.

 

(6)

 

Итерационные процессы, в которых направление движения на каждом шаге совпадает с градиентом (антиградиентом), называются градиентными методами.

Градиентные методы отличаются выбором шага a:

* методы с постоянным шагом;

* методы с дроблением шага.

Удобнее при поиске экстремума использовать не антиградиент - а нормированный антиградиент[2]

 

 

где

 

В этом случае формула (5) примет вид

 

(7),

 

где

От выбора a существенно зависит скорость сходимости алгоритма поиска экстремума. При больших a процесс сходится быстрее, однако вблизи экстремальной точки возможны колебания (либо процесс может вообще расходиться).

В методе с дроблением шага указанный недостаток отсутствует. В этом методе a_k выбирается таким образом, чтобы выполнялось неравенство:

 

(8)

 

где 0<e<1

Если на какой - то итерации условие (8) выполняется, переходим к следующей итерации. В противном случае дробим шаг a_k (делим пополам) до тех пор, пока условие (8) не будет выполнено.

Итерационный процесс (7) заканчивается, при выполнении условия где e₁ - заданная точность вычислений (в точке экстремума градиент равен нулю).

 

Задание на лабораторную работу.

Найти безусловный экстремум функции двух переменных с заданной точностью e₁:

* градиентным методом с постоянным шагом для двух различных значений a_k;

* градиентным методом с дроблением шага при заданном e.

Начальные значения: X₁=10; X₂= - 10.

Результаты вычислений свести в таблицы вида:

 

а) Таблица 1,1: Итерационный процесс нахождения безусловного экстремума градиентным методом с постоянным шагом a=a₁, a_2.

 

Итерация

 

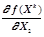
б) Таблица 1,2. Итерационный процесс нахождения безусловного экстремума градиентным методом с дроблением шага.

 

N ите-рации	N ша-га

 

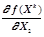
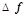
Итерационный процесс поиска экстремума с постоянным шагом прекратить, если число итераций превышает 100.

 

Варианты заданий.

 

N
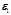
			0,8		0,5	0,001
			0,7		0,6	0,001
			0,6		0,7	0,001
N
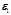
			0,5		0,8	0,001
			0,4		0,9	0,001
			0,3		0,5	0,001
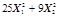
			0,2		0,6	0,001
			0,1		0,7	0,001
			0,8		0,8	0,001
			0,7		0,9	0,001
			0,6		0,5	0,005
			0,5		0,6	0,005
			0,4		0,7	0,005
			0,3		0,8	0,005
			0,2		0,9	0,005
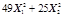
			0,1		0,5	0,005
			0,8		0,6	0,005
			0,7		0,7	0,005
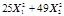
			0,6		0,8	0,005
			0,5		0,9	0,005
			0,8		0,5	0,001
			0,7		0,6	0,001
			0,6		0,7	0,001
			0,5		0,8	0,001
			0,8		0,8	0,001