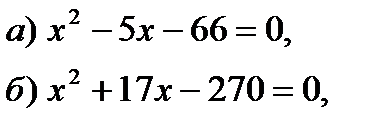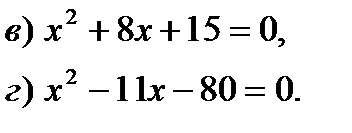Свойство 1. Если в уравнении ах2 + bх +с = 0, а + b + с = 0, то один из его корней равен 1, а другой, в соответствии с теоремой Виета, равен с/а.
Доказательство: Имеем а+b+с=0, тогда b= - (а+с). Найдем дискриминант D=b2 -4ас= а2+2ас+с2 - 4ас = а2- 2ас+с2=(а - с)2. Формула корней этого квадратного уравнения имеет вид: 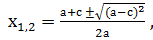
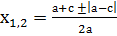 . Отсюда имеем
. Отсюда имеем 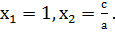 Что и требовалось доказать.
Что и требовалось доказать.
Пример 1: х2 + х – 2 = 0; а = 1, в = 1, с = -2. Так как 1+1–2 =0, то х1 =1, х2 = -2.
Свойство 2. Если в уравнении ах2 + bх + с = 0, а – b + с = 0 или b=a+c, то один из его корней равен –1, а другой –с/а.
Доказательство: Имеем а - b+с=0, тогда b= а+с. Найдем дискриминант D=b2 -4ас= а2+2ас+с2 - 4ас = а2- 2ас+с2=(а - с)2. Формула корней этого квадратного уравнения имеет вид: 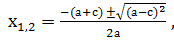
 . Отсюда имеем
. Отсюда имеем 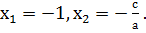 Что и требовалось доказать.
Что и требовалось доказать.
Пример 2: х2 – х – 2 = 0. Так как 1 – (- 1) + (-2) = 0, то х1 = -1, х2 = 2.
Свойство 3. Если a = c, b = a2 + 1, то x1 = - a, x2 = -1/a.
Доказательство: Имеем a = c, b = a2 + 1. Найдем дискриминант D=b2 -4ас= а4+2а2+1 - 4а2 = а4- 2а2+1=(а2 - 1)2. Формула корней этого квадратного уравнения имеет вид: 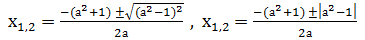 . Отсюда имеем
. Отсюда имеем 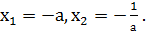 Что и требовалось доказать.
Что и требовалось доказать.
Пример 3. 3х2+10х+3=0, а=3, b=10, с=3. Так как а=с=3, b=32+1=10, то х1= -3, х2=-1/3.
Свойство 4. Если a = c, b = -(a2 + 1), то x1 = a, x2 = 1/a.
Доказательство: Имеем a = c, b = -(a2 + 1). Найдем дискриминант D=b2 -4ас= а4+2а2+1 - 4а2 = а4- 2а2+1=(а2 - 1)2. Формула корней этого квадратного уравнения имеет вид:  . Отсюда имеем
. Отсюда имеем 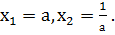 Что и требовалось доказать.
Что и требовалось доказать.
Пример 4. 3х2 - 10х+3=0, а=3,b=-10,с=3. Так как а=с=3, b=-(32+1)=-10, то х1=3, х2=1/3.
Приём переброски.
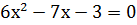 , первый коэффициент в качестве множителя «перебрасываем к -3», получим уравнение
, первый коэффициент в качестве множителя «перебрасываем к -3», получим уравнение 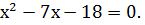
Корни 9 и -2. Делим числа 9 и (-2) на 6:


 2. Пользуясь теоремой, обратной теореме Виета, составьте квадратное уравнение, корни которого равны 2 и 5.
2. Пользуясь теоремой, обратной теореме Виета, составьте квадратное уравнение, корни которого равны 2 и 5.
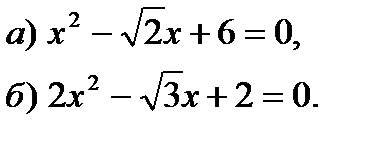 2. Пользуясь теоремой, обратной теореме Виета, составьте квадратное уравнение, корни которого равны
2. Пользуясь теоремой, обратной теореме Виета, составьте квадратное уравнение, корни которого равны  и
и  .
.