Структурный анализ механизма
На рис. 1. представлена схема исследуемого кулачкового механизма, где 0 – стойка, 1 – кулачок, 2 – коромысловый толкатель, 3- ролик.
Звенья данного кулачкового механизма образуют три кинематические пары пятого класса и одну четвертого класса. Рассчитаем число степеней свободы механизма по формуле Чебышева для плоских механизмов:
где n – количество подвижных звеньев, 
– количество кинематических пар 5-го и 4-го класса соответственно.
Формальный расчет показывает, что должно быть два входных (ведущих) звена. Фактически у этого механизма одно входное звено - кулачок 1. Ролик не изменяет закона движения выходного звена - толкателя 2. Он нужен для повышения надежности (износостойкости) механизма путем замены трения скольжения между толкателем и кулачком трением качения.
Звенья эквивалентного кулачкового механизма образуют две кинематические пары пятого класса и одну четвертого класса. Рассчитаем число степеней свободы механизма по формуле Чебышева для плоских механизмов:
где n – количество подвижных звеньев, – количество кинематических пар 5-го и 4-го класса соответственно.
Пассивным звеном является ролик.
Механизм имеет четыре фазы работы: удаление, дальний выстой, возврат и ближний выстой
Кинематический анализ механизма
Кинематический анализ производится экспериментально-аналитически. Функцию S(
) положения толкателя 2 в зависимости от угла поворота кулачка 1 получаем экспериментально в виде таблицы с шагом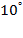 
по углу поворота кулачка. Результаты эксперимента представлены в табл. 2.1:
Таблица 2.1
| I |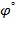 
| Ѱ˚ | i |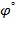
| Ѱ˚ | i |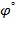
| Ѱ˚ | ||
Полагая, что кулачок вращается с постоянной скоростью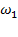 
= 10 
, следовательно, 
, получим функцию положения от времени ѱ(t).
Для этого вычислим шаг таблицы по времени:
= 
.
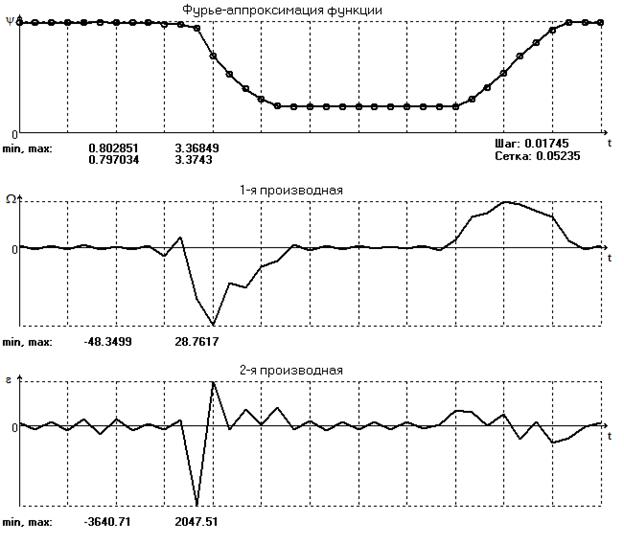
Для аналитической обработки функции ѱ(t) проведем графическое дифференцирование графика ѱ(t) из чего получим график угловой скорости ω(t) и углового ускорения ε(t).
Аппроксимация тригонометрическим рядом Фурье
Для аналитической обработки функции S(t) проведем аппроксимацию её таблицы тригонометрическим рядом Фурье. В результате этого мы получим следующие возможности:
1) Восстанавливать значения функции S(t) для любых значений аргумента
2) Дифференцированием ряда определять зависимость скорости v(t) и ускорения a(t) ползуна
Разложение функции в тригонометрический ряд Фурье означает приближенную замену тригонометрическим полиномом вида:
Где 
, 
– коэффициенты ряда, 
– частоты, по которым производится разложение, 
c – время полного оборота кривошипа 
– амплитуда сигнала на j-й частоте, 
- фаза сигнала на j-й частоте, n- число членов ряда
Формулы для вычисления коэффициента Фурье при табличном задании функции:
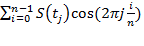
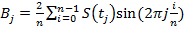
Перед выполнением операций необходимо решить вопрос о достаточном числе членов ряда m. Поскольку в данном случае функция S(t) задана таблицей значений в конечном числе точек n = 36, то максимальное число членов ряда
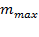= n/2 = 36/2 = 18.
i t, c Ψ, рад Ψф, рад ω, рад/с ε, рад/с^2
0 0.000e+00 3.351e+00 3.345e+00 1.301e+00 1.703e+02
1 1.745e-02 3.351e+00 3.357e+00 -1.267e+00 -1.954e+02
2 3.490e-02 3.351e+00 3.345e+00 1.394e+00 2.105e+02
3 5.235e-02 3.351e+00 3.357e+00 -1.669e+00 -2.325e+02
4 6.980e-02 3.351e+00 3.345e+00 2.325e+00 3.237e+02
5 8.725e-02 3.368e+00 3.374e+00 -1.527e+00 -4.031e+02
6 1.047e-01 3.351e+00 3.345e+00 7.769e-01 3.343e+02
7 1.222e-01 3.351e+00 3.357e+00 -1.549e+00 -2.452e+02
8 1.396e-01 3.351e+00 3.345e+00 1.687e+00 1.183e+02
9 1.570e-01 3.316e+00 3.322e+00 -5.732e+00 -1.802e+02
10 1.745e-01 3.316e+00 3.310e+00 6.741e+00 3.056e+02
11 1.920e-01 3.194e+00 3.200e+00 -3.253e+01 -3.641e+03
12 2.094e-01 2.339e+00 2.333e+00 -4.835e+01 2.048e+03
13 2.268e-01 1.780e+00 1.786e+00 -2.227e+01 -1.827e+02
14 2.443e-01 1.344e+00 1.338e+00 -2.537e+01 7.808e+02
15 2.617e-01 1.030e+00 1.036e+00 -1.202e+01 7.035e+01
16 2.792e-01 8.378e-01 8.319e-01 -8.451e+00 8.590e+02
17 2.967e-01 8.029e-01 8.087e-01 2.246e+00 -1.802e+02
18 3.141e-01 8.029e-01 7.970e-01 -1.978e+00 2.281e+02
19 3.316e-01 8.029e-01 8.087e-01 1.668e+00 -2.197e+02
20 3.490e-01 8.029e-01 7.970e-01 -1.432e+00 2.118e+02
21 3.664e-01 8.029e-01 8.087e-01 1.257e+00 -2.056e+02
22 3.839e-01 8.029e-01 7.970e-01 -1.133e+00 1.999e+02
23 4.013e-01 8.029e-01 8.087e-01 1.063e+00 -1.928e+02
24 4.188e-01 8.029e-01 7.970e-01 -1.072e+00 1.810e+02
25 4.363e-01 8.029e-01 8.087e-01 1.240e+00 -1.530e+02
26 4.537e-01 8.029e-01 7.970e-01 -1.883e+00 5.237e+01
27 4.712e-01 8.029e-01 8.087e-01 5.145e+00 7.180e+02
28 4.886e-01 1.030e+00 1.024e+00 1.933e+01 6.181e+02
29 5.060e-01 1.396e+00 1.402e+00 2.191e+01 -1.373e+01
30 5.235e-01 1.833e+00 1.827e+00 2.876e+01 5.377e+02
31 5.410e-01 2.339e+00 2.345e+00 2.671e+01 -6.278e+02
32 5.584e-01 2.758e+00 2.752e+00 2.288e+01 2.080e+02
33 5.758e-01 3.142e+00 3.147e+00 1.907e+01 -8.195e+02
34 5.933e-01 3.351e+00 3.345e+00 4.473e+00 -5.987e+02
35 6.108e-01 3.351e+00 3.357e+00 -1.744e+00 -8.456e+01
36 6.282e-01 3.351e+00 3.345e+00 1.301e+00 1.703e+02
Оценим значимость членов ряда с помощью амплитудного спектра
i Част.,1/c Част., гц Ci Фазы i
0 0.000e+00 0.000e+00 2.093e+00
1 1.000e+01 1.592e+00 1.560e+00 0.9428
2 2.000e+01 3.184e+00 3.034e-02 0.9986
3 3.001e+01 4.776e+00 3.733e-01 -0.2996
4 4.001e+01 6.367e+00 3.180e-02 0.4367
5 5.001e+01 7.959e+00 1.073e-01 -1.4673
6 6.001e+01 9.551e+00 3.796e-02 -0.2319
7 7.001e+01 1.114e+01 2.552e-02 1.2474
8 8.002e+01 1.273e+01 3.389e-02 -1.0062
9 9.002e+01 1.433e+01 2.347e-02 0.9025
10 1.000e+02 1.592e+01 2.358e-02 1.4060
11 1.100e+02 1.751e+01 2.168e-02 -0.4444
12 1.200e+02 1.910e+01 1.932e-02 1.0221
13 1.300e+02 2.069e+01 1.432e-02 -1.5004
14 1.400e+02 2.229e+01 1.725e-02 0.4860
15 1.500e+02 2.388e+01 8.408e-03 1.0737
16 1.600e+02 2.547e+01 1.248e-02 -0.5430
17 1.700e+02 2.706e+01 1.238e-02 0.3981
18 1.800e+02 2.865e+01 1.164e-02 -1.5708
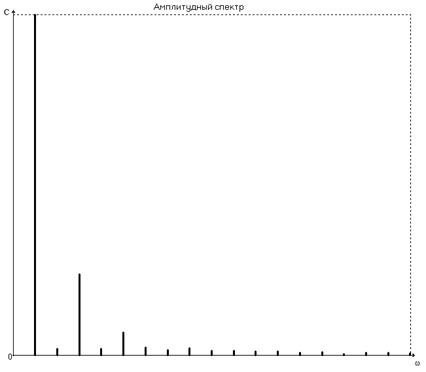
Анализ амплитудного спектра исследуемой функции показывает, что основными частотами, присутствующими в сигнале (кроме 
/2) являются вторая и четвертая 
и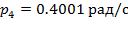 
. Предположим, что именно эти частоты несут информацию о перемещении толкателя, а на остальных частотах содержится информация лишь о «шуме» и проведем разложение в ряд и аппроксимацию функции с учетом только этих двух частот.
i t, c Ψ Ряд Произв-я 1 Произв-я 2
0 0.000e+00 3.351e+00 3.454e+00 -7.099e-01 -2.368e+02
1 1.745e-02 3.351e+00 3.412e+00 -3.682e+00 -9.994e+01
2 3.490e-02 3.351e+00 3.340e+00 -4.171e+00 4.135e+01
3 5.235e-02 3.351e+00 3.280e+00 -2.444e+00 1.475e+02
4 6.980e-02 3.351e+00 3.262e+00 5.730e-01 1.847e+02
5 8.725e-02 3.368e+00 3.299e+00 3.496e+00 1.358e+02
6 1.047e-01 3.351e+00 3.375e+00 4.847e+00 7.928e+00
7 1.222e-01 3.351e+00 3.452e+00 3.501e+00 -1.659e+02
8 1.396e-01 3.351e+00 3.479e+00 -9.170e-01 -3.350e+02
9 1.570e-01 3.316e+00 3.406e+00 -7.840e+00 -4.446e+02
10 1.745e-01 3.316e+00 3.199e+00 -1.584e+01 -4.541e+02
11 1.920e-01 3.194e+00 2.858e+00 -2.302e+01 -3.507e+02
12 2.094e-01 2.339e+00 2.411e+00 -2.754e+01 -1.554e+02
13 2.268e-01 1.780e+00 1.919e+00 -2.820e+01 8.182e+01
14 2.443e-01 1.344e+00 1.451e+00 -2.481e+01 2.976e+02
15 2.617e-01 1.030e+00 1.071e+00 -1.828e+01 4.348e+02
16 2.792e-01 8.378e-01 8.216e-01 -1.030e+01 4.603e+02
17 2.967e-01 8.029e-01 7.089e-01 -2.860e+00 3.754e+02
18 3.141e-01 8.029e-01 7.087e-01 2.359e+00 2.142e+02
19 3.316e-01 8.029e-01 7.731e-01 4.488e+00 3.133e+01
20 3.490e-01 8.029e-01 8.480e-01 3.664e+00 -1.156e+02
21 3.664e-01 8.029e-01 8.897e-01 9.144e-01 -1.843e+02
22 3.839e-01 8.029e-01 8.777e-01 -2.217e+00 -1.593e+02
23 4.013e-01 8.029e-01 8.192e-01 -4.176e+00 -5.433e+01
24 4.188e-01 8.029e-01 7.453e-01 -3.856e+00 9.468e+01
25 4.363e-01 8.029e-01 7.002e-01 -8.817e-01 2.421e+02
26 4.537e-01 8.029e-01 7.278e-01 4.342e+00 3.466e+02
27 4.712e-01 8.029e-01 8.590e-01 1.080e+01 3.811e+02
28 4.886e-01 1.030e+00 1.104e+00 1.719e+01 3.381e+02
29 5.060e-01 1.396e+00 1.451e+00 2.221e+01 2.282e+02
30 5.235e-01 1.833e+00 1.866e+00 2.490e+01 7.548e+01
31 5.410e-01 2.339e+00 2.303e+00 2.478e+01 -8.939e+01
32 5.584e-01 2.758e+00 2.714e+00 2.190e+01 -2.350e+02
33 5.758e-01 3.142e+00 3.055e+00 1.684e+01 -3.345e+02
34 5.933e-01 3.351e+00 3.295e+00 1.060e+01 -3.698e+02
35 6.108e-01 3.351e+00 3.425e+00 4.352e+00 -3.344e+02
36 6.282e-01 3.351e+00 3.454e+00 -7.099e-01 -2.368e+02
3. Выводы по работе:
1. Тригонометрические ряды Фурье целесообразно применять для аппроксимации гладких периодических функций.
2. Если необходимо, чтобы значения ряда в узлах совпадали со значениями аппроксимируемой функции, то следует производить разложение с максимально возможным числом членов ряда.
3. Ряд Фурье позволяет сглаживать функции, искаженные, например, погрешностями эксперимента. Для такой сглаживающей аппроксимации следует при разложении учитывать лишь первые основные частоты, что в первом приближении определяется по амплитудному спектру, но в общем случае является отдельной, не всегда простой, задачей.
4. Необходимо иметь ввиду, что та математическая обработка функции, которая применялась в данной работе ни коим образом не может устранить влияние погрешностей эксперимента