Цель работы
1.1 Приобретение умений определения расчетным путем и оформления результатов прямых и косвенных измерений
Методическое обеспечение
2.1 Методические указания по выполнению лабораторной работы
Последовательность выполнения работы
3.1 Изучить методические указания по выполнению лабораторной работы
3.2 Выполнить задание по расчету погрешностей прямых и косвенных измерений согласно варианта
Теоретическое обоснование
Обработка прямых измерений
Одно значение измеряемой величины (отдельный результат прямого измерения), получаемое в процессе измерительного эксперимента, называется наблюдением. Окончательный результат измерения в общем случае находят, выполняя обработку нескольких наблюдений.
Процедура обработки заключается в общем случае в выполнении нескольких операций: исключение из ряда полученных наблюдений явно ошибочных, определение числового значения (оценки) собственно результата измерения (для косвенных измерений — по функциональной зависимости искомой величины от исходных), проведение статистической обработки, нахождение показателей точности измерения (оценки погрешности), выбор формы представления окончательного результата. При однократных (одиночных) прямых измерениях результат измерения совпадает с наблюдением.
Запись окончательного (обработанного) результата любого измерения должна содержать численное значение результата и оценку суммарной погрешности. Например, корректная запись результата измерения сопротивления R может выглядеть так: R = 106,2 Ом; ∆ = ±2,5 Ом.
Погрешность результата следует записывать одной или двумя значащими цифрами, причем вес младшего значащего разряда в числе результата измерения должен совпадать с весом младшего значащего разряда в числе погрешности. Скажем, неправильно записывать окончательный результат измерения напряжения таким образом: U= 224,6 В; ∆ = ±5 В;
|
|
Различают однократные (одиночные) и многократные (множественные) прямые измерения.
Однократные измерения - это самые простые по выполнению и обработке - наиболее распространены в практике технических измерений - и означают получение окончательного результата по одному разовому наблюдению (отсчету).
Пример
Цифровой вольтметр обеспечивает измерение постоянного напряжения в пределах 0..1000В с пределами измерения: 1В; 10В; 100В; 1000В. Предельное значение основной относительной погрешности определяется выражением
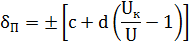
где c=0,15; d=0,02 – коэффициенты;
Uк – конечное значение выбранного диапазона измерения, В;
U – значение измерительного напряжения, В.
Определить величину предельного значения основной абсолютной погрешности на возможных пределах измерения при измерении напряжения U=9 В. Какой предел измерения следует выбрать для получения более точного результата?
Решение
1 Измерить напряжение U=9 В заданным цифровым вольтметром возможно на пределах измерения Uк1=10 В; Uк2=100 В; Uк3=1000 В.
2 Определим предельные значения основных относительных погрешностей на вышеуказанных пределах измерения
3 Определим предельные значения основной абсолютной погрешности на указанных пределах измерения
|
|
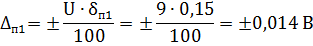
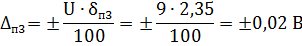
4 Результаты измерения напряжения цифровым вольтметром на указанных пределах измерения могут быть представлены в форме
U1 = (9±0,014) В
U2 = (9±0,032) В
U3 = (9±0,02) В
Следовательно, наиболее точный результат будет получен на приделе измерений U1 = 10В.
Обработка косвенных измерений
Косвенные измерения в практике электрических измерений встречаются довольно часто. Вопрос оценки погрешности результата измерения - один из важнейших в таких экспериментах. Имея подробную исходную информацию о применяемых средствах измерения, измеряемых величинах и условиях проведения эксперимента, можно достаточно строго решить задачу оценки суммарной погрешности результата измерения. Правда, требуется четко оговаривать все допущения. Возможны два подхода к решению этой задачи: детерминированный и вероятностный, рассмотрим первый подход.
Детерминированный подход (иногда называемый методом наихудшего случая) более характерен для обычных технических измерений и экспресс-измерений с их обычно упрощенными моделями процессов и подходами. Перед рассмотрением этого подхода оговорим необходимые допущения:
- инструменты исправны, имеют реальные погрешности, соответствующие своим классам точности. Причем их погрешности - только систематические, т.е. не меняющиеся в течение данного эксперимента. Случайных погрешностей нет;
- исходные измеряемые величины характеризуются неизменными (в течение данного эксперимента) значениями основных параметров;
- условия работы СИ - нормальные или рабочие;
- функциональная зависимость искомой величины Y от исходных величин Xi известна достаточно точно;
|
|
- оператор имеет достаточную квалификацию.
Если интересующая нас величина /связана с исходными величинами Xj известной функциональной зависимостью F
Y = F(X1,X2,…Xn) (1)
и предельные значения абсолютных погрешностей А,- определения каждой исходной величины Х{ известны, то предельное значение абсолютной погрешности Дг результата измерения искомой величины У в общем случае можно определить по так называемой формуле накопления частных погрешностей
∆Y =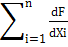 
∆I, (2)
где 
- частные производные функционала F no каждой исходной
величине в точках, соответствующих найденным значениям величин Xi;
∆i - предельные значения абсолютных погрешностей определения
исходных величин Xj.
Рассмотрим два частных, но довольно распространенных, случая функциональной зависимости F.
Первый частный случай - функционал F имеет вид суммы. Если функциональная зависимость имеет вид
Y = 
(3)
где α - коэффициенты функциональной зависимости, то предельное значение абсолютной погрешности ∆Y определяется по формуле
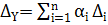(4)
Относительная погрешность δУ, %, при этом может быть найдена обычным образом
δY = 
(5)
Например, если Y= 5Х1 + 2Х2 + Х3, то ∆Y= 5∆1 + 2∆2 + ∆з.
Второй частный случай - функционал F имеет вид произведения. Если функциональная зависимость имеет вид
Y = 
(6)
где П - знак произведения я сомножителей;
αi - коэффициенты - показатели степени исходных величин Xh, то
предельное значение относительной погрешности δY определяется по формуле
δY =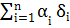 
(7)
где δi,- предельные значения относительных погрешностей определения исходных величин Xt.
Предельное значение абсолютной погрешности A Y затем находится обычным образом
∆Y = 
(8)
Например, если функционал Y имеет вид
Y = 
(9)
то значение относительной погрешности
δУ=2δ1 + 3δ2 + 5δ3 (10)
И хотя формально третье слагаемое должно входить в сумму со знаком минус, но, поскольку предельные значения отдельных погрешностей практически всегда симметричны (±), то в худшем случае (самое неблагоприятное сочетание значений и знаков всех составляющих) предел общей погрешности есть сумма модулей отдельных составляющих.
Пример
Определить предел допустимой абсолютной погрешности величины при ее косвенном измерении, если известна ее функциональная зависимость. Происходит измерение активной мощности P цепи постоянного тока с помощью амперметра и омметра. Класс точности амперметра на пределах измерения 0…20 мА и 0…200 мА задан в виде 0,4/0,1; класс точности омметра с пределами 0…1 Ом и 0…10 Ом задан в виде 0,2/0,4. Значение измеренных величин: сила тока I=120 мА, сопротивление R=1,3 Ом. Функциональная зависимость P=I2·R.
Решение
1 По значению измеренных величин определяем, что измерение силы тока амперметром происходило в диапазоне 0…200 мА с Ik=200 мА, измерение сопротивления омметром происходило на диапазоне 0…100 Ом с Rk=100 Ом.
2 Определим предельные значения основных относительных погрешностей амперметра и омметра.
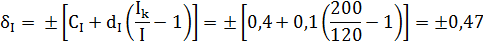
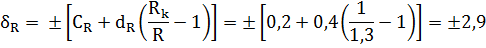
3 С учетом функциональной зависимости измеряемых величин косвенного метода измерением определим сумму предельных относительных погрешностей с учетом вклада в функцию их составляющих
4 Определим абсолютную погрешность косвенного определения активной мощности
5 Результат косвенного измерения может быть оформлен в виде
Индивидуальное задание
5.1 Цифровой вольтметр обеспечивает измерение постоянного напряжения до 1000 В. На пределах измерений 1, 10, 100, 1000 В пределы допускаемых значений погрешности измерения, выраженные в процентах, равны
,
где δ – относительная погрешность, %;
c,d – коэффициенты;
Uk – конечное значение выбранного предела измерения, В;
U – значение измеряемого напряжения, В.
Исходные данные согласно варианта приведены в таблице 1.
Необходимо:
- сформулировать определение «класса точности» средств измерений;
- объяснить физический смысл коэффициентов «c» и «d»;
- рассчитать величину предела допускаемой основной абсолютной погрешности на каждом пределе измерения;
- проанализировать полученные результаты и установить предел измерения прибора, на котором измерения будут проводиться с наименьшей погрешностью.
Таблица 1 – Исходные данные
| № варианта | с | d | U, В |
| 0,2 | 0,08 | ||
| 0,5 | 0,06 | ||
| 0,4 | 0,07 | ||
| 0,6 | 0,09 | ||
| 0,25 | 0,04 | ||
| 0,15 | 0,02 | ||
| 0,5 | 0,08 | ||
| 0,2 | 0,06 | ||
| 0,3 | 0,07 | ||
| 0,2 | 0,04 | ||
| 0,4 | 0,05 | ||
| 0,35 | 0,06 | ||
| 0,45 | 0,03 | ||
| 0,5 | 0,04 | ||
| 0,45 | 0,05 |
5.2 Определить пределы допускаемой абсолютной погрешности величины при ее косвенном измерении, если известна функциональная зависимость между искомой величиной и величинами, значения которых найдены с помощью цифровых приборов путем прямых измерений. Исходные данные приведены в таблице 2.
Необходимо:
- сформулировать определение косвенного метода измерения;
- составить формулу накопления частных погрешностей для заданной функциональной зависимости;
- определить пределы допускаемой абсолютной погрешности величины при ее косвенном измерении, если известна функциональная зависимость между измеряемой величиной и величинами, которые найдены с помощью цифровых приборов путем прямых измерений;
- проанализировать полученные результаты косвенного метода измерения.
Таблица 2 – Исходные данные
| Вариант | Искомая величина | Функциональная зависимость | Класс точности | U | I | R2 | R3 | R4 | ||
| вольтметра на пределах 10; 100 В | амперметра на пределах 20; 200 mА | омметра на пределах 1; 100 Ом | В | mА | Ом | Ом | Ом | |||
| R, Ом | R = U / I | 0,2 / 0,1 | 0,5 / 0,1 | - | - | - | - | |||
| R, Ом | R = U / I | 0,1 / 0,05 | 0,4 / 0,2 | - | - | - | - | |||
| U, В | U = I · R4 | - | 0,7 / 0,1 | 0,4 / 0,08 | - | - | - | 3,3 | ||
| U, В | U = I · R4 | - | 0,9 / 0,2 | 0,3 / 0,1 | - | - | - | 1,8 | ||
| I, mА | I = U / R3 | 1,5 / 0,5 | - | 0,6 / 0,2 | - | - | 9,1 | - | ||
| I, mА | I = U / R3 | 1,5 / 0,1 | - | 0,7 / 0,1 | - | - | 0,8 | - | ||
| R, Ом | R1 = R2 · R3 / R4 | - | - | 0,8 / 0,1 | - | - | 0,2 | 5,6 | ||
| R, Ом | R1 = R2 · R3 / R4 | - | - | 0,7 / 0,4 | - | - | 2,7 | 0,3 | 3,3 | |
| Р, Вт | Р = I2 · R3 | - | 0,4 / 0,1 | 0,2 / 0,4 | - | - | 1,3 | - | ||
| Р, Вт | Р = I2 · R3 | - | 0,6 / 0,1 | 0,8 / 0,2 | - | - | 2,7 | - | ||
| U, В | U = I · R2 | - | 0,7 / 0,1 | 0,4 / 0,08 | - | 3,3 | - | - | ||
| U, В | U = I · R2 | - | 0,8 / 0,4 | 0,3 / 0,2 | - | 1,8 | - | - | ||
| I, mА | U = I / R2 | 1,5 / 0,1 | - | 0,7 / 0,1 | - | 0,8 | - | - | ||
| R, Ом | R1 = R2 · R3 / R4 | - | - | 0,5 / 0,1 | - | - | 2,7 | 0,3 | 3,3 | |
| Р, Вт | Р = I2 · R4 | - | 0,5 / 0,2 | 0,7 / 0,1 | - | - | - | 2,7 |
6 Содержание отчета (отчет по практической работе выполняется на листах формата А4)
6.1 Цель работы
6.2 Результаты обработки измерений, выполненные в виде решения задач 6.1 и 6.2 согласно варианта
Список литературы
1 Панфилов, В. А. Электрические измерения: учебник / В. А. Панфилов. – Москва: Издательский центр «Академия», 2004. – 492 с.
2 Шишмарёв, В. Ю. Электрорадиоизмерения: учебник / В. Ю. Шишмарёв, В. И. Шанин. – Москва: Издательский центр «Академия», 2004. – 398 с.
3 Электрические измерения (с лабораторными работами): учебник /
Р. М. Демидова [и др.]. – Москва: Энергоиздат, 1983. – 392 с.