Решение двух обыкновенных дифференциальных уравнений
В этом разделе рассмотрены два дифференциальных уравнения, решения которых будут неоднократно использоваться в курсе. Это уравнение релаксационного типа, описывающее, например, движение частицы в вязкой сплошной среде. И уравнение динамики осциллятора под действием внешней силы.
Уравнение релаксационного типа
Уравнение часто встречается в различных физических приложениях и описывает динамику системы в диссипативной среде. В качестве примера рассмотрим движение твердой частицы в вязком газе. Скорость частицы 
определяется силой трения, которая в линейном приближении зависит от разности скорости газа 
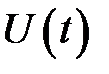и частицы
, 
.
Здесь 
– начальная скорость частицы, 
– время динамической релаксации.
Решение уравнения ищем в виде суммы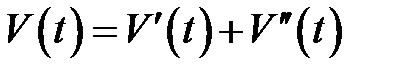 
, состоящей из общего решения однородного уравнения с заданным начальным условием 
и частного решения неоднородного уравнения 
с нулевым начальным условием. Решение однородного уравнения имеет вид
, 
, 
.
Частное решение неоднородного уравнения ищем методом вариации постоянной 
. В результате подстановки в уравнение находим уравнение для коэффициента 
с нулевым начальным условием
, 
.
Решение последнего уравнения очевидно
.
Окончательно решение уравнения релаксационного типа записывается в виде
.
Решение описывает затухание начальной скорости в результате диссипации и вовлечение частицы в движение несущей среды. Для постоянной скорости среды 
решение принимает простую форму
.
Из формулы видно, что для времен 
скорость частицы стремится к скорости несущей среды. Начальная информация в диссипативной среде забывается за время порядка времени динамической релаксации. На рис. 1 представлено изменение скорости частицы во времени, рассчитанное по формуле. Видно, что уменьшение времени релаксации приводит к сокращению периода выхода скорости частицы на стационарный уровень.
Для периодического воздействия на систему 
формула принимает вид
Рис. 1. Скорость частицы в диссипативной среде.
Вычисление интеграла реализуется следующим образом
Скорость частицы в среде с периодическими флуктуациями скорости равна
.
Видно, что при больших временах 
скорость частицы также принимает колебательный характер, однако амплитуда скорости существенно снижается с ростом времени динамической релаксации.
Рис. 2. Скорость частицы в вязкой осциллирующей среде.
Рисунок 2 иллюстрирует выход инерционной частицы на стационарный режим колебаний в вязкой среде. Видно, что рост времени релаксации приводит к меньшей амплитуде колебаний и увеличению периода выхода на стационарный режим.
Осциллятор. Явление резонанса
Уравнение и начальные условия для амплитуды колебаний осциллятора под действием возмущения имеют вид
,
, 
.
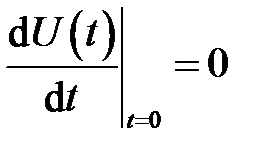Решение уравнения ищем в виде суммы 
общего решения однородного уравнения 
и частного решения неоднородного уравнения 
с заданными начальными условиями. Общее решение однородного уравнения имеет вид
.
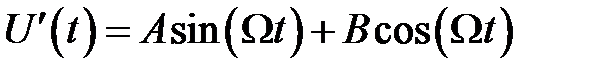Решение неоднородного уравнения ищем методом вариации постоянной
.
Рассчитываем производные
.
Далее полагаем
.
Из формул и видно, что удовлетворить нулевым начальным условиям можно потребовав выполнения условий 
.
Расчет второй производной от функции с учетом равенства приводит к выражению
Подстановка формул и в уравнение приводит к выражению
.
Система уравнений и служит для расчета производных от функций 
и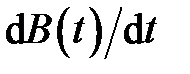 
, 
.
Решение этих уравнений с нулевыми начальными условиями имеет вид
, 
.
Подставив эти выражения в формулу, получаем
.
Решение однородного уравнения при начальных условиях тождественно равно нулю. Таким обратом, решение задачи - имеет вид
.
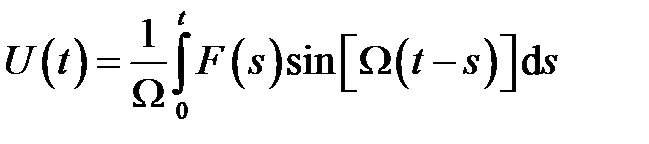Для периодического внешнего воздействия 
вычисление интеграла в формуле приводит к следующему выражению
.
Из формулы видно, что при совпадающих частотах внешней силы и осциллятора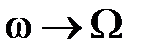 
существует неопределенность типа 
. Раскрывая эту неопределенность по правилу Лопиталя, находим
.
Совпадение частот приводит к резонансу, когда амплитуда растет линейно со временем.
Рис. 3. Иллюстрация резонанса.
Из рис. 3 видно, что при несовпадающих частотах наблюдаются биения, совпадение частот приводит к росту амплитуды колебаний.