Санкт-Петербургский Государственный Университет Телекоммуникаций им. проф. М.А. Бонч-Бруевича
Кафедра ПРЭС
Курсовой проект по дисциплине
“Прикладная механика”
Работу выполнил:
Ст. Гр. ТСС-71
Игорев А.Н.
Руководитель проекта:
Чуракова Л.Д.
Санкт-Петербург
Содержание:
1. Определение равнодействующей плоской системы сил
2. Определение центра тяжести фигуры
3. Расчёт на прочность элемента конструкции РЭА
4. Расчет задачи
Список литературы
Определение равнодействующей плоской системы сил
Вариант № 15
Условие задачи:
Блок радиоаппаратуры находится под действием системы 3 сил, заданных модулями 
сил, величинами углов 
, составленных силами с положительной осью X, и координатами 
и 
точек приложения сил. Требуется определить равнодействующую силу. Исходные значения указаны в таблице 1.
Таблица 1.
Значение сил, углов и координат.
| Силы, Н | Углы, град | Координаты, см | ||||||
| 
| 
| 
| 
| 
| x1/ y1 | x2/ y2 | x3/ y3 |
| 45/ –35 | 15/ 45 | –35/ 15 |
Решение:
1)Определение главного вектора аналитически
Fx = F * cosα; 
Fy = F * sinα;
cos 165= cos (120 + 45)= cos120 * cos45 – sin120 * sin45 = – 
* 
– 
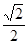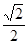* = –0,97;
cos120 = – = – 0,5;
cos 240 = – = – 0,5;
sin 165 = sin (120 + 45) = sin120 * cos45 + cos120* sin45 = * 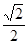– * 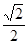= 0,26;
sin 120 = = 0,87;
sin 240 = – = – 0,87.
Определяем проекции сил , , на координатные оси X,Y:
F1x = F1 * cos165 = 75 * (– 0,97) = – 72,75 Н;
F1y = F1 * sin165 = 75 * 0,26 = 19,5 Н;
F2x = F2 * cos120= 85 * (– 0,5) = – 42,5 Н; (1)
F2y = F2 * sin120 = 85 * 0,87 = 73,95 Н;
F3x = F3 * cos240 = 110 * (– 0,5) = – 55 Н;
F3y = F3 * sin240 = 110 * (– 0,87) = – 95,7 Н;
Определяем проекции главного вектора системы на оси координат:
Rx =Σ Fix = – 72,75 – 42,5 – 55 = –170,25; (2)
Ry =Σ Fiy = 19,5 + 73,95 – 95,7 = – 2,25;
Расчёты по формулам (1) и (2) приводятся в таблице 2, в которой также определили главный момент системы:
Таблица 2.
| Номер силы, i | Значение силы Fi, Н | Угол направления силы, град | Координаты, м | Проекции сил, Н | Проекции сил, Н | Произведения величин, Н/м | Главный момент системы Mo,Н/м | ||
| Xi | Yi | Fix | Fiy | Xi*Fiy | Yi*Fix | ––– | |||
| 0,45 | –0,35 | –72,75 | 19,5 | 8,775 | 25,46 | ––– | |||
| 0,15 | 0,45 | – 42,5 | 73,95 | 11,025 | –19,13 | ––– | |||
| –0,35 | 0,15 | – 55 | – 95,7 | 33,495 | – 8,25 | ––– | |||
| Суммарное значение параметра | –170,25 | – 2,25 | 53,3 | – 1,9 |
Определяем главный вектор системы:
H
Где значения 
и 
принимают из таблицы. Направление главного вектора определяет угол 
, который определяем из формул:
Определение главного момента системы сил относительно начала координат:
2)Определение главного вектора системы сил графически.
Построение выполнили на листе формата А3. Масштабы длин и сил выбраны так, чтобы максимально использовать площадь листа. Определим масштабные значения величин:
где l, F –действительное значение длины и силы соответственно,
-масштабный коэффициент длин,
- масштабный коэффициент сил.
Учитывая заданные значения координат, наносят на чертеже координатные оси, точки приложения сил 1,2,3, и изображаем сами силы.
Определяем действительное значение главного вектора
Где масштабное значение 
мм, принимают по чертежу.
Направление вектора определяем по чертежу:
=181 градус.
3)Относительные отклонения определения параметров графическим способом.
Отклонения не превышают 2-3%, следовательно, построения и расчёты выполнены правильно.
4)Определение значения и положения равнодействующей.
Определяем плечо пары сил:
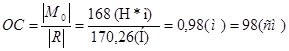
Где С - точка приложения равнодействующей.
- действительные значения главного момента и главного вектора, определённые аналитически.
Определение центра тяжести фигуры
Условия:
Определить координаты центра тяжести (центра масс) шасси блока РЭА. Шасси изготовлено из листового материала и представляет собой сложную фигуру.
a=280 мм; b=140 мм; c=65мм.
Решение:
При аналитическом определении положения центра тяжести (центра масс) исходят из понятия “центр параллельных сил”. Полагая, что материал тела сплошной и однородный, приведём формулы для определения координат центра тяжести (центра масс) сложной фигуры:
Где 
- площадь i–ой части сложной фигуры.
–координаты центра тяжести i–ой части фигуры.
n – число частей сложной фигуры.
Вычисление координат центра тяжести (центра масс) простых фигур составляющих сложную:
1)
2)
3)
4)
Вычисление координат центра тяжести (центра масс) сложной фигуры:
Координаты центра тяжести фигуры [93,84; 58,74; 8,72] мм (относительно начала координат).