ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Вариант 21
1. При производстве детали вероятность брака равна 0,2. За день изготавливаются две детали. Составить закон распределения случайной величины – количества изготовленных бракованных деталей. Найти числовые характеристики этой случайной величины. Какова вероятность того, что будет изготовлено не более одной бракованной детали?
2. Независимые случайные дискретные величины X, Y заданы законами распределения.
| X | ||||
| P | 0,2 | 0,1 | 0,4 | p |
| Y | -1 | |
| P | 4/5 | 1/5 |
Найти: 1) р; 2) функцию распределения случайной величины X и построить ее график;
3) математическое ожидание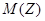 
и дисперсию 
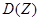случайной величины Z=X-5Y.
Вариант 22
1. В городе два коммерческих банка. У каждого риск банкротства в течение года составляет 15%. Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года. Найдите числовые характеристики. Чему равна вероятность того, что в течение года обанкротятся не более одного банка?
2. Независимые случайные дискретные величины X, Y заданы законами распределения.
| X | -2 | |||
| P | 0,2 | 0,4 | 0,1 | p |
| Y | ||
| P | 0,5 | 0,5 |
Найти: 1) р; 2) функцию распределения случайной величины X и построить ее график; 3) математическое ожидание 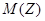и дисперсию 
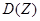случайной величины Z=5X-Y.
Индивидуальное задание № 4
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Вариант 23
1. База снабжает два магазина. В течение дня от каждого из них с вероятностью 1/4 может поступить заявка. Построить ряд распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа заявок, поступивших на базу за день. Найтивероятность того, что их будет не менее одной.
2. Независимые случайные дискретные величины X, Y заданы законами распределения.
| X | -1 | |||
| P | 0,2 | 0,1 | 0,2 | p |
| Y | ||
| P | 3/5 | 2/5 |
Найти: 1) р; 2) функцию распределения случайной величины X и построить ее график;
3) математическое ожидание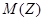 
и дисперсию 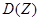случайной величины Z=4X-Y.
Вариант 24
1. Хорошим считается руководитель, принимающий 75% правильных решений. Такому управляющему банком предстоит принять решения по двум важным вопросам банковской политики. Составьте ряд распределения возможного числа правильных решений управляющего и найдите числовые характеристики. Чему равна вероятность того, что управляющий примет менее двух правильных решений?
2. Независимые случайные дискретные величины X, Y заданы законами распределения.
| X | ||||
| P | 0,2 | p | 0,3 | 0,1 |
| Y | ||
| P | 1/4 | 3/4 |
Найти: 1) р; 2) функцию распределения случайной величины X и построить ее график;
3) математическое ожидание 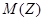и дисперсию 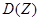случайной величины Z=X-4Y.
Индивидуальное задание № 4
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Вариант 25
1. При передаче сообщения вероятность искажения одного знака 0,15. Передано сообщение из трех знаков. Случайная величина Х - число "искажений". Найти ряд распределения и числовые характеристики этой случайной величины. Чему равна вероятность того, что в сообщении будет не более одного искажения?
2. Независимые случайные дискретные величины X, Y заданы законами распределения.
| X | -2 | |||
| P | 1/6 | p | 1/5 | 1/3 |
| Y | ||
| P | 0,7 | 0,3 |
Найти: 1) р; 2) функцию распределения случайной величины X и построить ее график;
3) математическое ожидание 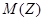и дисперсию 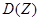случайной величины Z=2X+3Y.
Вариант 26
1. В библиотеке есть только техническая и математическая литература. Вероятность взять техническую книгу - 0,7. Случайная величина Х- число читателей, если всего читателей три, взявших математическую книгу. Найти ряд распределения и числовые характеристики этой случайной величины. Чему равна вероятность того, что читателей, взявших математическую книгу, будет не более двух?
2. Независимые случайные дискретные величины X, Y заданы законами распределения.
| X | ||||
| P | 0,1 | p | 0,2 | 0,4 |
| Y | -1 | |
| P | 1/3 | 2/3 |
Найти: 1) р; 2) функцию распределения случайной величины X и построить ее график;
3) математическое ожидание 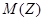и дисперсию 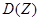случайной величины Z=2X+Y.