Порядок выполнения работы

ЛАБОРАТОРНАЯ РАБОТА 15

ИЗУЧЕНИЕ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛ

И ОПРЕДЕЛЕНИЕ СИЛЫСОПРОТИВЛЕНИЯ ГРУНТА

НА МОДЕЛИ КОПРА

 

В лабораторной работе на основе опытных данных определяются кинематические, динамические и энергетические характеристики тел при поступательном движении.

 

Описание работы установки

Для забивания свай в грунт применяется копер, который состоит из двух вертикальных направляющих брусьев, вдоль которых может двигаться тяжелый груз. Падая на сваю с некоторой высоты, груз забивает ее в грунт.

Вертикальный разрез модели копра (по осевой плоскости) показан на рис. 1.1. Груз 4 может перемещаться по направляющим 1 и удерживаться на заданной высоте с помощью затвора 2, установленного на зажиме 3, который закрепляется на направляющих винтом 13. Координаты нижней грани груза определяются по линейке 5. Свая 6 может перемещаться между двумя половинами 7 и 12 разрезной втулки. Груз 10, подвешенный к большому плечу рычага 9, стремится повернуть рычаг вокруг оси 8. Вследствие этого нажимной кулачок 11, которым оканчивается малое плечо рычага, оказывает давление на подвижную половину 7 разрезной втулки. В результате этого между сваей и втулкой возникает сила трения, которая моделирует силу сопротивления грунта. Передвигая груз 10 по большому плечу рычага, можно моделировать силы сопротивления разных грунтов.

 

Рис.1.1

 

Рис. 1.2

 

«Рабочий ход» груза копра состоит из трех процессов: 1 – падение груза на сваю (рис. 1.2,а); 2 – удар груза о сваю (рис. 1.2,б); 3 – погружение груза и сваи до полной остановки (рис. 1.2,в).

В начале падения нижняя грань груза имеет координату (рис.1. 2), во время удара – в начале совместного движения груза и сваи – координату , в конце совместного движения – координату . Координаты , , регистрируются с помощью линейки 5.

Таким образом установка позволяет измерить высоту падения груза , равную разности координат и :

и глубину погружения груза совместно со сваей в «грунт» , равную разности координат и :

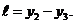
На основе определенных таким образом величин и и заданных значений масс груза и сваи можно определить кинематические, динамические и энергетические характеристики поступательного движения груза и совместного движения груза со сваей.

Порядок выполнения работы

1. Установить груз 10 на выбранном расстоянии от оси рычага 9 (модель грунта № 1). Значение записать в таблицу результатов измерений (табл. 1.1).

2. Освободив винт 13, поднять и закрепить зажим 3 на рекомендованной высоте.

3. Поднять груз и закрепить с помощью затвора в зажиме 3.

4. Определить значение координаты нижнего основания груза по линейке 5.

5. Слегка приподняв конец рычага 9 выдвинуть сваю на рекомендованную высоту.

6. Придерживая груз 4 рукой, груз освободить от зажима 3 и поставить на сваю.

7. Определить значение координаты нижнего основания груза по линейке.

8. Поднять груз 4 и закрепить в затворе 2.

9. Освободить груз 4 из затвора 2.

10. После падения груза и удара его о сваю определить координату нижней грани груза y₃ по линейке.

 

 

11. Повторить измерение при тех же значениях , , (п.п. 3 … 10) еще 2 раза.

12. Повторить измерение при двух других значениях , , (модели № 2 и № 3).

 

 

Таблица 1.1

 

 

Номер модели грунта	, м	, м	, м	, м	, м	, м	, Н
Среднее значение
Среднее значение
Среднее значение

 

Задания

(для одной из моделей грунта результаты вычислений внести в таблицу 1.2)

 

1. Вычислить среднее значение координаты нижней грани груза в конце погружения в «грунт» сваи совместно с грузом:

.

2. Выразить через координаты и высоту падения груза и вычислить .

3. Выразить через координаты и и вычислить глубину погружения сваи .

4. Принимая падение груза свободным, выразить через и вычислить:

а) время падения , используя формулу пути при равноускоренном движении;

б) скорость груза в конце падения , используя формулу скорости при равноускоренном движении;

5. Используя формулу определения импульса тела:

а) выразить через и и вычислить импульс груза в конце падения на сваю .

б) определить импульс сваи до удара груза .

 

6. а) Принимая удар груза о сваю абсолютно неупругим, т.е. принимая скорости движения груза и сваи в конце удара (в начале погружения сваи) одинаковыми и равными ,

б) пренебрегая движением груза со сваей и действием силы тяжести груза во время удара,

в) учитывая, что время взаимодействия груза и сваи во время удара одинаково,

г) используя формулы 3-го закона Ньютона и 2-го закона Ньютона, выраженного через импульсы груза и сваи и импульс силы, получить выражение скорости совместного движения груза и сваи в начале погружения через , , :

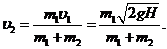(1.1)

7. Вычислить скорость совместного движения груза со сваей в начале погружения .

8. Выразить через , , и вычислить:

а) импульс груза после удара ;

б) импульс сваи после удара ;

в) изменение импульса груза при ударе ;

г) изменение импульса сваи при ударе ;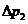

д) импульс силы удара .

9. Используя формулу, выражающую связь скорости движения с пройденным путем и ускорением, получить выражение ускорения совместного движения груза и сваи через , , , :

.

10. Вычислить ускорение при погружении сваи с грузом в «грунт».

11. Используя формулу скорости при равноускоренном движении, определить время погружения сваи с грузом в «грунт» .

12. Применяя 2-й закон Ньютона для совместного движения груза и сваи, получить выражение силы сопротивления (силы трения скольжения между сваей и разрезной втулкой) через , , , :

. (1.2)

 

13. Вычислить силу сопротивления .

14. Принимая коэффициент трения сваи об втулку равным 0,2 и используя формулу силы трения, определить силу , с которой разрезная втулка прижимает сваю.

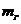15. По формуле силы тяжести определить силу тяжести груза 10 (масса груза = 0,5 кг).

16. Определить плечо силы тяжести груза , используя величину - расстояния от оси вращения рычага 9 до груза 10 (толщина груза 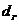= 1,5 см);

17. Определить плечо силы сопротивления , используя условие равновесия рычага 9.

18. Используя определение импульса системы тел, выразить через , , и вычислить импульс системы, состоящей из груза и сваи:

 

а) в начале удара груза о сваю ;

б) в конце удара груза о сваю .

19. Принимая удар груза о сваю за абсолютно неупругий, и применяя закон сохранения импульса, получить для скорости совместного движения груза и сваи выражение (1.1).

20. Принять за нулевой уровень отсчета потенциальной энергии высоту .

21. Используя определение механической энергии системы тел и формулы потенциальной и кинетической энергии, выразить через высоту падения груза на сваю, массу груза , массу сваи и глубину погружения сваи и вычислить механическую энергию системы, состоящей из груза и сваи:

а) в начале падения груза ;

б) в конце падения – в начале удара груза о сваю , пренебрегая потерей механической энергии на преодоление сопротивления воздуха; убедиться в справедливости закона сохранения механической энергии.

Таблица 1.2

 

Номер задания

4а

4б

5а

Величина

Наименование единицы измерения

Численное значение

 

Таблица 1.2 (продолжение)

 

5б

8а

8б

8в

8г

8д

 

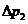
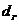
Таблица 1.2 (окончание)

 

18а

18б

21а

21б

24а

24б

∆ W 23

∆ W 23/

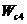
∆ W 34

 

22. Используя определение, получить выражение механической энергии системы в конце удара (в начале погружения сваи в грунт) через , , , :

 

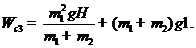
23. Вычислить энергию .

24. Выразить через , , , и вычислить:

а) потерю механической энергии системы при ударе груза о сваю ∆ W ₂₃ = - ;

б) долю потерянной механической энергии системы при ударе груза о сваю (эффективность работы копра) ∆ W ₂₃/ , учитывая

25. Определить механическую энергию системы в конце погружения сваи .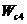

26. Выразить через , , , и вычислить изменение (потерю) механической энергии системы при погружении сваи ∆ W ₃₄.

27. Используя формулу, выражающую работу неконсервативных сил через изменение механической энергии системы, выразить работу неконсервативной силы трения скольжения сваи – силы сопротивления грунта через ∆ W ₃₄ и определить .

28. Используя выражение работы , через ∆ W ₃₄ выразить через , , , .

29. Используя формулу определения работы силы, выразить работу через силу сопротивления и глубину погружения .

30. Приравняв полученные в заданиях 28 и 29 выражения работы силы сопротивления вывести формулу силы сопротивления (1.2).

31. Принимая за полезную работу модели копра , а за затраченную работу первоначальную энергию , выразить через и и вычислить к.п.д. модели копра (долю механической энергии / , которая идет на забивание сваи), учитывая

 

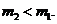
Студент ____________________________________________________

(институт, курс, группа, фамилия, и.о.)

лабораторную работу выполнил ________________________________

(подпись преподавателя)

задания к лабораторной работе выполнил ________________________

(подпись преподавателя)