Методические указания для выполнения лабораторной работы

Лабораторная работа 10

Задача о замене оборудования

Тема: Применение метода динамического программирования к решению задачи о замене оборудования в среде Excel.

Задание. В начале планового периода, продолжительностью N = 6 лет имеется оборудование возраста лет. В таблице заданы значения:

t – возраст оборудования на начало года;

r(t) – стоимость продукции, производимой за год на единице оборудования возраста t лет, t= 0,1,…T;

u(t) – расходы, связанные с эксплуата­цией этого оборудования в течение года;

s(t) – остаточная стоимость оборудования возраста t лет;

р – покупная цена нового оборудования.

Сформировать по матрице максимальных прибылей оптимальные стратегии замены оборудования начального возраста и лет для планового периода продолжительностью соответственно N и N ₁ лет. Найти максимально возможную прибыль для обеих ситуаций и прибыль за каждый год для одной из ситуаций.

Варианты

1.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

2.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

3.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

4.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

5.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

6.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

7.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

8.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

9.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

10.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

11.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

12.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

13.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

14.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

15.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

16.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

17.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

18.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

19.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

20.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

21.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

22.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

23.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

24.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

25.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

26.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

27.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

28.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

29.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

30.

t

N

t0

N1

t0

p

r(t)

u(t)

s(t)

 

Методические указания для выполнения лабораторной работы

В таблице 1 заданы значения:

t – возраст оборудования на начало года;

r(t) – стоимость продукции, производимой за год на единице оборудования возраста t лет, t= 0,1,…T;

u(t) – расходы, связанные с эксплуата­цией этого оборудования в течение года;

s(t) – остаточная стоимость оборудования возраста t лет;

р – покупная цена нового оборудования;

N – продолжитель­ность планового периода;

k = 1,2,…, N – номер года планового периода.

Сформировать по матрице максимальных прибылей оптимальные стратегии замены оборудования начального возраста и лет для планового периода продолжительностью соответственно N и N ₁ лет. Найти максимально возможную прибыль для обеих ситуаций и прибыль за каждый год для одной из ситуаций.

Таб.1

t
r(t)
u(t)
s(t)
P=20	N=5	t0=2	N1=4	t1=5	-	-	-

 

Для решения задачи применим принцип оптимальности Р.Беллмана.

Обозначим через максимальную прибыль, полученную от эксплуатации оборудования возраста t лет за последние N-k+ 1 лет планового периода. Т.е. 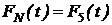– максимальная прибыль за последний год, – максимальная прибыль за последние два года, если весь плановый период составляет пять лет.

Для нахождения оптимальной политики замен следует проанализировать, согласно принципу оптимальности, процесс от конца к началу. Для этого сделаем предположение о состоянии оборудования на начало последнего года (k=N).Пусть оборудование в начале последнего года периода имеет возраст t лет. Возникают две возможности:

1) сохранить оборудование, тогда прибыль за последний год составит r(t)–u(t),

2) продать оборудование по оста­точной стоимости и купить новое, тогда прибыль за последний год будет равна s(t) – p + r (0) – u (0), где r (0) – стоимость продукции, выпущен­ной на новом оборудовании за первый год его ввода, u (0) – эксплуата­ционные расходы в этом году. Учитывая значение прибыли при различном образе действия (замена – сохране­ние), приходим к выводу, что решение о замене оборудования возраста t лет следует принять в случае, когда прибыль от нового оборудования на последнем периоде больше, чем от старого, т.е. при условии

s(t) – p + r (0) – u (0) > r(t) – u(t).

Если же s(t) – p + r (0) – u (0) ≤ r(t) – u(t), то старое оборудование целесообразно сохранить.

Следовательно, решение принимаем следующим образом (1)

Итак, для последнего года оптимальная политика и максимальная прибыль находятся из условия

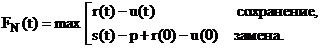(2)

Рассмотрим прибыль за два последних года. Пусть в начале предпоследнего года возрастоборудования равен t лет.Если в начале этого года принять решение о со­хранении оборудования, то к концу года будет получена прибыль . К началу последнего года возраст оборудования будет равен (t + 1) лет, и, при оптимальной политике в последнем году, оно принесет прибыль, равную . Таким образом, общая прибыль за последние два года составит . Если же в начале предпоследнего года будет принято решение о замене оборудования, то прибыль за предпо­следний год составит s(t) – p + r (0) – u (0). Поскольку приобретено но­вое оборудование, в начале последнего года его возраст будет равен одному году (t =1). Следовательно, общая прибыль за последние два года при оптимальной политике в последнем году составит .

Условно оптимальной в последние два года будет политика, доставляющая максимальную прибыль

Аналогично находим выражения для условно-оптимальной прибыли за три последних года, четыре и т.д. Общее функциональное уравнение примет вид

(3)

 

Введем исходные данные в таблицу Excel. (Рис.1)

Рис.1

Во все уравнения Беллмана (1) и (2) входят выражения и , поэтому их целесообразно вычислить, чтобы не подсчитывать для каждого значения k.

· Выделяем ячейки B7:H7.

· Печатаем знак равенства.

· Выделяем ячейки B5:H5.

· Печатаем знак минус.

· Выделяем ячейки В6:H6.

· Нажимаем Shift+Ctrl+Enter.

Для вычисления выражения выполняем следующие действия.

· Ставим курсор в ячейку B11.

· Печатаем знак равенства и, выделяя нужные ячейки, печатаем формулу

B9 – $B$10 + $B$7. Вячейке B9 находится значение , которое должноменяться, поэтому знак доллара ставить не нужно. Значения в ячейках B10 и B7 не меняются при изменении t, поэтому нужно поставить знак абсолютной ссылки. Т.е. нажать клавишу F4 после того, как нужная ячейка отобразится в формуле.

· Для заполнения ячеек C11-H11 используем операцию автозаполнения.

Сфокусируем курсор мыши на маркере автозаполнения ячейки В11. (Рис.2)

Рис.2

 

 

· Нажмем левую кнопку мыши на маркере автозаполнения и, удерживая её нажатой, переместим курсор в ячейку H11. После чего левую кнопку мыши следует отпустить. Результат последних операций отображен на рисунке 3.

Рис.3

 

Подготовим форму для вычисления значений (Рис.4)

Рис.4

 

По формуле (2) 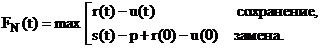необходимо вычислить значение , оно запишется в следующем виде:

· Ставим курсор в ячейку B18.

· Запускаем Мастер функций (значок или на верхней панели).

· Выбираем Другие функции.

· В окне Категория выбираем Статистические.

· В окне Функция выбираем МАКС.

· Нажимаем OK.

· В окне МАКС указываем адреса сравниваемых ячеек. (Рис.5)

· Нажимаем ОК.

 

Рис.5

 

 

· С помощью процедуры Автозаполнение заполняем ячейки C18-H18.

Вычислим

Чтобы использовать затем процедуру Автозаполнение, посмотрим какие значения в формуле

меняются с изменением t, а какие остаются неизменными. Для не изменяющихся значений нужно использовать абсолютные ссылки, т.е. с помощью клавиши F4 расставлять знак доллара.

Итак, вычисляем значение .

· Ставим курсор в ячейку B17.

· Запускаем Мастер функций (значок или на верхней панели).

· Выбираем Другие функции.

· В окне Категория выбираем Статистические.

· В окне Функция выбираем МАКС.

· Нажимаем OK.

· В окне МАКС указываем адреса сравниваемых ячеек. (Рис.6)

· Нажимаем ОК.

 

Рис.6

 

· Далее, используя функцию Автозаполнение, необходимо заполнить ячейки С17: H17.

Аналогично, используя формулу (3) последовательно заполняем ячейки B16–Н14. После выполнения вышеописанных операций получим следующую таблицу. (Рис.7)

Рис.7

 

 

Полученное решение позволяет найти максимальную прибыль за период в пять лет при первоначальном возрасте оборудования t лет. Например, если первоначальный возраст оборудования составлял 3 года, то при соблюдении оптимальной политики сохранения и замены оборудования, максимальная прибыль за 5 лет составит денежных единиц.

Для нахождения оптимальной политики создадим форму аналогичную изображенной на Рис. 4.

· Поместим курсор в ячейку В25.

· Обращаемся к Мастер функций (значок или на верхней панели).

· В окне Категория выбираем Логические.

· В окне Функция выбираем ЕСЛИ.

· Нажимаем OK.

· Заполняем поля в окне функции ЕСЛИ, используя формулу (1). (Рис.8)

 

Рис.8

 

· Нажимаем ОК и при помощи функции Автозаполнение заполняем остальные ячейки строки.

При заполнении остальных строк необходимо использовать следующую формулу.

Для заполнения ячейки В24 такжеиспользуем функцию ЕСЛИ (Рис.9) и Автозаполнение для ячеек С24-Н24. (Обратите внимание на абсолютную ссылку.)

Рис.9

 

Для удобства ячейки, соответствующие стратегии замены, следует залить каким-либо цветом и затем повторить заливку в предыдущей таблице.

После выполнения вышеописанных операций окно Excel будет выглядеть следующим образом. (Рис.10)

 

 

Рис.10

 

 

Эта таблица содержит много ценной информации и позволя­ет решать все семейство задач, в которое мы погружали исходную задачу.

Пусть, например, в начале первого года планового периода имеем оборудование возраста года. Разработаем «политику замен» на пятилетний период, доставляющую максимальную прибыль. Информация для этого имеется в таблице на Рис.10. Максимальная прибыль, которую можно получить за 5 лет при условии, что вначале первого года планового периода имелось оборудование возраста 2 года, находится в ячейке D14: .

Значение максимальной прибыли находится в зоне замен, это значит, что для достижения в течение 5 лет максимальной прибыли в начале первого года оборудование надо заменить. В течение первого года новое оборудо­вание постареет на год, т. е., заменив оборудование и проработав на нем 1 год, мы в начале второго года планового периода будем иметь оборудова­ние возраста 1 год. Из таблицы берем F ₂(1)= 75. Т.е. за два последних года планового периода можно получить максимальную прибыль 75 единиц, а за последний (пятый) год 89–75=14 единиц. Значение F ₂(1)= 75 распо­лагается в области сохранения, т. е. в начале второго года оборудование (возраста 1 год) надо сохранить, и, проработав на нем год, будем иметь оборудова­ние возраста 2 года. Находим значение F ₃(2) = 54. Оно находится в области замены. Следовательно, к началу четвертого года будем иметь оборудова­ние возраста 1 год. Находим значение Оно находится в области сохранения. Находим значение

Полученное решение можно оформить в виде следующей таблицы.

 

k- номер года планового периода длиной N лет
Реальный возраст оборудования на начало года
Максимально возможная прибыль за последние N- k +1 лет периода
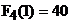
Решение	Зам.	Сохр.	Зам.	Сохр.	Сохр.
Возраст оборудования на начало года после принятия решения
Прибыль за год

 

Сравним полученное решение с ситуацией, когда сравнительно новое () оборудование не будет заменяться все пять лет.

Общая прибыль за пять лет составит

денежных единицы, оборудование будет иметь возраст 7 лет, и его остаточная стоимость не будет превосходить двух единиц. Если же придерживаться выработанной политики (замена; сохранение; замена; сохранение; сохранение), то прибыль будет равна 89 денежным единицам, оборудование к концу периода будет иметь возраст 3 года и его остаточная стоимость будет равна 9 единицам.

Таблица на Рис.10 содержит информацию для решения и других задач. Из нее можно найти оптимальную стратегию замены оборудования с любым начальным состоянием от 0 до 6 лет и на любой плановый период, не превосходящий 5 лет. Например, решим задачу на плано­вый период в года, если вначале имелось оборудование возраста лет.

 

k- номер года планового периода длиной N лет
Реальный возраст оборудования на начало года
Максимально возможная прибыль за последние N- k +1 лет периода
Решение	Зам.	Сохр.	Сохр.	Сохр.
Возраст оборудования на начало года после принятия решения
Прибыль за год