В ЕГЭ задачи по банковским вкладам и кредитам включены во вторую часть работы. При решении задачи необходимо записать подробное ее решение. Анализируя решения задач указанного типа, приходим к выводу, что основные трудности возникают у учащихся при составлении математической модели (уравнения) указанной задачи.
Прежде чем приступить с учениками к разбору непосредственно задач из открытого банка ЕГЭ, необходимо вспомнить решение простейших банковских задач из курса математики основной школы.
Ниже подробно рассмотрены решения семи задач по банковским вкладам и кредитам. Решения нескольких задач представлены в формате видеоуроков. Данные видеозаписи можно использовать на уроках при объяснении учащимся принципа решения задач данного вида.
Задача 1 (из учебника Н.Я. Виленкина Математика 6 класс): Банк купил несколько акций завода и через год продал их за 576,8 млн рублей, получив 3% прибыли. Какую сумму банк затратил на приобретение акций?
Решение: Сумма 576,8 млн рублей состоит из суммы которую банк затратил на приобретение акций (100%) и суммы дохода 3%. Таким образом, сумма 576,8 млн рублей составляет 103% от первоначальной стоимости акций.
Задачу можно решить в одно действие, но сейчас нам важно составить модель того, как происходили накопления.
Пусть А млн рублей – сумма которую банк затратил на приобретение акций (100%)
Тогда сумма акций через год будет равна выражению
(А + (3% от А)) Обозначим это выражение (*)
Узнаем сколько млн рублей составляют 3% от А. Для этого нам необходимо А:100 – узнаем сколько млн рублей составляет 1% от А, а затем полученное число умножаем на 3. Или, воспользуемся правилами из учебника математики пятого и шестого классов:
|
|
1) Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100;
2) чтобы найти дробь от числа, нужно умножить число на эту дробь.
То есть, 1) 3% = 0,03; 2) А∙0,03.
Итак, наше выражение (*) теперь примет вид:
А + 0,03∙А = 576,8
Теперь остается решить линейной уравнение с неизвестным А.
1,03А = 576,8
А = 560
Ответ: 560 млн рублей.
Замечание: Здесь важно заметить, что через год сумма акций будет составлять 1,03А. Если обозначить процент дохода r%, то данную сумму в общем виде можно записать следующим образом:
млн рублей (**)
Задача 2: В банк внесен вклад 550 млн рублей под 11% годовых. Какая сумма денег будет на счете через год? Через три года?
Решение: 1. Для ответа на первый вопрос задачи можно использовать формулу (**) из решения предыдущей задачи:
r % - 11 %, A = 550 --->
.
Для ответа на второй вопрос задачи можно так же использовать формулу (**): сначала для определения суммы вклада через два года, а затем через три.
– через два года
– через три года.
Следует обратить внимание на то, что через каждый год сумма вклада увеличивается на 11%, т.е. начисленные проценты остаются на счете вклада. Поэтому в формуле (**) при вычислении суммы вклада через два года и через три года подставляем разные значения А.
2. Ответ на второй вопрос задачи можно получить иначе – пропустить числовые вычисления, составить формулу (модель) для определения суммы вклада через три года в общем виде. Этот способ более трудоемкий, однако нам необходимо его разобрать для того, что увидеть схему (алгоритм) решения более сложных задач. Итак,
Через один год: (A + 0,001∙r∙A) или 
|
|
Через два года: 
Через три года: 
Подставив значения А = 550, r = 11 в последнюю формулу, получим:
млн рублей – сумма вклада на счете через три года
Ответ: 610,5 млн рублей; 752,19705 млн рублей.
Замечание: Составив формулы для определения суммы вклада через год, через два и через три года важно заметить закономерность: каждый год степень множителя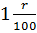 
увеличивается ровно на 1. Таким образом, можно посчитать суммы вклада через любое количество лет. Для наглядности составим таблицу:
| Год | Сумма вклада | Сумма вклада через год |
| А |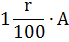 
| |
|
| 
| |
| 
| |
|
| 
| |
| ……… | ||
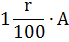
| n | 
| 
|
Задача 3 (Диагностическая работа СтатГрад, январь 2017): По бизнес-плану четырехлетний проект предполагает начальное вложение – 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй года, а также целое число m млн рублей и в третий, и в четвертый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее такое значение m, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Решение:
Решение данной задачи представлено в видеоуроке с которым можно ознакомиться перейдя по ссылке:
https://www.youtube.com/watch?v=HfwWbhQVCck&t=40s&spfreload=10
Задача 4 (с сайта www.egemaximum.ru): 31 декабря текущего года Алексей взял в банке 9282000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), а затем Алексей переводит в банк x рублей. Какой должна быть сумма х, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за 4 года)?
|
|
Решение: Составим следующую таблицу:
| Год кредитования | Кредит (основной долг) | Кредит + 10% | Выплата | Остаток основного долга |
| А | А+0,1А | Х | 1,1А – Х | |
| 1,1А – Х | *= 1,21А – 1,1Х | Х | 1,21А – 2,1Х | |
| 1,21А – 2,1Х | 1,331А – 2,31Х | Х | 1,331А – 3,31Х | |
| 1,331А – 3,31Х | 1,4641А – 3,641Х | Х | 1,4641А – 4,641Х |
где А – 9282000 рублей, r% - 10% годовых (ставка кредита), Х – ежегодный платеж.
* = 1,1А – Х + (1,1А – Х)∙0,1 = 1,1А – Х + 0,11А – 0,1Х = 1,21А – 1,1Х (аналогичные рассуждения для третьего и четвертого года кредитования. Для тренировки необходимо дать возможность учащимся просчитать эти графы самостоятельно и сверить с ответом).
В последний год кредитования остаток основного долга после последней выплаты должен быть равен нулю (долг полностью выплачен), т.е. 1,4641А – 4,641Х = 0.
Подставим в это равенство 9282000 вместо А, получим:
1,4641∙9282000 – 4,641Х = 0
13589776,2 = 4,641Х
Х = 13589776,2: 4,641= 2928200
Таким образом, ежегодный платеж равен 2928200 рублей
Ответ: 2928200 рублей
Задача 5 (ЕГЭ, 2016): 15-го января планируется взять кредит в банке на сумму 1 млн рублей на 6 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 |
Найдите наименьшее значение r, при котором общая сумма выплат будет составлять более 1,25 млн рублей.
Решение:
Решение данной задачи представлено в видеоуроке с которым можно ознакомиться перейдя по ссылке:
https://www.youtube.com/watch?v=Ab1MPFAu9nU&t=5s
Задача 6 (ЕГЭ, 2016): В июле 2016 года планируется взять кредит в банке на S млн рублей, где S – целое число, на 4 года. Условия его возврата таковы:
- каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
| Год | |||||
| Долг (в млн рублей) | S | 0,8S | 0,5S | 0,1S |
Найдите наибольшее значение S, чтобы общая сумма выплат была меньше 50 млн рублей?
Решение:
Решение данной задачи представлено в видеоуроке с которым можно ознакомиться перейдя по ссылке:
https://www.youtube.com/watch?v=Bnt2ruCsF5k&t=35s
Задача 7 (Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ, 2016): В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?
Решение:
Решение данной задачи представлено в видеоуроке с которым можно ознакомиться перейдя по ссылке:
https://www.youtube.com/watch?v=Yn0_lYE1kcs&t=645s