1.Научно - методическое обоснование темы:
Случайные погрешности измерений обусловлены неконтролируемыми причинами и представляют собой разность между результатами измерений величин и соответствующими истинными значениями этих величин. Наличие случайных погрешностей приводит к тому, что результат измерения представляет собой случайную величину, для описания которой могут быть применены статистические методы. Эти методы различаются в зависимости
от того, погрешности каких измерений — прямых или косвенных — рассматриваются.
2.Краткая теория:
Косвенными называют измерения, когда результат получают не непосредственно, а путем расчетов по математическим формулам, в которые входят непосредственно измеряемые величины.
Пусть искомая величина у связана некоторой функциональной зависимостью с непосредственно измеряемыми величинами:
причем каждая из величин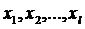 
измерена п раз и проведена их статистическая обработка, в результате которой получены средние значения
, а также средние квадратические отклонения этих средних значений 
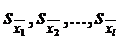по формулам:
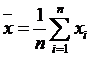, (1)
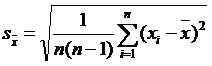, (2)
Тогда в качестве наилучшей точечной оценки косвенно измеряемой величины принимают величину
, (3)
а значение среднего квадратического отклонения для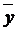 
вычисляют по формуле
, (4)
где частные производные находят при значениях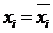 
.
Абсолютную погрешность косвенного измерения величины у вычисляют по формуле
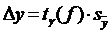, (5)
где 
- коэффициент для заданной доверительной вероятности γ и числа степеней свободы f = n —1.
Результат косвенного измерения обычно представляют в виде
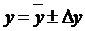, (6)
а относительную погрешность результата определяют по формуле
|
|
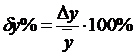, (7)
Пример. При четырех измерениях массы М и объема V таблетки получили результаты, представленные в следующей таблице:
Таблица 1
| M, г | 0,200 | 0,202 | 0,198 | 0,200 |
| V, см3 | 0,395 | 0,400 | 0,405 | 0,400 |
При доверительной вероятности γ = 0,95 найти интервальную оценку средней плотности вещества таблетки.
Решение. Поскольку средняя плотность вещества тела D связана с массой тела М и его объемом V соотношением
D = М/V, (8)
для оценки средней плотности вещества таблетки необходимо, прежде всего, по формуле(1) вычислить средние значения массы таблетки и ее объема:
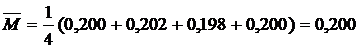г;
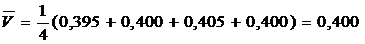см3.
Полученные результаты позволяют в соответствии с формулой (3) найти точечную оценку средней плотности вещества таблетки:
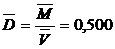г/см3, (9)
Найдем частные производные функции (8):
; 
.
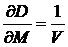которые при подстановке значени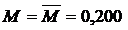й 
и 
окажутся равными
; 
.
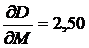В соответствии с формулой (2) найдем средние квадратические отклонения средних значений массы таблетки и ее объема:
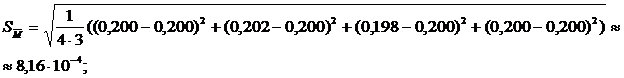
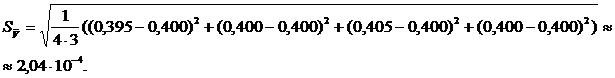
Используя эти значения, а также найденные ранее значения частных производных, в соответствии с формулой (4) получим среднее квадратическое отклонение среднего значения искомой плотности:
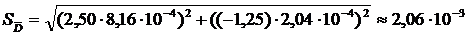г/см3.
По таблице найдем значение коэффициента Стьюдента:
.
Используя полученные значения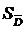 
и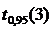 
, в соответствии с формулой (5) найдем абсолютную погрешность косвенного измерения плотности:
г/см3.
Согласно (6), окончательно интервальную оценку искомой плотности представим в виде:
|
|
D =(0,500 ± 0,007) г/см3.
Относительную погрешность косвенного измерения плотности получим в соответствии с (7):
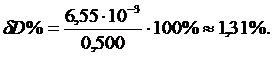
3. Цель деятельности студентов на занятии:
Студент должен знать:
1. Понятия прямых и косвенных измерений.
2. Оценки случайных погрешностей косвенных измерений.
Студент должен уметь:
1. Находить интервальные оценки косвенно измеряемых величин.
2. Находить абсолютную и относительную погрешности косвенного измерения величин.
4. Содержание обучения:
Теоретическая часть:
1. Косвенные измерения.
2. Оценка случайных погрешностей косвенных измерений.
Практическая часть:
1.При 12-кратном измерении температуры раствора серной кислоты получены следующие значения: 20,0; 20,3; 20,0; 20,2;19,5; 20,5; 19,7; 20,0; 20,4; 20,0; 19,6; 19,8. Дать точечную и интервальную (с доверительной вероятностью 0,95) оценки истинной концентрации раствора и вычислить относительную погрешность измерения концентрации.
2.При 5- кратном измерении диаметра Д и высоты Н цилиндра получены следующие результаты (в см):
| Д | 4,00 | 4,05 | 3,95 | 3,90 | 4,00 |
| Н | 5,1 | 5,0 | 5,0 | 4,9 | 5,1 |
Вычислить относительную погрешность измерения объема.
3.При семи измерениях массы М и объема V таблетки получены результаты, представленные в следующей таблице:
| М, г | 0,200 | 0,197 | 0,199 | 0,200 | 0,201 | 0,198 | 0,202 |
| V, см3 | 0,500 | 0,495 | 0,500 | 0,505 | 0,495 | 0,500 | 0,505 |
При доверительной вероятности γ = 0,95 найти интервальную оценку средней плотности вещества таблетки.
5. Перечень вопросов для проверки исходного уровня знаний:
1. Чем обусловлены случайные погрешности измерений?
|
|
2. Какие измерения называются прямыми?
3. Что понимают под косвенными измерениями?
4. Что является наилучшей точечной оценкой истинного значения величины при прямых измерениях?
5. Запишите формулы для оценок случайных погрешностей прямых измерений.
6. Перечень вопросов для проверки конечного уровня знаний:
1. Что принимают за наилучшую точечную оценку косвенно измеряемой величины?
2. Запишите формулу среднего квадратического отклонения для точечной оценки косвенно измеряемой величины.
3. По каким формулам вычисляются абсолютная и относительная погрешности косвенных измерений?
7. Хронокарта учебного занятия:
1. Организационный момент – 5 мин.
2. Разбор темы – 20 мин.
3.Решение ситуационных задач - 40 мин.
4. Текущий контроль знаний -30 мин.
5. Подведение итогов занятия – 5 мин.
8. Перечень учебной литературы к занятию:
1. Морозов Ю.В. Основы высшей математики и статистики. М., «Медицина», 2004, § 9.4.
2. Павлушков И.В. и др. Основы высшей математики и математической статистики. М., «ГЭОТАР-Медиа», 2006, § 8.2.3.