Перпендикулярные прямые в пространстве

План лекции

Вопрос 1. Перпендикулярные прямые в пространстве.

Вопрос 2. Параллельные прямые, перпендикулярные к плоскости.

Вопрос 3. Признак перпендикулярности прямой и плоскости

Вопрос 1. Перпендикулярные прямые в пространстве.

Две прямые называются перпендикулярными, если угол между ними равен 90°. Обозначение .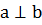

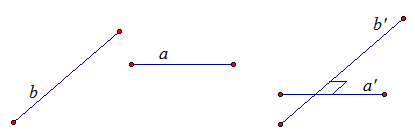
Рассмотрим прямые а и b. Они могут пересекаться, скрещиваться, быть параллельными. Для того чтобы построить угол между ними нужно выбрать точку и через нее провести прямую а’, параллельную прямой а, и прямую b’, параллельную прямой b. Прямые а’ и b’ пересекаются. Угол между ними и есть угол между прямыми а и b. Если угол равен 90°, то прямые а и b перпендикулярны.

Лемма. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. Обозначение .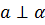

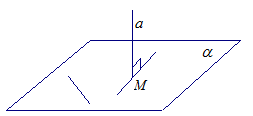
Свойство Если 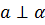, то .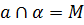

Вопрос 2. Параллельные прямые, перпендикулярные к плоскости.

Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярная к этой плоскости.

Обратная теорема. Если две прямые перпендикулярны к плоскости, то они параллельны.

Теорема о прямой, перпендикулярной к плоскости.

Утверждение. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.

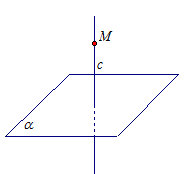
Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Задача 1. Дан параллелепипед ABCDA₁B₁C₁D₁. Докажите, что 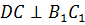и 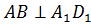, если .

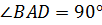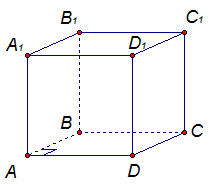
Доказательство. ABCD – прямоугольник, так как в параллелограмме ABCD угол .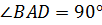

Прямая В₁С₁ параллельна прямой ВС, а прямая ВС перпендикулярна прямой DС. Значит, по лемме, прямая DС перпендикулярна В₁С₁.

Прямая АВ перпендикулярна прямой ВС, а ВС параллельна прямой A₁D₁. Значит, по лемме, прямая АВ перпендикулярна A₁D₁. Задача доказана.

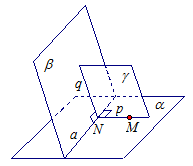
Задача 2. Докажите, что если две плоскости α и β перпендикулярны к прямой а, то они параллельны.

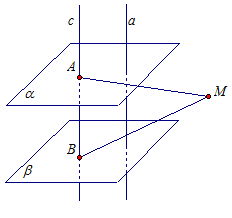
Доказательство: Проведем прямую с параллельно прямой а. По лемме, если одна из двух параллельных прямых пересекает плоскость, то и другая прямая тоже пересекает плоскость. Прямая а пересекает плоскости α и β по условию. Значит прямая с пересекает плоскость α в некоторой точке А и плоскость β в точке В.Прямая а перпендикулярна плоскостям α и β, а значит и параллельная ей прямая с перпендикулярна плоскостям α и β.

Предположим, что плоскости α и β пересекаются. Точка М – общая точка плоскостей α и β. Но тогда в треугольнике АМВ угол МАВ равен 90° и угол АВМ равен 90°, что невозможно. Значит, предположение о том, что плоскости α и β пересекаются было неверным. Значит, плоскости α и β параллельны.

Вопрос 3. Признак перпендикулярности прямой и плоскости

Теорема. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Доказательство.

Пусть нам дана плоскость α. В этой плоскости лежат две пересекающиеся прямые p и q. Прямая а перпендикулярна прямой p и прямой q. Нам нужно доказать, что прямая а перпендикулярна плоскости α, то есть, что прямая а перпендикулярна любой прямой, лежащей в плоскости α.

Напоминание.

Для доказательства нам нужно вспомнить свойства серединного перпендикуляра к отрезку. Серединный перпендикуляр р к отрезку АВ – это геометрическое место точек, равноудаленных от концов отрезка. То есть, если точка С лежит на серединном перпендикуляре р, то АС = ВС.

Пусть точка О – точка пересечения прямой а и плоскости α. Без ограничения общность, будем считать, что прямые p и q пересекаются в точке О. Нам нужно доказать перпендикулярность прямой а к произвольной прямой m из плоскости α.

Проведем через точку О прямую l, параллельно прямой m. На прямой а отложим отрезки ОА и ОВ, причем ОА = ОВ, то есть точка О – середина отрезка АВ. Проведем прямую PL, .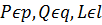

Прямая р перпендикулярна прямой а (из условия), 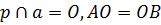(по построению). Значит, р – серединный перпендикуляр к отрезку АВ. Точка Р лежит на прямой р. Значит, РА = РВ.

Прямая q перпендикулярна прямой а (из условия), 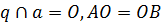(по построению). Значит, q – серединный перпендикуляр к отрезку АВ. Точка Q лежит на прямой q. Значит, QА = QВ.

Треугольники АРQ и ВРQ равны по трем сторонам (РА = РВ, QА = QВ, РQ – общая сторона). Значит, углы АРQ и ВРQ равны.

Треугольники АPL и BPL равны по углу и двум прилежащим сторонам (∠ АРL = ∠ ВРL, РА = РВ, PL – общая сторона). Из равенства треугольников получаем, что AL = BL.

Рассмотрим треугольник ABL. Он равнобедренный, так как AL = BL. В равнобедренном треугольнике медиана LО является и высотой, то есть прямая LО перпендикулярна АВ.

Мы получили, что прямая а перпендикулярна прямой l, а значит, и прямой m, что и требовалось доказать.

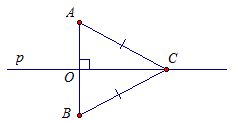
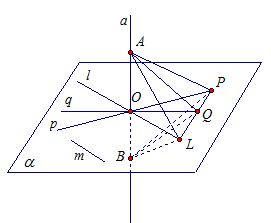
Задача 3. Точки А, М, О лежат на прямой, перпендикулярной к плоскости α, а точки О, В, С и D лежат в плоскости α. Какие из следующих углов являются прямыми: ?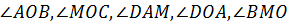

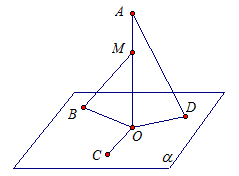
Решение

Рассмотрим угол 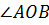. Прямая АО перпендикулярна плоскости α, а значит, прямая АО перпендикулярна любой прямой, лежащей в плоскости α, в том числе прямой ВО. Значит, .

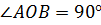Рассмотрим угол 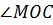. Прямая АО перпендикулярна прямой ОС, значит,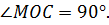

Рассмотрим угол 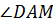. Прямая АО перпендикулярна прямой ОD, значит, 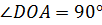. Рассмотрим треугольник DAO. В треугольнике может быть только один прямой угол. Значит, угол DAM – не является прямым.

Рассмотрим угол 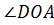. Прямая АО перпендикулярна прямой ОD, значит,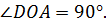

Рассмотрим угол 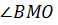. Это угол в прямоугольном треугольнике BMO, он не может быть прямым, так как угол МОВ – прямой.

Ответ: 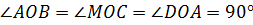.