кафедра информатики и вычислительной техники
Эконометрика
Методические указания
по самостоятельной работе студентов
направления подготовки 38.03.01 (080100.62) Экономика
степень выпускников: бакалавр
Киров
Рассмотрено на заседании кафедры информатики и вычислительной техники, протокол № 1 от 9 сентября 2014 г.
Утверждено на заседании учебно-методического совета, протокол № 87 от 20 октября 2014 г.
Эконометрика: Методические указания / Сост. М.Ю. Здоровенко. – Киров: ВСЭИ, 2014. – 20 с.
Методические указания разработаны в соответствии с учебной программой дисциплины и предназначены для студентов, обучающихся по направлению подготовки 38.03.01 (080100.62) Экономика (степень выпускника: бакалавр)
© Вятский социально-экономический
институт (ВСЭИ), 2014
1. Цели и задачи контрольной работы
Цель контрольной работы: изучение основных понятий и задач эконометрического моделирования.
Задачи контрольной работы:
1. Формирование навыков применения основных приемов решения практических задач.
2. Формирование умений проводить эконометрические исследования, обрабатывать и анализировать статистические данные, строить и анализировать эконометрические регрессионные модели.
2. Требования к результатам контрольной работы
В результате выполнения контрольной работы студент должен:
Знать:
- основные показатели качества регрессионной модели;
- основные этапы построения регрессионной модели;
- основные этапы анализа качества регрессионной модели.
Уметь:
- проводить анализ первичных статистических данных;
- на основе статистических данных строить регрессионную модель;
- анализировать качество и адекватность модели;
- содержательно интерпретировать результаты эконометрической обработки данных.
Владеть:
- навыками построения регрессионной модели;
- методами анализа регрессионных моделей.
3. Объем самостоятельной работы студента
Самостоятельная работа студента составляет 1,5 зачетные единицы по очной форме обучения, 2,5 зачетные единицы по заочной форме обучения.
Выполнение контрольной работы предполагает самостоятельную работу студента по темам 1.2, 1.3 первого раздела, а также по всем темам 2-5 разделов учебной программы
4. Варианты контрольной работы
1. Вариант
Технологические изменения в экономике США 1909 - 1928 гг. (Модель Солоу):
| Год | |||||||
| Q | 0,623 | 0,616 | 0,647 | 0,652 | 0,680 | 0,682 | 0,669 |
| K | 2,06 | 2,10 | 2,17 | 2,21 | 2,23 | 2,20 | 2,26 |
| A | 1,000 | 0,983 | 1,021 | 1,023 | 1,064 | 1,071 | 1,041 |
| Год | |||||||
| Q | 0,700 | 0,679 | 0,729 | 0,767 | 0,721 | 0,770 | 0,788 |
| K | 2,34 | 2,21 | 2,22 | 2,47 | 2,58 | 2,55 | 2,49 |
| A | 1,076 | 1,065 | 1,142 | 1,157 | 1,069 | 1,146 | 1,183 |
| Год | ||||||
| Q | 0,809 | 0,836 | 0,872 | 0,869 | 0,871 | 0,874 |
| K | 2,61 | 2,74 | 2,81 | 2,87 | 2,93 | 3,02 |
| A | 1,196 | 1,215 | 1,254 | 1,241 | 1,235 | 1,226 |
q - совокупное производство в расчете на 1 человеко-час (производительность труда);
k - капиталовооруженность труда;
A - технологический индекс.
Задача 1
Используя данные таблицы построить двумерные регрессионные модели:
| модель 1 | модель 2 |
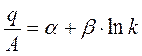 здесь
здесь  , ,
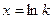
| 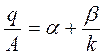 здесь
здесь  , ,
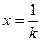
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать дисперсии оценок 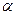 и
и 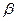 ;
;
4) рассчитать коэффициент корреляции, коэффициент детерминации и скорректированный коэффициент детерминации;
5)проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом;
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
Сделать выводы
Сравнить качество построенных моделей. Какая модель предпочтительнее?
Задача 2
Используя данные таблицы построить трехмерные регрессионные модели:
| модель 1 | модель 2 |
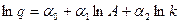 здесь
здесь 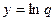 , ,
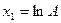
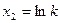
| 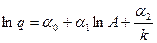 здесь
здесь  , ,
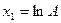
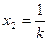
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать коэффициент детерминации и скорректированный коэффициент детерминации;
4) рассчитать парные коэффициенты корреляции и частные коэффициенты корреляции;
5) проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом.
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
7) проверить модель на наличие мультиколинеарности;
8) проверить, является ли модель гетероскедастичной.
Сделать выводы.
Сравнить качество построенных моделей. Какая модель предпочтительнее?
2. Вариант
Технологические изменения в экономике США 1915 - 1934 гг. (МодельСолоу):
| Год | |||||||
| Q | 0,669 | 0,700 | 0,679 | 0,729 | 0,767 | 0,721 | 0,770 |
| K | 2,26 | 2,34 | 2,21 | 2,22 | 2,47 | 2,58 | 2,55 |
| A | 1,041 | 1,076 | 1,065 | 1,142 | 1,157 | 1,069 | 1,146 |
| Год | |||||||
| Q | 0,788 | 0,809 | 0,836 | 0,872 | 0,869 | 0,871 | 0,874 |
| K | 2,49 | 2,61 | 2,74 | 2,81 | 2,87 | 2,93 | 3,02 |
| A | 1,183 | 1,196 | 1,215 | 1,254 | 1,241 | 1,235 | 1,226 |
| Год | ||||||
| Q | 0,895 | 0,880 | 0,904 | 0,879 | 0,869 | 0,921 |
| K | 3,06 | 3,30 | 3,33 | 3,28 | 3,10 | 3,00 |
| A | 1,251 | 1,197 | 1,226 | 1,198 | 1,211 | 1,298 |
q - совокупное производство в расчете на 1 человеко-час (производительность труда);
k - капиталовооруженность труда;
A - технологический индекс.
Задача 1
Используя данные таблицы построить двумерные регрессионные модели:
| модель 1 | модель 2 |
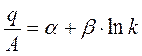 здесь
здесь  , ,
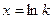
| 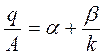 здесь
здесь  , ,
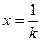
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать дисперсии оценок 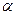 и
и 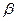 ;
;
4) рассчитать коэффициент корреляции, коэффициент детерминации и скорректированный коэффициент детерминации;
5)проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом;
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
Сделать выводы
Сравнить качество построенных моделей. Какая модель предпочтительнее?
Задача 2
Используя данные таблицы построить трехмерные регрессионные модели:
| модель 1 | модель 2 |
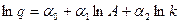 здесь
здесь 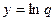 , ,
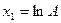
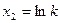
| 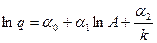 здесь
здесь  , ,
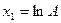
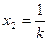
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать коэффициент детерминации и скорректированный коэффициент детерминации;
4) рассчитать парные коэффициенты корреляции и частные коэффициенты корреляции;
5) проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом.
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
7) проверить модель на наличие мультиколинеарности;
8) проверить, является ли модель гетероскедастичной.
Сделать выводы.
Сравнить качество построенных моделей. Какая модель предпочтительнее?
3. Вариант
Технологические изменения в экономике США 1920 – 1939 гг. (МодельСолоу):
| Год | |||||||
| Q | 0,721 | 0,770 | 0,788 | 0,809 | 0,836 | 0,872 | 0,869 |
| K | 2,58 | 2,55 | 2,49 | 2,61 | 2,74 | 2,81 | 2,87 |
| A | 1,069 | 1,146 | 1,183 | 1,196 | 1,215 | 1,254 | 1,241 |
| Год | |||||||
| Q | 0,871 | 0,874 | 0,895 | 0,880 | 0,904 | 0,879 | 0,869 |
| K | 2,93 | 3,02 | 3,06 | 3,30 | 3,33 | 3,28 | 3,10 |
| A | 1,235 | 1,226 | 1,251 | 1,197 | 1,226 | 1,198 | 1,211 |
| Год | ||||||
| Q | 0,921 | 0,943 | 0,982 | 0,971 | 1,000 | 1,034 |
| K | 3,00 | 2,87 | 2,72 | 2,71 | 2,78 | 2,66 |
| A | 1,298 | 1,349 | 1,429 | 1,415 | 1,445 | 1,514 |
q - совокупное производство в расчете на 1 человеко-час (производительность труда);
k - капиталовооруженность труда;
A - технологический индекс.
Задача 1
Используя данные таблицы построить двумерные регрессионные модели:
| модель 1 | модель 2 |
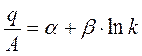 здесь
здесь  , ,
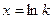
| 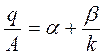 здесь
здесь  , ,
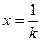
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать дисперсии оценок 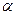 и
и 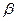 ;
;
4) рассчитать коэффициент корреляции, коэффициент детерминации и скорректированный коэффициент детерминации;
5)проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом;
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
Сделать выводы
Сравнить качество построенных моделей. Какая модель предпочтительнее?
Задача 2
Используя данные таблицы 3 построить трехмерные регрессионные модели:
| модель 1 | модель 2 |
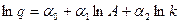 здесь
здесь 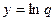 , ,
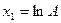
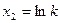
| 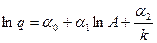 здесь
здесь  , ,
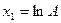
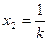
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать коэффициент детерминации и скорректированный коэффициент детерминации;
4) рассчитать парные коэффициенты корреляции и частные коэффициенты корреляции;
5) проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом.
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
7) проверить модель на наличие мультиколинеарности;
8) проверить, является ли модель гетероскедастичной.
Сделать выводы.
Сравнить качество построенных моделей. Какая модель предпочтительнее?
4. Вариант
Технологические изменения в экономике США 1925 - 1944 гг. (МодельСолоу):
| Год | |||||||
| Q | 0,872 | 0,869 | 0,871 | 0,874 | 0,895 | 0,880 | 0,904 |
| K | 2,81 | 2,87 | 2,93 | 3,02 | 3,06 | 3,30 | 3,33 |
| A | 1,254 | 1,241 | 1,235 | 1,226 | 1,251 | 1,197 | 1,226 |
| Год | |||||||
| Q | 0,879 | 0,869 | 0,921 | 0,943 | 0,982 | 0,971 | 1,000 |
| K | 3,28 | 3,10 | 3,00 | 2,87 | 2,72 | 2,71 | 2,78 |
| A | 1,198 | 1,211 | 1,298 | 1,349 | 1,429 | 1,415 | 1,445 |
| Год | ||||||
| Q | 1,034 | 1,082 | 1,122 | 1,136 | 1,180 | 1,265 |
| K | 2,66 | 2,63 | 2,58 | 2,64 | 2,62 | 2,63 |
| A | 1,514 | 1,590 | 1,660 | 1,665 | 1,692 | 1,812 |
q - совокупное производство в расчете на 1 человеко-час (производительность труда);
k - капиталовооруженность труда;
A - технологический индекс.
Задача 1
Используя данные таблицы 4 построить двумерные регрессионные модели:
| модель 1 | модель 2 |
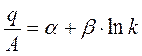 здесь
здесь  , ,
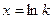
| 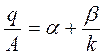 здесь
здесь  , ,
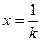
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать дисперсии оценок 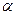 и
и 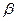 ;
;
4) рассчитать коэффициент корреляции, коэффициент детерминации и скорректированный коэффициент детерминации;
5)проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом;
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
Сделать выводы
Сравнить качество построенных моделей. Какая модель предпочтительнее?
Задача 2
Используя данные таблицы 4 построить трехмерные регрессионные модели:
| модель 1 | модель 2 |
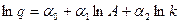 здесь
здесь 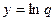 , ,
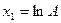
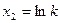
| 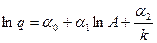 здесь
здесь  , ,
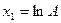
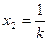
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать коэффициент детерминации и скорректированный коэффициент детерминации;
4) рассчитать парные коэффициенты корреляции и частные коэффициенты корреляции;
5) проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом.
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
7) проверить модель на наличие мультиколинеарности;
8) проверить, является ли модель гетероскедастичной.
Сделать выводы.
Сравнить качество построенных моделей. Какая модель предпочтительнее?
5. Вариант
Технологические изменения в экономике США 1930 - 1949 гг. (МодельСолоу):
| Год | |||||||
| Q | 0,880 | 0,904 | 0,879 | 0,869 | 0,921 | 0,943 | 0,982 |
| K | 3,30 | 3,33 | 3,28 | 3,10 | 3,00 | 2,87 | 2,72 |
| A | 1,197 | 1,226 | 1,198 | 1,211 | 1,298 | 1,349 | 1,429 |
| Год | |||||||
| Q | 0,971 | 1,000 | 1,034 | 1,082 | 1,122 | 1,136 | 1,180 |
| K | 2,71 | 2,78 | 2,66 | 2,63 | 2,58 | 2,64 | 2,62 |
| A | 1,415 | 1,445 | 1,514 | 1,590 | 1,660 | 1,665 | 1,692 |
| Год | ||||||
| Q | 1,265 | 1,296 | 1,215 | 1,194 | 1,221 | 1,275 |
| K | 2,63 | 2,66 | 2,50 | 2,50 | 2,55 | 2,70 |
| A | 1,812 | 1,850 | 1,769 | 1,739 | 1,767 | 1,809 |
q - совокупное производство в расчете на 1 человеко-час (производительность труда);
k - капиталовооруженность труда;
A - технологический индекс.
Задача 1
Используя данные таблицы 5 построить двумерные регрессионные модели:
| модель 1 | модель 2 |
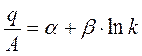 здесь
здесь  , ,
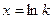
| 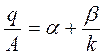 здесь
здесь  , ,
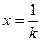
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать дисперсии оценок 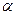 и
и 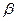 ;
;
4) рассчитать коэффициент корреляции, коэффициент детерминации и скорректированный коэффициент детерминации;
5)проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом;
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
Сделать выводы
Сравнить качество построенных моделей. Какая модель предпочтительнее?
Задача 2
Используя данные таблицы 5 построить трехмерные регрессионные модели:
| модель 1 | модель 2 |
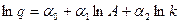 здесь
здесь 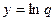 , ,
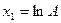
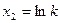
| 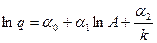 здесь
здесь  , ,
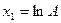
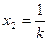
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать коэффициент детерминации и скорректированный коэффициент детерминации;
4) рассчитать парные коэффициенты корреляции и частные коэффициенты корреляции;
5) проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом.
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
7) проверить модель на наличие мультиколинеарности;
8) проверить, является ли модель гетероскедастичной.
Сделать выводы.
Сравнить качество построенных моделей. Какая модель предпочтительнее?
6. Вариант
Технологические изменения в экономике США 1909 - 1928 гг. (МодельСолоу):
| Год | |||||||
| Q | 0,623 | 0,616 | 0,647 | 0,652 | 0,680 | 0,682 | 0,669 |
| K | 2,06 | 2,10 | 2,17 | 2,21 | 2,23 | 2,20 | 2,26 |
| A | 1,000 | 0,983 | 1,021 | 1,023 | 1,064 | 1,071 | 1,041 |
| Год | |||||||
| Q | 0,700 | 0,679 | 0,729 | 0,767 | 0,721 | 0,770 | 0,788 |
| K | 2,34 | 2,21 | 2,22 | 2,47 | 2,58 | 2,55 | 2,49 |
| A | 1,076 | 1,065 | 1,142 | 1,157 | 1,069 | 1,146 | 1,183 |
| Год | ||||||
| Q | 0,809 | 0,836 | 0,872 | 0,869 | 0,871 | 0,874 |
| K | 2,61 | 2,74 | 2,81 | 2,87 | 2,93 | 3,02 |
| A | 1,196 | 1,215 | 1,254 | 1,241 | 1,235 | 1,226 |
q - совокупное производство в расчете на 1 человеко-час (производительность труда);
k - капиталовооруженность труда;
A - технологический индекс.
Задача 1
Используя данные таблицы 6 построить двумерные регрессионные модели:
| модель 1 | модель 2 |
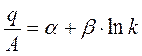 здесь
здесь  , ,
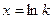
| 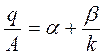 здесь
здесь  , ,
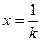
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать дисперсии оценок 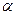 и
и 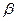 ;
;
4) рассчитать коэффициент корреляции, коэффициент детерминации и скорректированный коэффициент детерминации;
5)проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом;
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
Сделать выводы
Сравнить качество построенных моделей. Какая модель предпочтительнее?
Задача 2
Используя данные таблицы 6 построить трехмерные регрессионные модели:
| модель 1 | модель 2 |
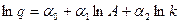 здесь
здесь 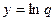 , ,
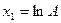
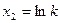
| 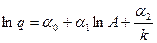 здесь
здесь  , ,
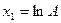
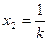
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать коэффициент детерминации и скорректированный коэффициент детерминации;
4) рассчитать парные коэффициенты корреляции и частные коэффициенты корреляции;
5) проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом.
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
7) проверить модель на наличие мультиколинеарности;
8) проверить, является ли модель гетероскедастичной.
Сделать выводы.
Сравнить качество построенных моделей. Какая модель предпочтительнее?
7. Вариант
Технологические изменения в экономике США 1915 - 1934 гг. (МодельСолоу):
| Год | |||||||
| Q | 0,669 | 0,700 | 0,679 | 0,729 | 0,767 | 0,721 | 0,770 |
| K | 2,26 | 2,34 | 2,21 | 2,22 | 2,47 | 2,58 | 2,55 |
| A | 1,041 | 1,076 | 1,065 | 1,142 | 1,157 | 1,069 | 1,146 |
| Год | |||||||
| Q | 0,788 | 0,809 | 0,836 | 0,872 | 0,869 | 0,871 | 0,874 |
| K | 2,49 | 2,61 | 2,74 | 2,81 | 2,87 | 2,93 | 3,02 |
| A | 1,183 | 1,196 | 1,215 | 1,254 | 1,241 | 1,235 | 1,226 |
| Год | ||||||
| Q | 0,895 | 0,880 | 0,904 | 0,879 | 0,869 | 0,921 |
| K | 3,06 | 3,30 | 3,33 | 3,28 | 3,10 | 3,00 |
| A | 1,251 | 1,197 | 1,226 | 1,198 | 1,211 | 1,298 |
q - совокупное производство в расчете на 1 человеко-час (производительность труда);
k - капиталовооруженность труда;
A - технологический индекс.
Задача 1
Используя данные таблицы 7 построить двумерные регрессионные модели:
| модель 1 | модель 2 |
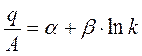 здесь
здесь  , ,
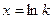
| 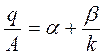 здесь
здесь  , ,
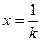
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать дисперсии оценок 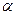 и
и 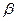 ;
;
4) рассчитать коэффициент корреляции, коэффициент детерминации и скорректированный коэффициент детерминации;
5)проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом;
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
Сделать выводы
Сравнить качество построенных моделей. Какая модель предпочтительнее?
Задача 2
Используя данные таблицы 7 построить трехмерные регрессионные модели:
| модель 1 | модель 2 |
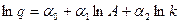 здесь
здесь 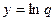 , ,
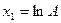
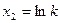
| 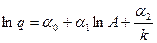 здесь
здесь  , ,
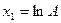
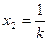
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать коэффициент детерминации и скорректированный коэффициент детерминации;
4) рассчитать парные коэффициенты корреляции и частные коэффициенты корреляции;
5) проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом.
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
7) проверить модель на наличие мультиколинеарности;
8) проверить, является ли модель гетероскедастичной.
Сделать выводы.
Сравнить качество построенных моделей. Какая модель предпочтительнее?
8. Вариант
Технологические изменения в экономике США 1920 – 1939 гг. (МодельСолоу):
| Год | |||||||
| Q | 0,721 | 0,770 | 0,788 | 0,809 | 0,836 | 0,872 | 0,869 |
| K | 2,58 | 2,55 | 2,49 | 2,61 | 2,74 | 2,81 | 2,87 |
| A | 1,069 | 1,146 | 1,183 | 1,196 | 1,215 | 1,254 | 1,241 |
| Год | |||||||
| Q | 0,871 | 0,874 | 0,895 | 0,880 | 0,904 | 0,879 | 0,869 |
| K | 2,93 | 3,02 | 3,06 | 3,30 | 3,33 | 3,28 | 3,10 |
| A | 1,235 | 1,226 | 1,251 | 1,197 | 1,226 | 1,198 | 1,211 |
| Год | ||||||
| Q | 0,921 | 0,943 | 0,982 | 0,971 | 1,000 | 1,034 |
| K | 3,00 | 2,87 | 2,72 | 2,71 | 2,78 | 2,66 |
| A | 1,298 | 1,349 | 1,429 | 1,415 | 1,445 | 1,514 |
q - совокупное производство в расчете на 1 человеко-час (производительность труда);
k - капиталовооруженность труда;
A - технологический индекс.
Задача 1
Используя данные таблицы 8 построить двумерные регрессионные модели:
| модель 1 | модель 2 |
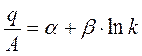 здесь
здесь  , ,
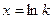
| 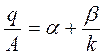 здесь
здесь  , ,
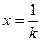
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать дисперсии оценок 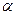 и
и 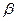 ;
;
4) рассчитать коэффициент корреляции, коэффициент детерминации и скорректированный коэффициент детерминации;
5)проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом;
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
Сделать выводы
Сравнить качество построенных моделей. Какая модель предпочтительнее?
Задача 2
Используя данные таблицы 8 построить трехмерные регрессионные модели:
| модель 1 | модель 2 |
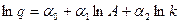 здесь
здесь 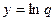 , ,
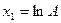
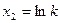
| 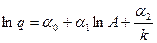 здесь
здесь  , ,
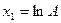
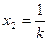
|
Для каждой модели следует:
1) построить уравнение регрессии;
2) рассчитать общую дисперсию, объясненную и необъясненную регрессией части дисперсии;
3) рассчитать коэффициент детерминации и скорректированный коэффициент детерминации;
4) рассчитать парные коэффициенты корреляции и частные коэффициенты корреляции;
5) проверить гипотезы о незначимости коэффициентов модели и о незначимости регрессии в целом.
6) найти доверительные интервалы для параметров регрессии на уровне значимости 95%.
7) проверить модель на наличие мультиколинеарности;
8) проверить, является ли модель гетероскедастичной.
Сделать выводы.
Сравнить качество построенных моделей. Какая модель предпочтительнее?
9. Вариант
Технологические изменения в экономике США 1925 - 1944 гг. (МодельСолоу):
| Год | |||||||
| Q | 0,872 | 0,869 | 0,871 | 0,874 | 0,895 | 0,880 | 0,904 |
| K | 2,81 | 2,87 | 2,93 | 3,02 | 3,06 | 3,30 | 3,33 |
| A | 1,254 | 1,241 | 1,235 | 1,226 | 1,251 | 1,197 | 1,226 |
| Год | |||||||
| Q | 0,879 | 0,869 | 0,921 | 0,943 | 0,982 | 0,971 | 1,000 |
| K | 3,28 | 3,10 | 3,00 | 2,87 | 2,72 | 2,71 | 2,78 |
| A | 1,198 | 1,211 | 1,298 | 1,349 | 1,429 | 1,415 | 1,445 |
| Год | |||||||||
| Q | 1,034 | 1,082 | 1,122 | 1,136 | 1,180 | 1,265 | |||
| K | 2,66 | 2,63 | 2,58 | 2,64 | 2,62 | 2,63 | |||
| A | 1,514 | 1,590 | 1,660 | 1,665 | 1,692 | 1,812
<
Поиск по сайту©2015-2025 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-02-16 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |