1. 
Определить скорость точки 
в момент, соответствующий 
, 
, стержень 
вращается с угловой скоростью 
относительно оси 
, перпендикулярной плоскости рисунка, в которой происходит движение всех стержней.
2. 
В кривошипно-ползунном механизме кривошип длиной 
вращается с угловой скоростью 
. Длина шатуна 
равна 
. При заданном угле 
определить: 1) скорость ползуна 
; 2) положение точки 
шатуна , имеющей наименьшую скорость; 3) угловую скорость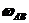 
шатуна.
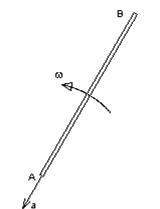
3. Стержень длиной 
совершает плоское движение. Найти ускорение точки , если ускорение точки 
равно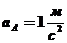 
, угловая скорость стержня 
, угловое ускорение 
.
4. 
Колесо катится по прямолинейному рельсу так, что скорость 
его центра постоянна. Определить ускорение точки обода колеса.
5. 
Прямоугольник 
со сторонами 
, 
совершает плоское движение. В данный момент ускорения 
. Определить ускорение точки 
, а также мгновенные угловые скорость и ускорение прямоугольника.
Занятие № 10
Моменты инерции
1. Вычислить момент инерции однородной равносторонней треугольной пластины массой 
, со стороной 
относительно оси 
, проходящей через ее вершину параллельно основанию.
2. 
Вычислить радиус инерции сплошного однородного цилиндра относительно оси , перпендикулярной его оси и отстоящей на расстоянии 
от центра масс . Радиус цилиндра 
, высота 
.
3. 
Найти главные моменты инерции однородного шара с радиусом 
, имеющего внутри сферическую полость с радиусом . Масса тела .
4. 
В вершинах квадрата со стороной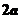 
расположены массы и . Найти компоненты тензора инерции относительно: а) осей 
; б) осей 
.
5. 
Массы и 
расположены в вершинах прямоугольного треугольника с катетам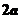и и 
. Найти главные оси и главные моменты инерции системы.
Занятие № 11
Динамика твердого тела
1. Однородный стержень массой и длиной укреплен так, что может вращаться вокруг вертикальной и горизонтальной осей, проходящих через его середину. Найти закон движения стержня.
2. 
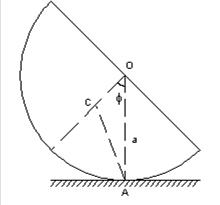Однородный полый полуцилиндр (половина цилиндрической поверхности, разрезанной вдоль плоскости симметрии) с массой и радиусом находится на абсолютно шероховатой горизонтальной плоскости и совершает линейные плоскопараллельные колебаний. Найти закон движения и период малых колебаний.
3. Найти частоту линейных колебаний неоднородного тонкого стержня с массой и длиной , концы которого скользят по расположенному в вертикальной плоскости гладкому обручу с радиусом . Плотность стержня линейно зависит от расстояния до одного из его концов.
4. Однородный диск массой скатывается без скольжения по наклонной плоскости с углом 
. Найти функцию Лагранжа, закон движения диска и реакцию плоскости.
5. Цилиндрическая тонкостенная бочка массой , заполненная невязкой жидкостью массой , скатывается с наклонной плоскости с углом . Найти закон движения и силу трения покоя. Проскальзыванием и моментами инерции днищ бочки пренебречь.
Занятие № 12
Уравнения Гамильтона
1. 
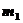Две частицы с массами 
и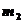 
соединены легким стержнем длиной и перемешаются по гладким сторонам неподвижного прямого угла, расположенного в вертикальной плоскости. Найти гамильтониан системы и канонические уравнения движения.
2. Два шарика с массам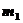и и 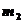соединенные легкой пружиной с жесткостью 
и длиной 
в ненапряженном состоянии, движутся по гладкой горизонтальной прямой, проходящей через центры шариков. Найти гамильтониан системы и канонические уравнения движения.
3. Найти канонические уравнения движения частицы с массой в однородном поле тяжести по гладкой поверхности кругового конуса с углом раствора 
и вертикальной осью симметрии. Раствор конуса направлен вверх.
4. Найти канонические уравнения движения частицы с массой в однородном поле тяжести по гладкой сфере с радиусом .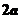
5. Найти канонические уравнения движения частицы с массой , в однородном поле тяжести, по гладкой плоскости с углом наклона к горизонту.
Занятие № 13