Рабочий участок проходной ВАХ транзистора аппроксимирован полиномом третьей степени iк=a0+a1(uбэ-U0)+a2(uбэ-U0)2+a3(uбэ-U0)3. Амплитуда гармонического напряжения на базе транзистора Е1=2в. Определить амплитуду первой гармоники спектра коллекторного тока, если а0= … ма, а1=… ма/в, а2=… ма/в2, а3=….. ма/в3(см. таблицу).
Определить амплитуды гармонических составляющих коллекторного тока в режиме работы транзистора с отсечкой при различных Θ и величине выходного импульса тока (см. таблицу). Определить кпд каскада и класс его работы.
Рабочий участок проходной ВАХ транзистора аппроксимирован полиномом второй степени iк=a0+a1(uбэ-U0)+a2(uбэ-U0)2. На базу транзистора подано напряжение uбэ(t)=U0+5(1+0,8cos(4πf1t))cos(2πf2t) Определить частоты спектра коллекторного тока, если а0=…ма, а1=…ма/в, а2=…ма/в2
Варианты:
| № | а0 | а1 | а2 | а3 | Е1 | Е2 | f1(кГц) | f2(кГц) | Θ | Iк max(А) |
| 0,1 | 2.84 | |||||||||
| 0,2 | 21.91 | |||||||||
| 0,5 | 2,2 | 4,75 | ||||||||
| 0,6 | 2,8 | 6,78 | ||||||||
| 0,2 | 2,6 | 9.51 | ||||||||
| 0,5 | 2,2 | 12.66 | ||||||||
| 0,4 | 2,3 | 5,8 | ||||||||
| 0,5 | 2,1 | 2,67 | ||||||||
| 0,1 | 2,14 | 3.45 | ||||||||
| 0,3 | 4,3 | 12.14 | ||||||||
| 0,25 | 2,5 | 2,79 | ||||||||
| 0,12 | 1,9 | 8.65 | ||||||||
| 0,14 | 1,85 | 8,45 | ||||||||
| 0,21 | 1,5 | 5,62 | ||||||||
| 0,31 | 1,87 | 11.58 | ||||||||
| 0,4 | 1,99 | 5.24 | ||||||||
| 0,27 | 1,36 | 11,85 | ||||||||
| 0,45 | 1,59 | 5,78 | ||||||||
| 0,21 | 2,15 | 3,95 | ||||||||
| 0,14 | 2,58 | 5,66 | ||||||||
| 0,11 | 2,55 | 8,12 | ||||||||
| 0,13 | 1,87 | 6,45 | ||||||||
| 0,22 | 2,56 | 2,89 | ||||||||
| 0,17 | 1,65 | 8,72 | ||||||||
| 0,19 | 1,35 | 5,47 | ||||||||
| 0,2 | 1,96 | 6,98 | ||||||||
| 0.2 | 1.4 | 6.85 | ||||||||
| 0.14 | 1.2 | 3.52 | ||||||||
| 0.26 | 1.84 | 21.85 | ||||||||
| 0.55 | 2.11 | 20.86 |
Контрольные вопросы.
|
|
- В каких случаях применяется аппроксимация?
- Что такое полином третьей или второй степени?
- Сколько получится гармоник выходного сигнала при аппроксимации полиномом третьей степени?
Практическая работа №5
Тема: Расчет и построение кода Шеннона-Фано.
Цель: Построение кодового «дерева» и вычисление коэффициента сжатия.
Теоретические сведения
Сжатие данных (data compression) - это алгоритм эффективного кодирования информации, при котором она занимает меньший объем памяти, нежели ранее. Мы избавляемся от избыточности (redundancy), т.е. удаляем из физического представления данных те биты, которые в действительности не требуются, оставляя только то количество битов, которое необходимо для представления информации в соответствии со значением энтропии. Существует показатель эффективности сжатия данных: коэффициент сжатия (compression ratio). Он вычисляется путем вычитания из единицы частного от деления размера сжатых данных на размер исходных данных и обычно выражается в процентах. Например, если размер сжатых данных равен 1000 бит, а несжатых - 4000 бит, коэффициент сжатия составит 75%, т.е. мы избавились от трех четвертей исходного количества битов.
|
|
Существует два основных типа сжатия данных: с потерями (lossy) и без потерь (lossless). Lossless- метод сжатия данных, когда распаковка упакованного файла приводит к созданию файла, который имеет в точности то же содержимое, что и оригинал перед его сжатием. И напротив, сжатие с потерями не позволяет при восстановлении получить те же исходные данные. Это кажется недостатком, но для определенных типов данных, таких как данные изображений и звука, различие между восстановленными и исходными данными не имеет особого значения: наши зрение и слух не в состоянии уловить образовавшиеся различия. В общем случае алгоритмы сжатия с потерями обеспечивают более эффективное сжатие, чем алгоритмы сжатия без потерь. Для примера можно сравнить предназначенный для хранения изображений формат с потерями JPEG с форматом без потерь GIF. Множество форматов потокового аудио и видео, используемых в Internet для загрузки мультимедиа-материалов, являются алгоритмами сжатия с потерями.
Алгоритм сжатия Шеннона-Фано является алгоритмом сжатия без потерь и называются кодированием с минимальной избыточностью (minimum redundancy coding).
Код Шеннона-Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
|
|
Пусть дан текстовый файл в котором символы встречаются с числом встречаемости из таблицы1.
Таблица1. Список узлов по алфавиту
| Символ | A | B | C | D | E | F |
| Число встречаемости |
Сумма чисел встречаемости символов равна 100.
Делим символы на две группы с примерно одинаковой встречаемостью:АСF с вероятностью 50 и BDE с такой же вероятностью. Это две ветви выходящих из корня.
Далее алгоритм повторяется. Группа ACF разбивается на две: С с встречаемостью 30 и AF с встречаемостью 20. Группа BDE – на BD и Е с соответствующими числами 25 и 25.
Алгоритм прекращается для одиночных символов и продолжается для групп. AF и BD делятся на две части. Дерево построено, присваиваем левому повороту 0-й бит, а правому -1-й бит.
A B C D E F (100)
0/ 1\
А С F(50) B D E(50)
0/ 1\ 0/ 1\
C(30) AF(20) E(25) BD(25)
0/ 1\ 0/ 1\
A(10) F(10) B(20) D(5)
Отсчет кода ведется от корня.
Таблица3. Кодовые последовательности
| Символ | A | B | C | D | E | F |
| Код |
Каждый символ изначально представлялся 8-ю битами(1байт), и при уменьшении числа битов уменьшается и размер выходного файла.
Сжатие складывается таким образом(таблица4):
Таблица 4.Расчет сжатия символов
| Частота | первоначально | После уплотнения | Уменьшено на |
| С 30 | 30х8=240 | 30х2=60 | |
| А 10 | 10х8=80 | 10х3=30 | |
| D 5 | 5х8=40 | 5х3=15 | |
| F 10 | 10х8=80 | 10х3=30 | |
| B 20 | 20х8=160 | 20х3=60 | |
| E 25 | 25х8=200 | 25х2=50 |
Первоначальный размер файла: 100байт = 800бит
Размер сжатого файла: 30 байт = 245 бит
Процент сжатия: 100-(245/800)х100 = 69%.
Порядок выполнения работы.
1. Взять данные для расчета согласно варианта задания в приложении.
2. Создать таблица списков узлов по алфавиту и встречаемости.
3. Построить кодовое дерево.
4. Заполнить таблицу кодовых последовательностей.
5. Рассчитать сжатие символов.
6. Рассчитать размер сжатого файла и процент сжатия.
Контрольные вопросы
- По алгоритму Шеннона-Фано, чаще встречаемым символам соответствует более……… код.
- Для чего применяется алгоритм сжатия.
- Меньше сжимаются символы …….. встречаемые.
Приложение. Варианты задания
| Номер варианта | Фраза для кодирования |
| У нас во дворе-подворье погода размокропогодилась | |
| Два дровосека, два дроворуба говорили про Ларьку, про Варьку, про Ларину жену | |
| На дворе трава, на траве дрова, не руби дрова на траве двора | |
| Рапортовал, да не дорапортовал, дорапортовывал, да зарапортовался | |
| Рыла свинья белорыла, тупорыла; полдвора рылом изрыла, вырыла, подрыла | |
| Съел молодец тридцать три пирога с пирогом, да все с творогом | |
| Тридцать три корабля лавировали, лавировали, да не вылавировали. | |
| Королева Клара строго карала Карла за кражу коралла. | |
| Всех скороговорок не перескороговоришь, не перевыскороговоришь. | |
| Была у Фрола, Фролу на Лавра наврала, пойду к Лавру, Лавру на Фрола навру. | |
| Маланья-болтунья молоко болтала, выбалтывала, не выболтала. | |
| На мели мы лениво налима ловили, на мели мы ловили линя. | |
| О любви не меня ли вы мило молили, и в туманы лимана манили меня? | |
| Стоит поп на копне, колпак на попе. Копна под попом, поп под колпаком. | |
| Наш голова вашего голову головой переголовил, перевыголовил. |
Практическая работа №6
Тема Расчет и построение кода Хаффмана.
Цель: Построение кодового «дерева» и вычисление коэффициента сжатия.
Теоретические сведения
Алгоритм Хаффмана – адаптивный алгоритм оптимального префиксного кодирования. Разработан в 1952 году аспирантом МТИ Дэвидом Хаффманом при написании курсовой работы. Идея алгоритма состоит в следующем: зная вероятность вхождения символов в сообщение, можно описать процедуру построения кодов переменной длинны, состоящих из целого количества битов. Символам с большей вероятностью присваиваются более короткие коды.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Символы входного алфавита образуют список свободных «узлов».
Таблица1. Список узлов по алфавиту
| Символ | A | B | C | D | E | F | |
| Число встречаемости |
Переставить таблицу по частоте встречаемости.
Таблица 2. Список узлов по частоте встречаемости
| Символ | C | E | B | F | A | D |
| Число встречаемости |
На основании таблицы строится дерево кодирования (H-дерево). Из последней таблицы берутся символы с наименьшей частотой (D и A).
30 10 5 10 20 25
C A D F B E
|__|
|
|15| Номер в рамке – сумма весов узлов D и A 10+5=15.
Снова берутся два символа с наименьшими частотами вхождения (F и новый узел).
30 10 5 10 20 25
C A D F B E
|__| |
| |
|15| |
|_ _|
|
|25| 10+15=25
Процесс продолжается пока все «дерево» не будет сформировано, т.е. не сведется к одному узлу.
30 10 5 10 20 25
C A D F B E
| |__| | | |
| | | | |
| |15| | | |
| |_ _| | |
| | | |
| |25| |45|
|_|55| _| |
|___|100|___|
Теперь когда «дерево» создано,можно кодировать файл.
Кодирование начинается с корня. Прослеживая вверх по дереву все повороты ветвей, присваиваем левому повороту 0-й бит, а правому -1-й бит.
Теперь к символу С необходимо сделать два левых поворота, следовательно символ С кодируется двух битовой последовательностью 00.К символу Е два правых поворота -11.Аналогично кодируются все остальные.
Таблица3. Кодовые последовательности
| Символ | A | B | C | D | E | F |
| Код |
Каждый символ изначально представлялся 8-мю битами(байт), и при уменьшении числа битов уменьшается и размер выходного файла.
Сжатие складывается таким образом(таблица4):
Таблица 4.Расчет сжатия символов
| Частота | первоначально | После уплотнения | Уменьшено на |
| С 30 | 30х8=240 | 30х2=60 | |
| А 10 | 10х8=80 | 10х3=30 | |
| D 5 | 5х8=40 | 5х4=20 | |
| F 10 | 10х8=80 | 10х4=40 | |
| B 20 | 20х8=160 | 20х2=40 | |
| E 25 | 25х8=200 | 25х2=50 |
Первоначальный размер файла: 100байт = 800бит
Размер сжатого файла: 30 байт = 240 бит
Процент сжатия: (240/800)х100% = 70%.
Порядок выполнения работы.
- Взять данные для расчета согласно варианта задания в приложении.
- Создать таблица списков узлов по алфавиту и встречаемости.
- Построить H-дерево.
- Заполнить таблицу кодовых последовательностей.
- Рассчитать сжатие символов.
- Рассчитать размер сжатого файла и процент сжатия.
Приложение. Варианты задания
| Номер варианта | Фраза для кодирования |
| Баркас приехал в порт Мадрас. Матрос принёс на борт матрас. В порту Мадрас матрас матроса порвали в драке альбатросы. | |
| Шли три попа, три Прокопья попа, три Прокопьевича, говорили про попа, про Прокопья попа, про Прокопьевича. | |
| Вашему пономарю нашего пономаря не перепономаривать стать: наш пономарь вашего пономаря перепономарит, перевыпономарит. | |
| Везет Сенька Саньку с Сонькой на санках. Санки скок, Сеньку с ног, Соньку в лоб, все в сугроб.. | |
| Ехал Гpека чеpез pеку, видит Гpека в pеке - pак. Сунул Гpека pуку в pеку, pак за pуку Гpеку - цап! | |
| Говорил попугай попугаю:"Я тебя, попугай, попугаю".Отвечает ему попугай:"Попугай, попугай, попугай!" | |
| Говорили про Прокоповича. Про какого про Прокоповича? Про Прокоповича, про Прокоповича, про Прокоповича, про твоего. | |
| Дворник дверь два дня держал, деревянный дом дрожал. Ветер дёргал в доме дверь, дворник думал – это зверь. | |
| Ежик в бане вымыл ушки,шею, кожицу на бpюшке. А на встpечу ему волк,на ежа зубами - щелк. Еж иголки показал,волк со стpаху убежал. | |
| Здорово, отеч, братеч, сестрича, приятель, друг, – скажи челобитье поклон: прости, отеч, мать, дедка, батюшка, братеч, сестрича, птича, курича.. | |
| И при Прокопе кипит укроп, И без Прокопа кипит укроп; И ушёл Прокоп – кипит укроп, И пришёл Прокоп – кипит укроп. | |
| На дворе трава, на траве – дрова, дрова вдоль двора, дрова вширь двора, не вместит двор дров, дрова надо выдворить. | |
| Ужа ужалила ужица. Ужу с ужицей не ужиться. Уж от ужаса стал уже - ужа ужица съест на ужин и скажет: (начинай сначала). | |
| На мели мы налима лениво ловили, Меняли налима вы мне на линя. О любви не меня ли вы мило молили, И в туманы лимана манили меня? | |
| Худ едет на гору, худ едет под гору; худ худу бает: ты худ, я худ; сядь худ на худ; погоняй худ худом, железным прутом. |
Контрольные вопросы
- Опишите алгоритм сжатия.
- Как посчитать коэффициент сжатия
- В каком случае сжатие больше.
- Что такое H-дерево.
Практическая работа №7
Тема: Сжатие информации по алгоритму Хэмминга.
Цель: Научиться кодированию тестового слова по алгоритму Хэмминга.
Теоретические сведения
Ричард Хэмминг на протяжении нескольких лет проводил много времени над построением эффективных алгоритмов исправления ошибок. В 1950 г он опубликовал способ, который известен как код Хэмминга(КХ).
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение.
КХ состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Пример работы
Подготовка
Пусть у нас есть сообщение «АвтД», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи КХ.
1. Представим слово в бинарном виде. Любое слово кодируется через таблицу кодов ASCII. ASCII (англ. A merican s tandard c ode for i nformation i nterchange) — название таблицы (кодировки, набора), в которой некоторым распространённым печатным и непечатным символам сопоставлены числовые коды.
Таблица ASCII
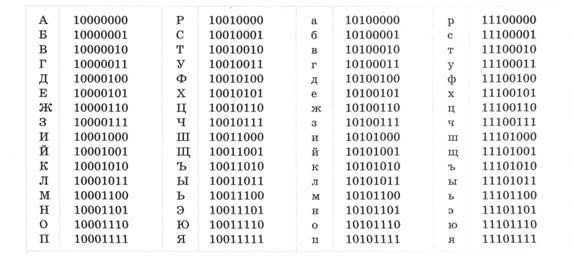
Преобразование сообщения в цифровой код
| Символ | Код ASCII | Бинарное число |
| А | ||
| в | ||
| т | ||
| Д |
2. На этом этапе определяются с длиной информационного слова, то есть длиной строки из нулей и единиц, которые будем кодировать. Допустим, длина слова будет равна 16. Таким образом, необходимо разделить исходное сообщение («АвтД») на блоки по 16 бит, которые потом кодируют отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, получены две бинарные строки по 16 бит:
Ав тД
1000000010100010 1110001010000100
3. После этого процесс кодирования распараллеливается, и две части сообщения («Ав» и «тД») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, получилось 5 контрольных бит (выделены жирным):
Ав тД
00 1 0 000 0 0000101 0 00010 00 1 0 110 0 0010100 0 00100
Таким образом, длина всего сообщения увеличилась на 5 бит. Всего 21. До вычисления самих контрольных бит, присвоим им значение «0».