и совершенствование математической модели

на экспоненциальной регрессии

2.3.1. Выделить 2 ячейки и открыть статистическую функцию ЛГРФПРИБЛ (рис. 7), сходную с функцией ЛИНЕЙН, но в отличие от последней рассчитывающую коэффициенты b и m экспоненциальной кривой y = b(m^x) [5, 6].

 

Рис. 7. Аргументы функции ЛГРФПРИБЛ

2.3.2. Ввести в качестве аргументов:

- «Известные значения x»;

- точно соответствующие им «Известные значения у»;

- в «Конст» - логическое значение ИСТИНА (любое ненулевое число) либо оставить незаполненным. (Если «Конст» имеет значение ЛОЖЬ, то значение m подбирается так, чтобы выполнялось b = 1.)

- в «Статистика» - логическое значение «ЛОЖЬ» (0 или отсутствует какое-либо значение), которое указывает, что дополнительные статистические данные по регрессии не требуются и функция ЛГРФПРИБЛ подсчитает только коэффициенты регрессии.

Примечания:

А. Если в качестве аргумента «Статистика» представлено любое другое число («ИСТИНА»), то производится расчёт дополнительной статистики, структура которой полностью соответствует структуре, выводимой в этом случае функцией ЛИНЕЙН (см. табл. 1).

Б. Поскольку инструмента анализа, сходного с инструментом «Регрессия», но «работающего» с экспоненциальной зависимостью в программе MS Excel не предусмотрено, в данном случае результаты дополнительной статистики являются единственными в своём роде. Поэтому хоть и не обозначенные подробно, они могут быть очень полезны.

2.3.2. Набрать комбинацию клавиш CTRL+SHIFT+ENTER, в результате чего в первой ячейке будет выведен коэффициент b, а во второй ячейке - коэффициент m уравнения y = b(m^x). (При нажатии «ОК» будет подсчитан только коэффициент b). Отразить результаты в таблице MS Excel.

2.3.3. Открыть статистическую функцию РОСТ (рис. 8), рассчитывающую значения y для новых значений x, то есть сходную с функциями ПРЕДСКАЗ и ТЕНДЕНЦИЯ, см. выше, но применительно не к линейной, а к экспоненциальной зависимости.

 

Рис. 8. Аргументы функции РОСТ

 

2.3.4. Рассчитать значение функции РОСТ, введя в качестве аргумента («Новые значения x») величину x, равную удвоенному максимальному известному значению x, и сравнить с аналогичным значением, рассчитанным с помощью функции ТЕНДЕНЦИЯ и ПРЕДСКАЗ (см. п.п. 2.2.6, 2.2.8).

 

 

2.4. Графические опции, предназначенные для анализа

регрессионной модели

2.4.1. Построение регрессионной зависимости и освоение способов её аппроксимации

2.4.1.1. Открыть «Мастер диаграмм» программы MS Excel, предварительно выделив массив ячеек, определяющий рассматриваемую зависимость (величина, определяющая аргумент x функции должна располагаться в первом слева столбце или в первой сверху строке массива).

2.4.1.2. Выбрать «Точечную» диаграмму без соединяющих линий и нажать «просмотр результата», чтобы убедиться, что аргумент x функции располагается по оси абсцисс, а значения функции – по оси ординат.

2.4.1.3. Нажимая «Далее» и выполняя предлагаемые действия, получить корреляционный график случайной функции , каждая точка которого изображает пару пере­менных x и y.

2.4.1.4. Используя опции «Формат оси», «Формат области построения» добиться наибольшей наглядности полученного графика и скопировать его (сделать пять расположенных рядом копий).

2.4.1.5. Для нанесения на график линии, которая на основе метода наименьших квадратов (МНК) аппроксимирует точки корреляционного графика, нажать правой кнопкой мыши на одну из точек, выбрать «Добавить линию тренда» (рис. 9).

2.4.1.6. Поставить «галочки» на опциях «показывать уравнение на диаграмме» и «поместить на диаграмму величину достоверности аппроксимации» (коэффициент детерминации R²).

 

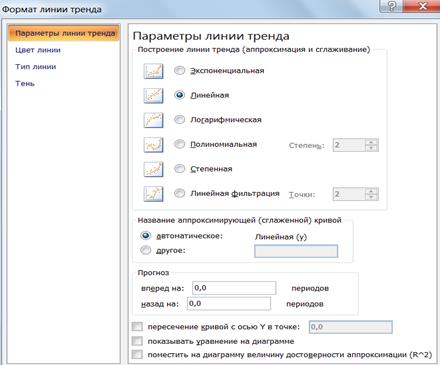
Рис. 9. Опции параметров линии тренда

 

2.4.2. Выбор вида аппроксимирующей функции

 

2.4.2.1. Повторить п.п.2.4.1.5 - 2.4.1.6 для различных графиков и выбрать последовательно экспоненциальную, линейную, логарифмическую, степенную и полиномиальную 6-й степени линии тренда. Поставить галочку на «поместить на диаграмму величину достоверности аппроксимации».

2.4.2.2. Выбрать способ, оптимальный с точки зрения точности аппроксимации экспериментальных данных, который обеспечивает максимальную величину коэффициента детерминации R². (Кроме точности аппроксимации в практике выбора способа аппроксимации следует руководствоваться теоретическими представлениями о физической связи рассматриваемых СВ, а также здравым смыслом, основанным на соображении, что эта связь не должна быть слишком сложной).

 

2.4.3. Анализ влияния вида аппроксимирующей функции

(степени полинома) на точность аппроксимации

Примечание. Разумеется, выбор функции, наиболее точно аппроксимирующей связь между характеристикой y и факторами X_i, определяется расположением экспериментальных точек, соответствием этого расположения теоретическому закону, см. § 5.1. Задача этой части работы показать, что при аппроксимации экспериментальных данных полиномом наблюдается тенденция: с увеличением степени полинома точность аппроксимации увеличивается.

2.4.3.1. Для построенного по п. 2.4.1 корреляционного графика по точкам, представляющим собой пары значений (x_i, y_i), построить линии тренда:

- линейную (полином первой степени);

- полиномиальные всех возможных степеней от 2 до 6.

2.4.3.2. Для каждой линии тренда определить характеристику точности аппроксимации - коэффициент детерминации R² (вкладка «Параметры», см. рис. 9).

2.4.3.3. Построить таблицу, в первой графе которой указана степень полинома (от 1 до 6), а во второй графе - соответствующее значение R².

2.4.3.4. Построить график зависимости коэффициента детерминации R² от степени полинома, которым аппроксимируется "корреляционный график".

2.4.3.5. Сделать заключение о влиянии степени полинома на коэффициент детерминации R².

 

2.5. Определение коэффициентов уравнения регрессии

с помощью надстройки Excel «Поиск решения»

 

Определение коэффициентов уравнения регрессии можно представить как оптимизационный процесс по минимизации целевой функции методом линейного программирования. Надстройка «Поиск решения» позволяет итерационным методом определить коэффициенты любого уравнения регрессии, если в качестве целевой функции выбрать сумму квадратов остатков. Под остатком понимается разность между фактическим и расчетным значением зависимой переменной. Данный метод определения коэффициентов уравнения регрессии называют методом наименьших квадратов. Окно надстройки «Поиск решения» показано на рисунке 10.

 

Рис. 10. Окно надстройки "Поиск решения"

Надстройка "Поиск решения" работает с группой ячеек:

· ячейками переменных решения, которые используются при расчете формул в целевых ячейках;

· ячейками ограничения.

Надстройка "Поиск решения" изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит результат в целевой ячейке.

Для знакомства введите в таблицу значения фактора Х (столбик А) и значения отклика Y (столбик В), как показано на рисунке 11.

Назначьте ячейки В14 и В15 соответственно для коэффициентов и уравнения линейной регрессии Y= 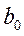+ X.

Первоначально в этих ячейках значения должны отсутствовать. В дальнейшем в них будет занесен результат выполнения программы «Поиск решения».

В диапазон ячеек С2:С11 введите результат расчетов по формуле Y= + X. В качестве значений и необходимо взять значения ячеек соответственно В14 и В15, значения X надо последовательно выбирать из массива А2:А11. Например, в ячейке С2 должна быть введена следующая формула = $В$14 + $В$15*А2, в ячейке СЗ должна быть введена формула = $В$14 + $В$15*А3 и т. д.

Введите в массив ячеек D2:D11 квадраты отклонений (е²). Квадраты отклонений вычисляются по формуле . Например, в ячейке D2 должна быть введена следующая формула: = (В2 - C2)^2.

В ячейку С17 введите целевую функцию, которая будет равна сумме квадратов отклонений, т. е. сумма ячеек массива D2:D11. Например, в ячейке С17 должна быть введена формула:

= D2 + D3 + D4 + D5 + D6 + D7 + D8 + D9 + D10 + D11..

Все подготовительные операции произведены, теперь необходимо так изменять численные значения и , чтобы значение целевой функции было минимальным. Эту процедуру выполнит программа «Поиск решения».

Откройте программу «Поиск решения», заполните параметры программы в соответствии с рисунком 11. Нажмите кнопку «Выполнить» и получите результат, представленный на рисунке 12.

Рис. 11. Параметры программы «Поиск решения»

 

 

№	X	Y	Y расчётное	квадрат остатка
			13,08333112	1,173606316
			13,66666499	1,777782257
			14,83333272	3,361108864
			14,83333272	1,361112541
			16,00000045	0,999999092
			17,16666819	0,694441909
			18,33333592	5,444456522
			18,91666979	0,006943924
			20,08333752	0,006945143
			20,08333752	0,840270099
коэффициенты		Целевая функция:	15,66666667
B0	11,9167
B1	0,58333

Рис. 12 Результат расчета коэффициентов линейной модели с помощью программы «Поиск решения»

Значения коэффициентов уравнения регрессии и находятся в ячейках B14 и B15 соответственно.

3. Многофакторный регрессионный анализ

3.1. Анализ и оценка достоверности модели в рамках

инструмента «Регрессия»

3.1.1. Открыть файл MS Excel «многофакторный регрессионный анализ» с таблицей исходных данных для 140 оставшихся при выполнении Вами п. 1.5.4. экспериментальных точек.

3.1.2. Открыть инструмент анализа данных «Регрессия» (рис. 2), позволяющий применительно к многофакторному анализу получить коэффициенты b₀ и b_i уравнения линейной регрессии, описывающего зависимость контролируемой величины отклика Y от выбранных факторов X_i:

Y = b₀+ Σ b_i X _i, (3)

3.1.3. Ввести во «Входной интервал x» столбцы значений X_i, а во «Входной интервал y» - столбец соответствующих значений отклика y (см. 2.1.1.3) и нажать ОК, получив 3 таблицы, сходные с представленными в сводной табл. 2.

Таблица 2. Результаты линейного регрессионного анализа влияния пяти факторов на характеристику качества

Регрессионная статистика
Множественный R	0,63
R-квадрат	0,4
Нормированный R-квадрат	0,38
Стандартная ошибка	1,02
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		93,8	18,8	18,03048	1,08E-13
Остаток		141,5	1,04
Итого		235,3
	Коэффициенты	Стандартная ошибка	t- статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	4,27	3,51	1,22	0,23	-2,7	11,2
H	0,436	2,37	0,18	0,85	-4,25	5,12
K	-0,029	0,26	-0,11	0,91	-0,55	0,49
Μ	-0,012	0,006	-1,89	0,06	-0,0242	0,0005
Pb	-0,064	0,029	-2,24	0,03	-0,121	-0,008
Si	0,0057	0,0007	7,63	3,6E-12	0,004	0,007

3.1.4. Оценить достоверность полученной модели по величине коэффициента детерминации «R-квадрат» в «Регрессионной статистике» и по результатам многофакторного дисперсионного анализа, основываясь на следующих принципах:

- сравнении составляющих дисперсии, приходящихся на одну степень свободы (MS), по варьируемым факторам вместе («Регрессия») и по всем остальным случайным и не учитываемым факторам («Остаток»). Чем больше первая составляющая превышает вторую (то есть чем больше расчётный критерий Фишера F), тем выше достоверность полученной модели;

- сравнении расчётного F- значения уровня значимости «Значимость F» с принятым в данной отрасли уровнем значимости α (0,05). (Если «Значимость F» < α, это говорит о достаточно высокой достоверности (более 95%) получаемой регрессионной модели.)

3.1.5. Сделать заключение о наличии или об отсутствии необходимости совершенствования полученной модели.

 

3.2. Оценка значимости коэффициентов регрессии

и совершенствование математической модели

3.2.1. Оценить значимость каждого коэффициента регрессии, основываясь на принципах, описанных для однофакторной модели, см. п. 2.1.1.4, сравнивая величину «P-Значения» с принятым уровнем значимости α и сравнивая расчётные значения коэффициентов Стьюдента с их «критическим» (табличным) значением.

3.2.2. Исключить из анализируемых данных факторы (столбцы данных, им соответствующие), которые характеризуются самыми малозначимыми коэффициентами регрессии.

3.2.3. Повторить для оставшихся (двух или трёх) факторов многофакторный регрессионный анализ, см. п. 3.1.2.

3.2.4. Оценить достоверность вновь полученной модели, основываясь на принципах, описанных для однофакторной модели, см. п. 3.1.3.

3.2.5. Оценить значимость вновь полученных коэффициентов регрессии, основываясь на принципах, описанных для однофакторной модели, см. п. 3.2.1.

3.2.6. Сделать заключения об эффективности совершенствования математической модели и многофакторного регрессионного анализа в целом.

 

3.3. Статистические функции MS Еxcel, предназначенные для многофакторного регрессионного анализа

3.3.1. Выделить в таблице файла «многофакторный регрессионный анализ» массив из расположенных рядом не менее пяти строк и не менее шести столбцов и открыть статистическую функцию ЛИНЕЙН (см. рис. 3), рассчитывающую коэффициенты линейного уравнения (3).

3.3.2. Ввести в качестве аргументов:

- «Известные значения x» - значения выбранных Вами в п. 3.2 значимых факторов, 140 точек;

- «Известные значения у» - 140 соответствующих точек;

- «Конст» - логическое значение ИСТИНА (любое ненулевое значение) или пропустить;

- «Статистика» - логическое значение ИСТИНА (любое ненулевое число).

3.3.3. Набрать комбинацию клавиш CTRL+SHIFT+ENTER, в результате чего в порядке, представленном в табл. 1, будут выведены коэффициенты регрессии и регрессионной статистики.

3.3.4. Проверить соответствие полученных коэффициентов регрессии и регрессионной статистики результатам, рассчитанным с использованием инструмента «Регрессия», п. 3.1.2.

3.3.5. Открыть функцию «ТЕНДЕНЦИЯ» (см. рис. 4), которая для заданного массива новых значений x определяет значения y в соответствии с линейным трендом, рассчитанным для массивов известных значений y и известных значений x.

3.3.6. Рассчитать значения функции ТЕНДЕНЦИЯ, введя следующие аргументы:

- «Известные значения x» (значения всех существенных факторов);

- «Известные значения у»;

- «Новые значения x» - для каждого существенного фактора x_i, равные удвоенному и утроенному значению максимального известного значения x_i;

- «Конст» - любое ненулевое число.

3.3.7. Выделить в одной строке (n + 1) расположенных рядом ячеек, где n - количество существенных факторов, и открыть статистическую функцию ЛГРФПРИБЛ (см. рис. 7), сходную с функцией ЛИНЕЙН, см. выше, но применительно к экспоненциальной зависимости.

3.3.8. Ввести в качестве аргументов:

- «Известные значения x_i»;

- «Известные значения у»;

- «Конст» - логическое значение ИСТИНА (любое ненулевое число) либо оставить незаполненным;

- «Статистика» - логическое значение «ЛОЖЬ» (0 или отсутствует какое-либо значение).

3.3.9. Набрать комбинацию клавиш CTRL+SHIFT+ENTER, в результате чего в первой ячейке будет выведен свободный член, а во второй и в последующих ячейках – коэффициенты регрессии для каждого рассматриваемого фактора.

3.3.10. Открыть статистическую функцию РОСТ (см. рис. 8), сходную с функцией ТЕНДЕНЦИЯ, см. выше, но применительно к экспоненциальной зависимости.

3.3.11. Рассчитать значения функции РОСТ, введя в качестве аргумента «Новые значения x» для каждого существенного фактора x_i, равные удвоенному и утроенному значению максимального известного значения x_i, и сравнить с аналогичными значениями, рассчитанными с помощью функции ТЕНДЕНЦИЯ, см. п. 3.3.6.

Библиографический список

1. Международный стандарт ISO 9001. Системы менеджмента качества. Требования. - Третье издание 2000-12-15. - ISO, 2000. - 41 с.

2. ГОСТ Р ИСО/ТО 10017-2005. Статистические методы. Руководство по применению в соответствии с ГОСТ Р ИСО 9001. - Дата введения 2005-07-01. - М.: Стандартинформ, 2005. - 19 с.

3. ГОСТ Р 50779.0-95. Статистические методы. Основные положения. - Дата введения 1996-07-01. - М.: Госстандарт России, 1995. - 12 с.

4. ГОСТ Р ИСО 11462-1 - 2007. Статистические методы. Руководство по внедрению статистического управления процессами. Часть 1. Элементы. - Дата введения - 2007-09-01. - М.: Стандартинформ, 2007. - 16 с.

5. Кувалдин, Ю.И. Исследование связи случайных величин в металлообработке с использованием программы MS EXCEL / Ю.И. Кувалдин, М.З. Певзнер. - Киров: Изд-во ВятГУ, 2011. - 66 с.

6. Кобзарь, А.И. Прикладная математическая статистика. Для инженеров и научных работников / А.И. Кобзарь. - М.: ФИЗМАТЛИТ, 2006. - 816 с.

7. Саймон, Д. Анализ данных в Excel: наглядный курс создания отчетов, диаграмм и сводных таблиц / Д. Саймон: пер. с англ. - М.: Издательский дом "Вильямс", 2004. - 528 с.

8. Макарова, Н.В. Статистика в Ехсеl / Н.В. Макарова, В.Я. Трофимец. - М.: Финансы и статистика, 2002. - 368 с.

9. Козлов, А.Ю. Статистические функции MS Excel в экономико-статистических расчётах / А.Ю. Козлов, В.С. Мхитарян, В.Ф. Шишов; под ред. В.С. Мхитаряна. - М.: ЮНИТИ-ДАНА, 2003. - 231 с.

10. Певзнер, М.З. Освоение инструментов анализа и статистических функций программы MS EXCEL на примерах решения задач предварительной обработки данных: учебное пособие / М.З. Певзнер, А.Я. Часников. - Киров: Изд-во ВятГУ, 2011. - 43 с.

 

 

Грачёв Сергей Павлович

Певзнер Михаил Зиновьевич

 

ПРИМЕНЕНИЕ ПРОГРАММЫMS EXCEL

ДЛЯ РЕГРЕССИОННОГО АНАЛИЗА

ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ

 

Учебно-методическое пособие

 

 

Подписано в печать.2014. Печать цифровая. Бумага для офисной техники.

Усл. печ. л. 1,5. Тираж 20. Заказ №.

 

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Вятский государственный университет»

610000, г. Киров, ул. Московская, 36, тел.: (8332) 64-23-56, https://vyatsu.ru