...


 yn y2 y1
yn y2 y1










 P P P
P P P
 |

 Рис. 4. Схема параллельного суммирования
Рис. 4. Схема параллельного суммирования
Тс(пар) @ ntлэ .
Очевидно, Tc(посл) ≤ Тс(пар), так как

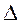 t @ (3,6) ktлэ,
t @ (3,6) ktлэ,
где k - коэффициент запаса, обеспечивающий полное окончание всех переходных процессов в сумматоре последовательного действия k Î [1,2, 1,3].
Недостатком такого параллельного суммирования является большое время распространения сигналов переноса Pi. Параллельные безрегистровые сумматоры обеспечивают наибольшую скорость суммирования, если снабжены схемой ускоренного переноса.
Сложение чисел с плавающей запятой
При сложении чисел складываемые цифры (разряды) должны иметь одинаковый вес. Это требование выполняется, если складываемые числа имеют одинаковые порядки. Пусть имеются два числа с плавающей запятой:
A=±mAr±pA,
B=±mBr±pB.
Алгоритм сложения чисел с произвольными знаками состоит в следующем.
1. Производится сравнение порядков pA и pB. Для этого из порядка числа A вычитается порядок числа B. Разность p=pA-pB указывает, на сколько разрядов требуется сдвинуть вправо мантиссу числа с меньшим порядком. Если p=pA-pB>0, то pA>pB и для выравнивания порядков необходимо сдвинуть вправо мантиссу MB. Если p=pA-pB<0, то pB>pA и для выравнивания порядков необходимо сдвинуть вправо мантиссу MA. Если p=pA-pB=0, то pA=pB и порядки слагаемых выравнивать не требуется.
2. Выполняется сдвиг соответствующей мантиссы до тех пор, пока p≠0.
3. Выполняется сложение мантисс MA и MB по правилу сложения правильных дробей.
4. Если при сложении мантисс произошло переполнение, то производится нормализация путем сдвига мантиссы суммы вместе со знаковым разрядом вправо на один разряд с увеличением порядка на единицу. Если же происходит денормализация, то выполняется сдвиг мантиссы результата на соответствующее количество разрядов в сторону, противоположную нарушению нормализации с соответствующим изменением порядка суммы.
Пример: МА=-0,10110 рА=+0111
МВ=-0,11011 рВ=+0101
[MA]доп=1,01010 p= [рА]доп+[-рВ]доп= 0.0111
[MB]доп=1,00101 + 1.1011
10.0010
Так как [рА-рВ]доп>0, то сдвигу подвергается мантисса МВ.
В рассматриваемом примере при каждом сдвиге мантиссы на один разряд из положительной разности порядков производим последовательное вычитание единицы до тех пор, пока в результате не будет получен ноль. При этом выполняется анализ разности порядков на каждом шаге. Если она отлична от нуля, то производится очередной сдвиг соответствующей мантиссы. В случае если разность [рА-рВ]доп<0, необходимо либо прибавлять единицу до нулевого результата, либо изменить знак разности на противоположный и, как и выше, выполнять вычитание единицы.
[MB]доп=1,00101 0.0010
[-1]доп= 1.1111
[MB]доп=1, 1 0010 1 0.0001
[MB]доп=1, 11 001 01 [-1]доп= 1.1111
0.0000
[MB]доп=1,11001 01
[MA]доп= 1,01010
11,00011 01 = [МА+В] рА+В=max(рА,pB)=pA=+0.0111
Полученный результат нормализован. После выполнения операции округления получим [МА+В]= 1,00011.
Машинные методы умножения чисел в прямых кодах
Операция умножения состоит из ряда последовательных сложений. Сложением управляют разряды множителя: если в очередном разряде множителя содержится единица, то к сумме добавляется множимое. При этом, в зависимости от метода умножения, выполняется сдвиг либо множимого, либо частичной суммы. Наряду с этим умножение можно начинать как с младших, так и со старших разрядов множителя. Для умножения используют модули сомножителей. Знак произведения определяется сложением по модулю 2 знаковых разрядов сомножителей.
Введем некоторые обозначения, используемые ниже: 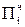 - частичное произведение,
- частичное произведение,  - частичная сумма.
- частичная сумма.
Ниже приводится схема четырех алгоритмов умножения (рис. 5).

Остановимся более подробно на реализации умножения согласно алгоритму А.
Представим Мн = А = 0,а1а2…аn
Мт = B = 0,b1b2….bn = b12-1+b22-2+…+bn2-n+bn2-n
Мн∙Мт = С=А∙В= 0,а1а2…аn (b12-1+b22-2+…+bn2-n) =
= 0+(b1∙0,а1а2…аn)2-1+…+(bn-1∙0,а1а2…аn)2-(n-1)+(bn∙0,а1а2…аn)2-n =
= 0+b1∙A2-1+…+bn-1∙A2-(n-1)+…+bn∙A2-n = 0+bn∙A2-n+bn-1∙A2-(n-1)+…+b1∙A2-1 =
= (…((0+bn∙A)2-1+bn-1∙A)2-1+…+b1∙A)2-1
Ниже приведены (без вывода) остальные три реализации алгоритмов (Б, В и Г) умножения.
Мн∙Мт = С=А∙В = 0+bn∙A+bn-1∙A∙22+…+b1∙A∙2n-1 (алгоритм Б)
Мн∙Мт = С=А∙В = (…(0+b1∙A) ∙21+b2∙A)∙21+…+bn∙A) (алгоритм В)
Мн∙Мт = С=А∙В = 0+b1∙A∙2-1+b2∙A∙2-2+…+bn∙A∙2-n (алгоритм Г)
Структурные схемы операционных устройств, выполняющих умножение по алгоритмам А, Б, В и Г, приведены на рис 6.
Рассмотрим пример умножения чисел согласно алгоритму А.
Пример: Мн = 0,1011
|
0,0000 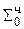 начальное содержимое сумматора
начальное содержимое сумматора
+ 0,1011  = Мн ∙ b4 первое частичное произведение
= Мн ∙ b4 первое частичное произведение
0,1011 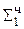 первая частичная сумма
первая частичная сумма
0, 0 101 1 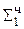 ∙ 2-1 сдвиг первой частичной суммы
∙ 2-1 сдвиг первой частичной суммы
+ 0,0000  = Мн ∙ b3 второе частичное произведение
= Мн ∙ b3 второе частичное произведение
0,0101 1 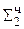 вторая частичная сумма
вторая частичная сумма
0, 0 010 11 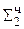 ∙ 2-1 сдвиг второй частичной суммы
∙ 2-1 сдвиг второй частичной суммы
+ 0,1011 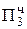 = Мн ∙ b2 третье частичное произведение
= Мн ∙ b2 третье частичное произведение
0,1101 11 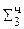 третья частичная сумма
третья частичная сумма
0, 0 110 111 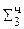 ∙ 2-1 сдвиг третьей частичной суммы
∙ 2-1 сдвиг третьей частичной суммы
+ 0,1011 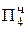 = Мн ∙ b1 четвертое частичное произведение
= Мн ∙ b1 четвертое частичное произведение
1,0001 111 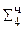 (возникло переполнение)
(возникло переполнение)
0, 1 000 1111 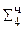 ∙ 2-1 сдвиг, получение верного результа-
∙ 2-1 сдвиг, получение верного результа-
та Мн∙Мт
Заметим, что при умножении чисел по алгоритму А на отдельных этапах операции возможно переполнение (попадание значащей единицы в знаковый разряд). Однако при последующем сдвиге переполнение устраняется. При использовании других алгоритмов (Б, В, Г) переполнения не возникает.

Время умножения чисел по алгоритму А tумн = (tсл + tсдв ) n, где n - число разрядов Мт. Следовательно, сдвиг и сложение нельзя выполнять в одном автоматном такте. Это наглядно показано на рис 7.

Ускорение операции умножения
Арифметические операции, к числу которых относится умножение, часто встречаются при решении задач на ЭВМ. Умножение является длинной операцией. Временные затраты на умножение чисел в прямых кодах можно оценить по формуле
 (3)
(3)
где pi – вероятность появления единицы в разрядах множителя, tсл – время формирования очередной частичной суммы, tсдв – время выполнения сдвига числа на один разряд.
Анализируя выражение (3), можно предложить различные пути сокращения величины Тумн: уменьшение времени на сдвиг, на формирование очередной суммы, уменьшение числа разрядов множителя. Этого можно достигнуть логическими или аппаратными методами. Рассмотрим логические методы ускорения умножения.
Один из наиболее простых способов состоит в том, чтобы при наличии нулевого разряда в множителе не выполнять формирование очередного (нулевого) частичного произведения, не изменяющего содержимое сумматора. В зависимости от используемого алгоритма умножения выполняется сдвиг либо частичной суммы, либо частичного произведения без выполнения суммирования.
Умножение с хранением переносов
Время, затрачиваемое на сложение двоичных чисел, состоит из времени, необходимого для поразрядного сложения, и времени на формирование переноса
tсл = tÅ + tпер.
Поразрядное сложение является элементарной операцией, и время на эту операцию может быть сокращено путем использования более быстродействующих элементов. В то же время если исключить необходимость выполнения межразрядных переносов при сложении, то время умножения уменьшится на tпер. Переносы, формируемые при сложении, записываются в отдельный регистр. Содержимое этого регистра добавляется в сумматор вместе с очередым частичным произведением. При этом сложение может выполняться паралельно по всем разрядам. На последнем такте (при умножении на последний разряд множителя) сложение выполняется с учетом межразрядных переносов. В заключение следует отметить, что этот метод используется с алгоритмом A.
Пример: Мн = 0,1011
Мт= 0,1101
0,0000 
0,0000 регистр переносов
 + 0,1011
+ 0,1011 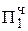 = Мн b4
= Мн b4
0,1011 
0,0000 регистр переносов
0, 0 101 1  2-1
2-1
 + 0,0000
+ 0,0000 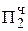 = Мн b3
= Мн b3
0,0101 1 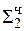
0,0000 регистр переносов
0, 0 010 11 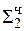 2-1
2-1
 + 0,1011
+ 0,1011  = Мн b2
= Мн b2
0,1001 11 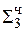
0,0010 регистр переносов
0, 0 100 111 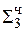 2-1
2-1
 + 0,1011
+ 0,1011 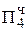 = Мн b1
= Мн b1
1,0001 111 
0, 1 000 1111  2-1
2-1
Умножение на два разряда множителя одновременно
Разбиение множителя на группы длиной k разрядов означает переход к новой системе счисления с основанием 2k. Если при этом удается сократить количество элементарных действий, выполняемых при умножении (сложение и сдвиги), то сокращается время умножения. Остановимся более подробно на умножении на два разряда множителя за один такт (k=2). Это связано с анализом пар разрядов множителя.
Возможны четыре случая сочетания разрядов множителя: 00, 01, 10, 11. Умножение на каждую из пар разрядов множителя должно выполняться за один такт автоматного времени, то есть в каждом такте умножения должно выполняться не более одного сложения. Рассмотрим умножение на эти пары на примере алгоритма А.
В случае пары 00 необходимо выполнить только сдвиг частичной суммы на два разряда - 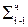 2-2.
2-2.
Для пары 01 выполняется добавление множимого в сумматор с последующим сдвигом суммы на два разряда - 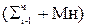 2-2.
2-2.
При наличии пары 10 возможны следующие варианты действий:
a) 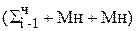 2-2, то есть в этом случае происходят два сложения, что противоречит требованию;
2-2, то есть в этом случае происходят два сложения, что противоречит требованию;
б)  2-2, в этом случае требуется дополнительный регистр для хранения удвоенного Мн;
2-2, в этом случае требуется дополнительный регистр для хранения удвоенного Мн;
в) 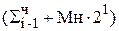 2-2, что соответствует добавлению к частичной сумме сдвинутого на один разряд влево множимого;
2-2, что соответствует добавлению к частичной сумме сдвинутого на один разряд влево множимого;
г)  2-1, то есть частичная сумма сдвигается на один разряд вправо до и после добавления к ней множимого.
2-1, то есть частичная сумма сдвигается на один разряд вправо до и после добавления к ней множимого.
При умножении на пару 11 (к частичной сумме необходимо добавить утроенное множимое) ее можно представить в виде
11 = (22 - 1)
Мн ∙ 11= Мн∙(22 - 1) = Мн∙22- Мн, то есть в текущем такте к частичной сумме добавляется множимое, взятое со знаком минус. Добавление Мн∙22 реализуется путем увеличения на единицу следующей старшей пары разрядов.
В табл.1 представлены правила преобразования множителя для системы (0,1,1).
Таблица 1
| Анализируемая пара разрядов Мт | Перенос из предыдущей пары | Преобразованная пара |
 11 11
| ||
 10 10
| ||
Пример: Мн = 0101
 Мт = 11000111
Мт = 11000111
 Мтп = 0101001001
Мтп = 0101001001
Умножение будем осуществлять согласно алгоритму А.
[- Мн]доп = 1.1011
2 Мн = 0.1010
0.0000 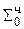
+ 1.1011  = -Mн
= -Mн
1.1011 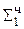
1. 11 10 11 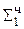 ∙ 2-2
∙ 2-2
+ 0.1010  = 2Mн
= 2Mн
0.1000 11 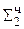
0. 00 10 0011 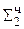 ∙ 2-2
∙ 2-2
0. 00 00 100011 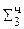 ∙ 2-2 (
∙ 2-2 (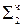 ∙ 2-4)
∙ 2-4)
+ 1.1011 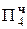 =-Mн
=-Mн
1.1011 100011 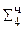
1. 11 10 11100011 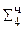 ∙ 2-2
∙ 2-2
+ 0.0101  = Mн
= Mн
0.0011 11100011 
0. 00 00 1111100011  ∙ 2-2
∙ 2-2
Время умножения на два разряда множителя одновременно
Появление любой из рассматриваемых пар множителей равновероятно. Следовательно, время умножения на два разряда множителя может быть выражено следующим соотношением: 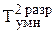 = (n/2 + 1) [0,75∙(tсл + tсдв) + (0,25∙tсдв], где n – количество разрядов множителя.
= (n/2 + 1) [0,75∙(tсл + tсдв) + (0,25∙tсдв], где n – количество разрядов множителя.
Умножение на четыре разряда одновременно
В этом случае с помощью приема, аналогичного приему, использованному в случае умножения на два разряда одновременно, можно рассматривать сразу тетраду двоичных разрядов. Может быть выведено общее правило сокращенного умножения:
1. Если цифра множителя bi-1 < r/2, то 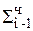 +
+  , где
, где  = Мн bi.
= Мн bi.
2. Если цифра множителя bi-1 ³ r/2, то 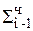 +
+ 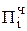 , где
, где  = [Мн (r - bi)]доп.
= [Мн (r - bi)]доп.
 Анализ четырех двоичных разрядов одновременно дает возможность осуществить сдвиг на четыре разряда за один такт.
Анализ четырех двоичных разрядов одновременно дает возможность осуществить сдвиг на четыре разряда за один такт.
Пример: Мн = 011
Мт = С49

 Мтп = 1457
Мтп = 1457
Можно заранее заготовить кратные множители: Мн, 2Мн, 4Мн, поместив их в дополнительные регистры. Это позволит сократить время, необходимое для формирования частичного произведения 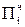 , равного от нуля до семи множимых.
, равного от нуля до семи множимых.
[+7Мн]доп = 0.10101 [+5Мн]доп= 0.01111 [+4Мн]доп= 0.01100
[-7Мн]доп = 1.01011 [-4Мн]доп = 1.10100
0.00000 
+ 1.01011  = -7Mн
= -7Mн
1.01011 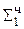
1. 1111 0 1011 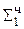 ∙ 2-4
∙ 2-4
+ 0.01111  = +5Mн
= +5Mн
0.01101 1011 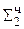
0. 0000 0 1101 1011 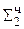 ∙ 2-4
∙ 2-4
+ 1.10100  =-4Mн
=-4Mн
1.10100 1101 1011 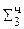
1. 1111 1 0100 1101 1011 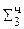 ∙ 2--4
∙ 2--4
+ 0.00011 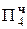 = +Mн
= +Mн
0.00010 0100 1101 1011 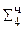
0. 0000 00010 0100 1101 1011 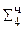 ∙ 2--4 = Мн∙Мт
∙ 2--4 = Мн∙Мт
Умножение в дополнительных кодах
Умножение чисел в дополнительных кодах может выполняться по любому из рассмотренных выше четырех алгоритмов, но отличается тем, что для получения верного результата необходимо вводить поправки. Умножение правильных дробей и целых чисел имеет некоторые различия.
Рассмотрим вначале умножение дробных чисел. Возможны четыре случая знакосочетания сомножителей.
1) Мн>0,
Мт>0.
В этом случае дополнительный код сомножителей совпадает с прямым кодом и умножение выполняется по правилам умножения в прямых кодах, в результате чего получается верный результат.
2) Мн>0,
Мт<0.
Так как Мн и Мт имеют разные знаки, то результат будет иметь отрицательный знак. Следовательно, результат должен быть представлен в дополнительном коде [Мн∙Мт]доп=2-Мн∙Мт. Для формирования произведения выполним умножение Мн на Мт¢ (дополнение):
Мн∙Мт¢= Мн ∙(1 - Мт)= Мн - Мн∙Мт.

 Таким образом, погрешность Δ умножения равна разности [Мн∙Мт]доп. и Мт∙Мн¢
Таким образом, погрешность Δ умножения равна разности [Мн∙Мт]доп. и Мт∙Мн¢
Δ=2-Мн∙Мт- Мн + Мн∙Мт=2-Мн=[-Мн]доп=[ [Мн]доп]доп
и должна быть внесена в полученный результат в качестве поправки.
Пример: Мн = 0,1011 (алгоритм умножения А)
Мт = - 0,1101
Δ= [- Мн]доп = 1,0101
[- Мт]доп = 1,0011
0,0000 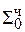
 + 0,1011
+ 0,1011 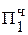 = Мн b4
= Мн b4
0,1011 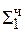
0, 0 101 1 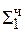 ∙ 2-1
∙ 2-1
+ 0,1011  = Мн b3
= Мн b3
 1,0000 1
1,0000 1 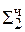 (произошло переполнение)
(произошло переполнение)
0 ,1 000 01 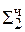 ∙ 2-1 (коррекция)
∙ 2-1 (коррекция)
0, 0 10 0001 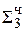 ∙ 2-1 (
∙ 2-1 (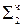 ∙ 2-1) ∙ 2-1
∙ 2-1) ∙ 2-1
0, 0 010 0001 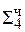 ∙ 2-1 ((
∙ 2-1 ((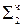 ∙ 2-1)∙ 2-1)∙ 2-1
∙ 2-1)∙ 2-1)∙ 2-1
+ 1,0101 Δ = [- Мн]доп (поправка)
 1,0111 0001
1,0111 0001 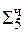 =[Mн ∙ Mт]доп
=[Mн ∙ Mт]доп
- 0,1000 1111 Mн ∙ Mт
В этом примере, а также в некоторых примерах, следующих ниже, происходит переполнение разрядной сетки, в результате которого искажаются и знаковая и значащая часть числа. Для коррекции (восстановления верного значения) производится немодифицированный сдвиг. В результате этого знаковый разряд сдвигается в значащую часть, а знаковый разряд меняет свое значение на противоположное.
3) Mн<0,
Mт>0.
Аналогично предыдущему случаю
[Мн∙Мт]доп=2-Мн∙Мт,
Мн¢∙Мт= (1 - Мн)∙Мт= Мт - Мн∙Мт.
Таким образом, погрешность умножения равна разности [Мн Мт]доп и Мт∙Мн¢.

 Δ=2-Мн∙Мт- Мт + Мн∙Мт=2-Мт=[-Мт]доп=[ [Мт]доп]доп.
Δ=2-Мн∙Мт- Мт + Мн∙Мт=2-Мт=[-Мт]доп=[ [Мт]доп]доп.
Использовать этот вариант неудобно, так как нужно вводить поправку [-Mт]доп в конце умножения, а в результате сдвигов Мт постепенно исчезает на регистре множителя и для поправки нужно либо вводить дополнительный регистр, либо вносить поправку в сумматор на первом такте умножения.
При этом знакосочетании возможно умножение без ввода поправки. Рассмотрим этот вариант на примере умножения по алгоритму Г (это справедливо и для других алгоритмов).
Мн∙Мт = А ∙ В = [ A ∙ b1∙ 2-1 ]доп + [ A ∙ b2∙ 2-2 ]доп+... + [A∙ bn∙ 2-n ]доп.
На основании теоремы, доказывающей что сумма дополнительных кодов есть дополнительный код суммы, получаем
[ A ∙ b1∙ 2-1 + A ∙ b2∙ 2-2 +... + A∙ bn∙ 2-n ]доп = [Мн ∙Мт]доп.
В этом случае поправка вводится автоматически на каждом этапе умножения.
Пример: Mн = -0,1011
Mт = 0,1101
|
0,00000000 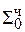
+ 1, 1 0101000  = [Mн ∙ b1 ∙ 2-1]доп
= [Mн ∙ b1 ∙ 2-1]доп
 1,10101000
1,10101000 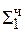
+ 1, 11 010100  = [Mн ∙ b2 ∙ 2-2]доп
= [Mн ∙ b2 ∙ 2-2]доп
 1,01111100
1,01111100 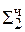
 + 1, 1111 0101
+ 1, 1111 0101 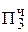 = [Mн ∙ b4 ∙ 2-4]доп
= [Mн ∙ b4 ∙ 2-4]доп
1,01110001 [Mн ∙ Mт]доп
-0,10001111 Mн ∙ Mт
4) Mн<0,
Mт<0.
Mн ∙ Mт = 2 - [Mн ∙ Mт]доп
[Mн]доп ∙ (1 - Mт) = [Mн]доп - [Mн]доп ∙ Mт = [Mн]доп - [Mн ∙ Mт]доп

 Δ=2 - [Mн ∙ Mт]gдоп - [Mн]доп + [Mн ∙ Mт]доп = 2 - [Mн]доп = [[Mн]доп]доп
Δ=2 - [Mн ∙ Mт]gдоп - [Mн]доп + [Mн ∙ Mт]доп = 2 - [Mн]доп = [[Mн]доп]доп
Пример: Mн = - 0,1011 умножение будем выполнять
Mт = - 0,1101 по алгоритму умножения Г
[Mн]доп = 1,0101
[Mт]доп = 1,0011
Δ =[-Mн]доп = 0,1011
0,00000000 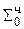
+ 1, 111 01010  = [Mн ∙ b3 ∙ 2-3]доп
= [Mн ∙ b3 ∙ 2-3]доп
 1,11101010
1,11101010 
+ 1, 1111 0101 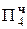 = [Mн ∙ b4 ∙ 2-4]доп
= [Mн ∙ b4 ∙ 2-4]доп

1,11011111 
 + 0, 1011 0000 Δ (поправка)
+ 0, 1011 0000 Δ (поправка)
0,10001111 [Mн∙ Mт]доп
Далее коротко остановимся на умножении целых чисел. При представлении целых чисел в дополнительном коде знаковый разряд входит в число n разрядов. Следовательно, при умножении целых чисел (в отличие от дробных) в дополнительных кодах знаковый разряд участвует в умножении наряду со значащими. То есть умножение ведется на [Mт]доп , а не на Мт ¢.
1) Mн > 0,
Mт > 0.
Как отмечалось выше, в этом случае умножение выполняется по правилам умножения чисел в прямых кодах.
2) Мн>0,
Mт<0,
[Мт]доп = 2n – Мт.

 Так как сомножители имеют разные знаки, то произведение Мн∙Мт<0, следовательно, [Mн∙Мт]доп=22n - Mн∙Мт. Однако при умножении Мн∙[Мт]доп получается Mн ∙(2n-Mт) =2n Mн - Mн∙Мт. Следовательно, погрешность в этом случае равна Δ = 22n–Mн∙Мт–2n Mн+Mн∙Мт = 22n–2n Mн = [–Мн]доп∙22n = [ [Мн]доп]доп∙22n.
Так как сомножители имеют разные знаки, то произведение Мн∙Мт<0, следовательно, [Mн∙Мт]доп=22n - Mн∙Мт. Однако при умножении Мн∙[Мт]доп получается Mн ∙(2n-Mт) =2n Mн - Mн∙Мт. Следовательно, погрешность в этом случае равна Δ = 22n–Mн∙Мт–2n Mн+Mн∙Мт = 22n–2n Mн = [–Мн]доп∙22n = [ [Мн]доп]доп∙22n.
Пример: Mн = +110
Mт = -101
[Mн]доп = 0.110
[Mт]доп = 1.011
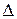 = [- Mн]доп = 1.010
= [- Mн]доп = 1.010
0.000 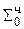
+ 0.110  = Mн∙b4
= Mн∙b4
0.110 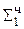
0. 0 11 0  ∙2-1
∙2-1
+ 0.110  = Mн∙b3
= Mн∙b3
1.001 0 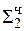 (возникло переполнение)
(возникло переполнение)
0. 1 00 10 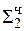 ∙2-1 (коррекция)
∙2-1 (коррекция)
0. 01 0 010 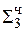 ∙2-1
∙2-1
+ 0.110 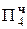 = Mн∙b1
= Mн∙b1
1.000 010  (возникло переполнение)
(возникло переполнение)
0. 1 00 0010  ∙2-1 (коррекция)
∙2-1 (коррекция)
+ 1.010 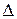 (поправка)
(поправка)
1.110 0010 [Mн×Mт]доп
- 001 1110 Mн×Mт
3) Мн<0,
Мт>0.
Здесь, как и при умножении дробных чисел, возможны два случая:
a) с вводом поправки в получаемое произведение
[Мн]доп = 2n – Mн.
Как и ранее, требуется получить [Мн∙Мт]доп= 22n - Мн∙Мт. Получаем
(2n - Мн) ∙ Мт = 2n ∙ Мт - Мн∙Мт.


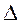 = 22n - Мн∙Мт - 2n ∙ Мт + Мн∙Мт = 2n(2n - Мт) = [-Мт]доп ∙ 2n;
= 22n - Мн∙Мт - 2n ∙ Мт + Мн∙Мт = 2n(2n - Мт) = [-Мт]доп ∙ 2n;
б) вариант без ввода поправки рассмотрим применительно к алгоритму умножения Г (как и ранее это справедливо и для других алгоритмов):
Mн∙Mт = A∙B = [A ∙ b1 ∙ 2-1 ]доп + [A ∙ b2 ∙ 2 -2]доп+- ... + [A ∙ bn ∙ 2-n]доп=
=[A ∙ b1 ∙ 2-1 + A ∙ b2 ∙ 2 –2 +- ... + A ∙ bn ∙ 2-n]доп=[Мн∙Мт]доп.
Пример: Мн = -110 Мт = 101 [Мн]доп = 1.010
[Мт]доп = 0.101
b1 ... b4
0.0000000 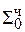
+ 0. 0 000000  = [MH ∙ b1]доп ∙ 2-1
= [MH ∙ b1]доп ∙ 2-1
0.0000000 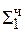
+ 1. 11 01000 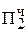 = [MH ∙ b2]доп ∙ 2-2
= [MH ∙ b2]доп ∙ 2-2
1.1101000 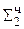
+ 1. 1111 010 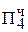 = [MH ∙ b4]доп ∙ 2-4
= [MH ∙ b4]доп ∙ 2-4
1.1100010 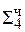
4) Mн < 0
Mт < 0
При этом сочетании знаков сомножителей в результате должно быть получено:
[Mн]доп = 2n – Mн,
[Mт]доп = 2n – Mт,
Mн ∙Mт = 22n - [Mн Mт]доп.
При умножении [Mн]доп∙[Mн]доп получается:
[Mн]доп∙[Mн]д =[Mн]доп (2n - Mт) = 2n [Mн]доп - 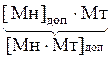
Пример: Мн = -110
Mт = -101
[Mн]доп = 1.010
[Mт]доп = 1. 011
b1 ... b4
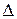 = [[Mн]доп]доп= 0.110
= [[Mн]доп]доп= 0.110
При умножении используем алгоритм Г.
0.0000000 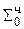
1. 1 010000  = [Mн∙b1]доп∙2-1
= [Mн∙b1]доп∙2-1
1.1010000 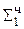
1. 111 0100  = [Mн∙b3] доп∙2-3
= [Mн∙b3] доп∙2-3
1.1000100 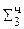
1. 1111 010  = [Mн∙b4] доп∙2-4
= [Mн∙b4] доп∙2-4
1.0111110 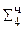
0.110 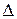 (поправка)
(поправка)
0.0011110 Mн Mт
Умножение на два разряда множителя в дополнительных кодах
| i | i+1 | i | i+1 |
| +4Mн | -Mн | +4Mн | -2Mн |
В отличие от умножения в прямых кодах преобразованию подвергается не только пара 11, но также и пара 10. Это позволяет упростить анализ кода и формирование преобразованного множителя.
В табл. 2 приведены преобразования i и i+1 пары множителя.
Таблица 2
| i-я пара | i+1-я пара | Преобраз. пара | Алгоритм | ||||
| х | y | z | - | x¢ | y¢ | A | Г |
| - | |||||||
| - | |||||||
| - | |||||||
| - | |||||||
 1 1
| - | ||||||
 1 1
| - | ||||||
 1 1
| - | ||||||
| - |
Действия, осущестляемые при выполнении, например, алгоритмов А и Г следующие:
(1) 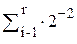 (6)
(6) 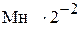
(2)  (7)
(7) 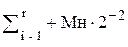
(3)  (8)
(8) 
(4) 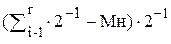 (9)
(9) 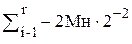
(5) 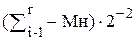 (10)
(10) 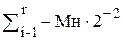
Если i+1 пара имеет старшую цифру 1, то умножение на эту пару будет соответствовать вычитанию одного или двух множителей. На рис. 9 приведена логическая схема для формирования сигнала выполняемого действия при анализе пары (xy) и старшего разряда (z) предыдущей пары при умножении чисел согласно алгоритму Г.
Как было показано выше, при умножении чисел в дополнительных кодах в общем случае необходимо вводить поправку для получения верного произведения. Однако при умножении на два разряда множителя этого выполнять не требуется. Если на умножение поступает отрицательный множитель, то при преобразовании его старшей пары происходит формирование дополнительной пары:
Мт = -10110
 [Мт]доп= 1.0 10 10
[Мт]доп= 1.0 10 10


 [Мт]допп= 01 01 01 10
[Мт]допп= 01 01 01 10
 При умножении на дополнительную пару (01) происходит вычитание одного множителя, а затем он должен быть добавлен в качестве поправки. Таким образом, тратится два такта на выполнение взаимоисключающих операций.
При умножении на дополнительную пару (01) происходит вычитание одного множителя, а затем он должен быть добавлен в качестве поправки. Таким образом, тратится два такта на выполнение взаимоисключающих операций.
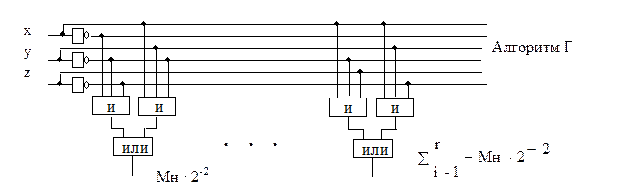
Рис. 9. Логическая схема формирования сигнала выполняемого действия
Пример:
Мн = + 0101 умножение выполним согласно
Mт = + 1100111 алгоритму Г
[Mн]доп = 0.0101
[Mт]доп = 0.1 10 01 11
Анализ пар Мт можно производить начиная от старших (при умножении по алгоритмам В и Г) и от младших разрядов (алгоритмы А и Б).

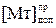
 = 10 10 10 01
= 10 10 10 01
[-2Mн]доп = 1.0110 [2Mн]доп = 0.1010
0.0000 00000000 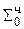
+ 0. 00 10 10000000  = 2MH∙2-2
= 2MH∙2-2
0.0010 10000000 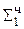
+ 1. 1111 01100000  = -2MH∙2-4
= -2MH∙2-4
0.0001 11100000 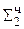
+ 0. 0000 00 101000  = 2MH∙2-6
= 2MH∙2-6
0.0010 00001000 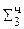
+ 1. 1111 1111 1011 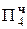 = -MH∙2-8
= -MH∙2-8
0.0010 00000011 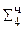 = [Mн Mт]доп
= [Mн Mт]доп
Пример:
Mн= - 0101 умножение выполним согласно
Mт = -1100111 алгоритму Б
[Mн]доп = 1.1011
[Mт]доп = 1.0 01 10 01


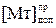 = 1.0 10 10 01
= 1.0 10 10 01
[2Mн]доп = 1.0110 [-2Mн]доп = 0.1010
0.000000 0000 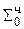
+ 1.111111 1011  = Mн
= Mн
1.111111 1011 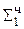
+ 0.000010 10 00  = -2Mн ∙ 22
= -2Mн ∙ 22
0.000010 0011 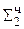
+ 1.110110 0000  = 2Mн ∙ 24
= 2Mн ∙ 24
1.111000 0011 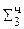
+ 0.1010 00 0000 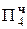 = -2Mн ∙ 26
= -2Mн ∙ 26
0.100000 0011 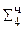 =Mн×Mт
=Mн×Mт
Матричные методы умножения
Кроме рассмотренных методов ускоренного умножения существуют методы умножения, основанные на использовании матриц промежуточных результатов.
Пусть имеем сомножители:
Мн = А = аn ... a2 a1