Интегрирование методом Монте-Карло
В самом общем случае методом Монте-Карло можно назвать любой способ решения некоторой задачи, в котором используются случайные числа.
Геометрический алгоритм Монте-Карло интегрирования
Предположим, необходимо взять интеграл от некоторой функции. Воспользуемся, геометрическим образом интеграла как площади под графиком этой функции.
Для определения площади под графиком функции можно использовать следующий стохастический алгоритм:
· ограничим функцию прямоугольником, площадь которого Sp можно легко вычислить;
· «набросаем» в этот прямоугольник, некоторое количество точек (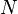
штук), координаты которых будем выбирать случайным образом;
· определим число точек (
штук), которые попадут под график функции;
· площадь области, ограниченной функцией и осями координат, даётся выражением:
.
При 
значение S, очевидно, будет стремиться к рассчитываемому интегралу.
Стохастический метод может оказаться наиболее предпочтительным в тех случаях, когда функция задана неявно, а область интегрирования задана в виде сложных неравенств. Представьте, например, что нужно численно оценить площадь внутри контура сложной формы, а никакого уравнения, описывающего этот контур нет. Зато можно отличить попадание точки со случайными координатами "внутрь" контура от попадания её "снаружи" – пусть даже по цвету пиксела на рисунке.
Рассмотрим пример реализации стохастического метода в системе MathCAD. Обратим внимание на то, как в прилагаемом документе осуществлен выбор прямоугольника для заполнения точками. Данный выбор основан на исследовании экстремальных значений функции в области интегрирования.
Программа в MathCAD
|
| - тестовая функция |
|
|
| - пределы интегрирования |
|
|
| Исследование функции на экстремумы |
|
|
|
|
|
| Значение координаты x в максимуме |
|
|
|
|
|
|
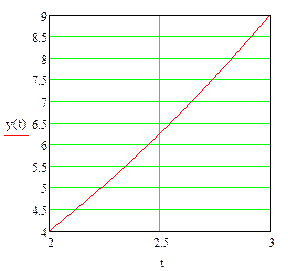
| Значение координаты x в минимуме |
|
|
|
| Реализация метода Монте-Карло |
|
| число испытаний |
|
| Значения координат случайных точек |
|
|
|
|
|
|
|
|
|
|
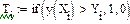
| Заполнение области точками |
|
Обычный алгоритм Монте-Карло интегрирования
Предположим, требуется вычислить определённый интеграл 
.
Рассмотрим случайную величину u, равномерно распределённую на отрезке интегрирования [ a, b ]. Тогда 
также будет случайной величиной, причём её математическое ожидание выражается как:
,
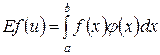где 
– плотность распределения случайной величины, равная 
на участке [ a, b ].
Таким образом, искомый интеграл выражается как:
.
Но математическое ожидание случайной величины можно легко оценить, смоделировав эту случайную величину и посчитав выборочное среднее.
Итак, бросаем на [ a, b ] N равномерно распределённых точек, и для каждой точки 
вычисляем 
. Затем вычисляем среднее:
.
В итоге получаем оценку интеграла: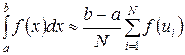 
.
Точность оценки зависит только от количества точек .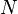
Этот метод имеет и геометрическую интерпретацию. Он очень похож на детерминистический метод (рис. под абзацем), с той разницей, что вместо равномерного разделения области интегрирования на маленькие интервалы и суммирования площадей получившихся «столбиков» мы забрасываем область интегрирования случайными точками, на каждой из которых строим такой же «столбик», определяя его ширину как 
, и суммируем их площади.
Ниже приведен пример реализации алгоритма с помощью программного модуля MathCAD. Программные модули сочетают в себе обособленность (поэтому их легко отличить от остальных формул) и простоту смыслового восприятия. Это позволяет инженерам самостоятельно решать довольно сложные задачи, не обращаясь за помощью к программистам. Сначала приведем модуль, а потом дадим комментарий.
Программа в MathCAD
|
|
|
|
|
| Проверка расчета |
Для вставки программного кода в документы в MathCAD имеется специальная панель инструментов Programming, которую можно вызвать на экран по цепочке View – Toolbars – Programming.
Большинство кнопок этой панели выполнено в виде текстового представления операторов программирования, поэтому их смысл понятен.
Нажмите кнопку Add Line (Добавить линию). Если приблизительно известно, сколько строк кода будет содержать программа, можно заранее создать нужное количество линий повторным нажатием кнопки Add Line (в нашем расчете будет 5 линий). Вставить строку можно этой же кнопкой, предварительно сместив курсор в крайнее левое (правое) положение и при необходимости нажав клавишу пробел.
Стрелка 
присваивает значение локальной переменной (т.е. переменной, используемой только внутри программы). Функция 
создает вектор из N случайных чисел ui, равномерно распределенных на отрезке [ a, b ].
Цикл for. За ключевым словом for следует переменная-счетчик, а после символа принадлежности вводится промежуток изменения этой переменной. Внутренние операторы цикла сдвинуты немного вправо. В нашем примере эти операторы оформлены в самостоятельную программу (хотя и не обязательно делать именно так). Новая вертикальная черта с двумя линиями выделяет программу, реализуемую циклом и представляющую собой расчет суммы, аппроксимирующей интеграл. Итогом завершения цикла и программы в целом будет значение этой суммы.
Задания для самостоятельного выполнения
1. Вычислите обоими методами интеграл
.
2. "Геометрическим" методом вычислите площадь между графиками зависимостей
и 
.
Постройте графики 
и заполните точками выбранный прямоугольник. Разделите цветом точки, попавшие внутрь искомой площади и за её пределы.
|
Пример с N = 100000 точками.
Внутри искомой площади n = 5568 точек.