Организация начала урока и мотивация.
Подготовка к уроку: открыли тетрадь, записали число, тему урока.
(Обеспечение мотивации)
Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя.
Девизом к сегодняшнему уроку будут следующие слова:
- Что есть больше всего на свете? – Пространство.
- Что быстрее всего? – Ум.
- Что мудрее всего? – Время.
- Что приятнее всего? – Достичь желаемого.
Хочется, чтобы ты на сегодняшнем уроке достиг желаемого результата.
Актуализация опорных знаний
Какие функции ты уже знаешь?
Что является графиком линейной функции?
Что надо знать чтобы построить график линейной функции?
Изучение нового материала
Видео урок смотри по ссылке https://www.youtube.com/watch?v=CrQlH1yZBuw
Одной из наиболее распространенных и изученных функций является квадратичная функция у = ах² + bх + с, где х - независимая переменная; а, b и с- некоторые числа (причем а ≠ 0).
Например, перемещение х тела при движении с ускорением а описывается квадратичной функций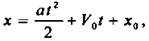 
где x0 и V0 - положение и скорость тела в начальный момент времени t = 0.
С частным случаем квадратичной функции у = х² (где а = 1, b = 0, с = 0) школьники уже знакомы. Графиком этой функции является парабола. Продолжим изучение квадратичных функций. Сначала ограничимся изучением функции у = ах².
Пример 1
Составим таблицу значений и в одной системе координат построим графики функций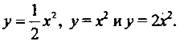 
| x | -2 | -1,5 | -1 | -0,5 | 0,5 | 1,5 | |||
| у = 1/2х2 | 1,12 | 0,5 | 0,12 | 0,12 | 0,5 | 1,12 | |||
| у = х2 | 2,25 | 0,25 | 0,25 | 2,25 | |||||
| y = 2х2 | 4,5 | 0,5 | 0,5 | 4,5 |
Отметив на координатной плоскости точки, приведенные в таблице, построим графики данных функций. Видно, что при каждом значении х значения функции у = 1/2х² в два раза меньше значений функции у = х², а значения функции у = 2х² в два раза больше значений функции у = х². Другими словами, график функции у = 1/2х² можно получить сжатием в два раза вдоль оси ординат графика функции у = х². График функции у = 2х2 можно получить растяжением в два раза вдоль оси ординат графика функции у = х².
|
|
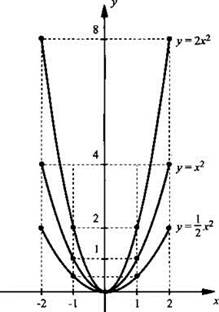
Вообще говоря, график функции у = ах² можно получить из параболы у = х² растяжением вдоль оси ординат в а раз при а > 1 и сжатием вдоль оси ординат в 1/a раз при 0 < а < 1. График функции у = ах² так же, как и график функции у = х², называют параболой.
Приведем свойства функции у = ах² при а > 0:
1. Область определения функции - промежуток (-∞; ∞).
2. Если х = 0, то у = 0. Следовательно, график проходит через начало координат.
3. Если х ≠ 0, то у > 0. Поэтому график расположен в верхней полуплоскости.
4. Функция четная, т. е. противоположным значениям аргумента соответствуют равные значения функции у(-х) = у(х). График функции симметричен относительно оси ординат.
5. Функция убывает в промежутке (-∞; 0] и возрастает в промежутке [0; ∞).
6. Функция ограничена снизу, у ≥ 0. Наименьшее значение у = 0 функция принимает при х = 0, наибольшего значения функция не имеет.
7. Область значений функции - промежуток [0; +∞).
Обсудим теперь свойства и график квадратичной функции у = ах2 при a < 0.
Пример 2
Составим таблицу значений и в одной системе координат построим графики функций у = 1/2х² и у = -1/2х².
|
|
| x | -2 | -1,5 | -1 | -0,5 | 0,5 | 1,5 | |||
| у = 1/2х2 | 1,12 | 0,5 | 0,12 | 0,12 | 0,5 | 1,12 | |||
| у = -1/2х2 | -2 | -1,12 | -0,5 | -0,12 | -0,12 | -0,5 | -1,12 | -2 |
Отметим точки, приведенные в таблице, и построим графики данных функций. Видно, что при каждом значении х значения функции у = -1/2х² противоположны по знаку значениям функции у = 1/2х². Поэтому график функции у = -1/2х² получается из графика функции у = 1/2х² с помощью симметрии относительно оси абсцисс.
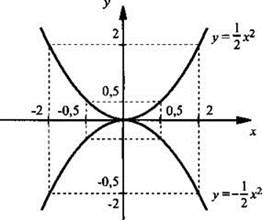
Теперь легко сформулировать свойства функции у = ах² при а < 0:
1. Область определения функции - промежуток (-∞; ∞).
2. Если х = 0, то у = 0. Следовательно, график проходит через начало координат.
3. Если х ≠ 0, то у < 0. Поэтому график расположен в нижней полуплоскости.
4. Функция четная, у(-х) = y(x). График функции симметричен относительно оси ординат.
5. Функция возрастает в промежутке (-∞; 0] и убывает в промежутке [0; ∞).
6. Функция ограничена сверху, у ≤ 0. Наибольшее значение у = 0 функция принимает при х = 0, наименьшего значения функция не имеет.
7. Область значений функции - промежуток (-∞; 0].
Закрепление изученного материала.
Русский писатель Лев Николаевич Толстой сказал: «Знание – орудие, а не цель». Давайте учиться использовать полученные сегодня знания как орудие для выполнения заданий различного характера.
Работа по учебнику - № 91.
Выполняя упражнение, учащийся должен опираться на свойства функции и графика.
Итог урока
1. Какая функция называется квадратичной?
2. Как называют график квадратичной функции?
|
|
3. Приведите основные свойства и график функции у = ах² при а > 0.
4. Приведите основные свойства и график функции у = ах² при а < 0.
5. Как из графика функции у = x² получить график функции
у = ах² при а > 0.
Д\З Выучить п. 5, прочитать п. 6 решить № 93
ВНИМАНИЕ!!!
Проработать материал и выполнить задания ты должен 1 ноября 2021 года. Задания выполняешь в рабочей тетради. Выполненную домашнюю работу фотографируешь (вертикально) и пересылаешь мне
в vk https://vk.com/id589665126 до 20.00 1 ноября 2021 года
ЖЕЛАЮ УДАЧИ!