МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ФОРМЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
Базовые понятия
Математические модели в форме передаточных функций получили наибольшее применение для описания физических процессов в линейных стационарных динамических системах. Передаточные функции - динамические модели.
Базовым понятием в теории передаточных функций является преобразование Лапласа:
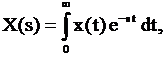(3.1)
которое устанавливает соответствие между функцией x(t) – вещественной переменной t и функцией X(s) – комплексной переменной s:
s = σ + jω, (3.2)
где x(t) – оригинал; X(s) – изображение (изображение по Лапласу).
Это соответствие обозначается так:
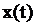
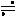X(s) (3.3)
или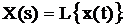 
(3.4)
Основные свойства преобразования Лапласа:
1) линейность:
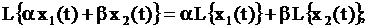(3.5)
2) дифференцирование:
при нулевых начальных условиях –
x(0) = x′(0) = x″(0) = … = x(n-1) (0) = 0 (3.6)
справедливо:
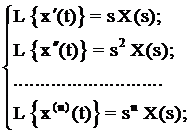(3.7)
3) интегрирование:
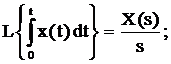(3.8)
4) теорема запаздывания:
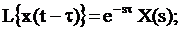(3.9)
5) теорема о свертке:
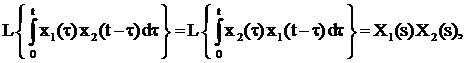(3.10)
где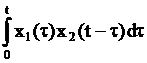 
, 
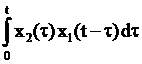– свертка функций x1(t) и x2(t) (интеграл свертывания).
Передаточная функция в форме изображений Лапласа
Пусть физическая система (см. рис. 3.1) описывается математической моделью в форме линейного дифференциального уравнения
a2y″(t)+a1y′(t)+a0y(t) = b1x′(t)+b0x(t) (3.11)
при нулевых начальных условиях:
y(0) = y′(0) = 0.
Применим преобразование Лапласа:
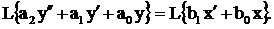(3.12)
Используя свойства линейности и дифференцирования оригинала, получим:
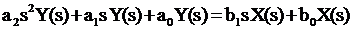(3.13)
или
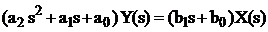. (3.14)
Выразим отношение изображения выходной величины Y(s) системы к изображению входной величины X(s):
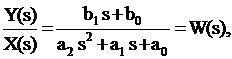(3.15)
где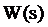 
– передаточная функция системы в форме изображений Лапласа.
Рассмотрим физическую систему с двумя входами (рис. 3.1).
Если физическая система имеет несколько входов, то она может быть описана несколькими передаточными функциями по каждому входу.
|
|
При определении передаточной функции относительно одной из входных величин остальные входные величины полагаются равными нулю.
Пусть физическая система описывается математической моделью вида:
a3y′′′(t)+a1y′(t)+a0y(t)= b2x′′(t)+b0x(t)+c0f(t) (3.16)
при нулевых начальных условиях.
Перейдем к изображениям Лапласа:
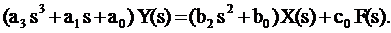(3.17)
Положим F(s) = 0, тогда передаточная функция относительно входа x(t)
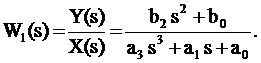(3.18)
Положим X(s) = 0, тогда передаточная функция относительно входа f(t)
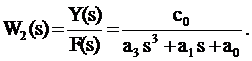(3.19)
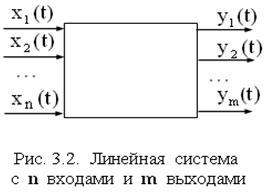
Для линейной физической системы с несколькими входами и выходами (рис. 3.2) передаточная функция превращается в матричную передаточную функцию:
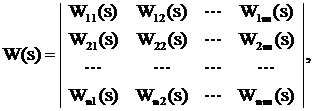(3.20)
где
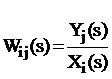– (3.21)
передаточная функция между i-м входом и j-м выходом.
Передаточная функция
В операторной форме
Передаточная функция в операторной форме получается формальным путем из дифференциального уравнения.
Пусть физическая система описывается линейной математической моделью вида:
a2y′′(t) + a1y′(t) + a0y(t) = b1x′(t) + b0x(t). (3.22)
Введем оператор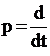 
, обозначающий операцию дифференцирования. Сделаем подстановку его в дифференциальное уравнение (3.21):
a2p2y(t) + a1py(t) + a0y(t) = b1px(t) + b0x(t) (3.23)
или
(a2p2 + a1p + a0)y(t) = (b1p + b0)x(t). (3.24)
Введем понятие операторов:
A(p)=a2p2+a1p+a0, (3.25)
B(p)=b1p+b0. (3.26)
Сделаем подстановку выражений (3.24) и (3.25) в уравнение (3.23):
A(p)y(t)=B(p)x(t) – (3.27)
это запись дифференциального уравнения (3.21) в операторной форме.
Передаточная функция в операторной форме
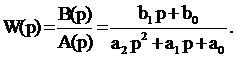(3.28)
Тогда дифференциальное уравнение (3.21) можно записать в виде:
y(t) = W(p)x(t). (3.29)
Передаточные функции W(s) и W(p) могут служить достоверным математическим описанием физической системы только при нулевых начальных условиях.
|
|
Для стационарных систем передаточные функции в форме изображения Лапласа W(s) и в операторной форме W(p) совпадают. На этом основании при рассмотрении линейных стационарных систем будем оперировать обобщенным термином «передаточная функция W(p)», полагая, что p – комплексная переменная.
Значение переменной p, при котором функция W(p) обращается в нуль, называется нулем передаточной функции. Значение p, при котором функция W(p) обращается в бесконечность, называется полюсом передаточной функции.
Если приравнять к нулю полином числителя передаточной функции W(p):
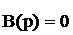, (3.30)
то корни уравнения (3.30) будут являться нулями W(p).
Если приравнять к нулю полином знаменателя передаточной функции системы W(p):
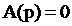, (3.31)
то корни уравнения (3.31) будут являться п олюсами W(p).
По расположению нулей и полюсов на комплексной плоскости делают вывод о свойствах исследуемой системы (качестве переходного процесса, устойчивости и др.)
Передаточная функция является самой компактной математической моделью, описывающей динамические свойства системы, и дает исчерпывающую характеристику взаимосвязи – «вход – выход».
Элементарные типовые звенья физических систем
Исследуемая физическая система может быть представлена в виде совокупности элементарных типовых звеньев. Этот прием лежит в основе разработки и анализа устройств и систем управления.
Элементарные типовые звенья могут рассматриваться в качестве моделей реальных функциональных элементов различной физической природы, разных принципов действия и конструктивного выполнения, но имеющих сходное математическое описание взаимосвязи «вход –выход».
|
|
Рассмотрим некоторые элементарные типовые звенья.
Пропорциональное (усилительное) звено. Передаточная функция W(p) = k.
Уравнение, связывающее мгновенные значения входной и выходной величин: y(t) = kx(t).
Реакция звена y(t) на единичное ступенчатое воздействие x(t) показана на рис. 3.3.
 |
Примеры функциональных элементов, моделируемых пропорциональным (усилительным) звеном: электронный усилитель, работающий на линейном участке характеристики в режиме малого сигнала (рис. 3.4), редуктор (рис. 3.5).
Инерционное (апериодическое) звено. Передаточная функция:
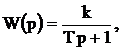
где k – передаточный коэффициент;
 |
Т – постоянная времени, характеризующая инерционные свойства звена.
Реакция инерционного (апериодического) звена на единичное ступенчатое воздействие показана на рис. 3.6.
Примеры функциональных элементов, моделируемых инерционным (апериодическим) звеном: электрический пассивный четырехполюсник (рис. 3.7), электрическая цепь (рис. 3.8), электрический генератор постоянного тока (рис. 3.9).