Понятие производной и её механический смысл.

Практическая работа №1

«Основы дифференциального исчисления.

Нахождение производных функций. Графики функций»

 

Цель занятия: Научиться решать примеры и задачи по данной теме

 

Вопросы теории (исходный уровень)

Введение. Содержание предмета. Инструктаж по технике безопасности.

1. Производная функции. Её физический и геометри­ческий смысл. (таблица производных основных элементарных функций)

2. Описание скорости протекания биологических процессов с помощью производной.

3. Градиенты.

4. Производные высших порядков.

5. Частные производные.

(самостоятельная подготовка)

 

Содержание занятия:

1. Ответить на вопросы по теме занятия

2. Решить примеры

 

Примеры

 

Найти производные следующих функций:

1)	2)	3)
4)	5)	6)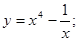
7) y = xa+b;	8)	9)
10) y = (1 – 3x2)(1 – x)3;	11) y = (2x – 1)(x2 – 1);	12) y = (1 – 4x3)(1 + 2x2);
13)	14)	15)
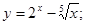
16)	17)	18) y = tg x – ctg x;
19) y = x – sin x;	20) y = loga x + ax;	21)
22) y = ex cos x;	23) y = sin x ln x;	24) y = sin x cos x;
25) y = x ln x;	26)	27)
28) y = 3 tg x ·ctg x;	29)	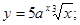30)
31)	32)	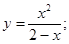33)
34)	35)	36)
37)	38)	39)
40)	41)	42)
43)	44)	45)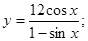
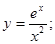
46)	47)	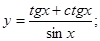48)
49)	50)	51) y = e3x;
52) y = cos 2x;	53) y = sin2 x;	54) y = sin x2;
55)	56) y = ln (x2 +1);	57)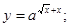
58) y = esin x;	59)	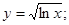60)
61) y = ln (ln x);	62)	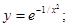63) y = sin(ln x);
64) y = ln (cos x);	65) y = (x2 – 3)5;	66)
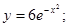
67)	68)	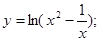69) y = ln (sin x + cos x);
70)	71)	72)
73)	74)	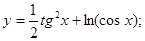75)
76) y = sin2 (3x2+2x + 4);	77)	78)
79)	80) y = x2 · 3x+1;	81) y = ln2 x · sin2x
82)	83)	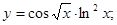84)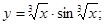
85) y = (x2 – 3)5 ln x;	86)	87)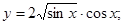
88)	89) y = ln x · tg x2;	90)
91) y = ln x2 · sin2x;	92)	93)
94) y = (1 – x2)3 cos x+ 2 sin2 x	95)	96)
97)	98)	99)
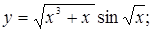
100)	101)	102)
103)	104)	105)
106)	107)	108)
109)	110)	111)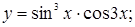
112)	113)	114)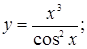
115)	116)	117)
118)	119)	120)
121)	122)	123)
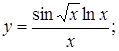
124)	125)	126)
127)	128)	129)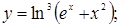
130)	131)	132)
133)	134)	135)
136)	137)	138)
139)	140)	141)
142)

 

Тема

Основные понятия высшей математики

 

Функция y = f(x) имеет пределом число А при стремлении х к а, если для каждого числа е>0 найдется такое число δ>0, что

| y— A|<е, при | х —a|<δ

lim y= А

| х —a|→0

Основные теоремы о пределах.

Предел постоянной величины

limА=А.

Предел суммы (разности) конечного числа функций

lim [f(x)+φ(x)+ψ(x)]= lim f(x)+ lim φ(x)+ lim ψ(x) x →а x →а x →а x →а

Предел произведений конечного числа функций

lim [f(x) • φ(x) • ψ(x)]= lim f(x) • lim φ(x) • lim ψ(x)

x →а x →а x →а x →а

Предел частного двух функций:

lim [f(x) / φ(x)]= lim f(x) / lim φ(x) при lim φ(x)≠0

x →а x →а x →а x →а

 

Производная.

 

Производной функции f(x)называется предел отношения прира-щения функции Δу к приращению аргумента Δх в точке хпри стремлении Δх к нулю:

 

ý=lim (Δy / Δx)

Δx →0

Производные некоторых функций:

у=С:	ý= 0;
y=x	ý=1
у = хμ:	ý=μxμ-1
у = аx: у = ех то	ý=axlna; ý= еx;
y=logax у = lпх	ý=(logae)/x=1/(x lna) ý=1/x
y=sinx y=cos x y = tgx. y = ctgx.	y'=cosx; ý = — sin x; ý =1/cos2x ý =-1/sin2x
y=arcsinx y=arccosx y=arctgx y=arcctgx	ý =1/(1-x2)1/2 ý =-1/(1-x2)1/2 ý =1/(1+x2) ý =-1/(1+x2)
y = v±u:	y' = u'±v'
y=uv	y' = u'v + v'u.
y=u/v:	y' =(u'v- v'u)/ v2
y = f1(u), если u = f2(x),	у'x = у'uu'x

 

 

 

ПОНЯТИЕ ПРОИЗВОДНОЙ И ЕЁ МЕХАНИЧЕСКИЙ СМЫСЛ.

Приращение аргумента и функции. Пусть функция у=f(x) определена на некотором интервале, х₀ и х – два произвольных значения аргумента из этого интервала. Разность между двумя значениями аргумента называется приращением аргумента: х – х₀ = Dх, откуда х = х₀ + Dх, то есть значение аргумента х можно определить через х₀ и его же приращение Dх.

Разность между двумя значениями функции называется приращением функции: Dу = Df = f(x₀ +Dx) – f(x₀).

Как видно из рис.1, приращение аргумента Dх изображается приращением абсциссы точки графика функции у = f(x), а приращение функции Df – приращение ординаты этой точки.

	Рис.1

Вычисление приращения любой функции у = f(x) удобно проводить по следующей схеме:

1) даем аргументу х приращение Dх и получаем точку х + Dх;

2) находим значение функции в точке х + Dх: f(x + Dx);

3) находим приращение функции: Df = f(x + Dx) – f(x).

Понятие непрерывности. Функция f(x) называется непрерывной в точке х₀, если:

1) функция определена в точке х₀ и в некоторой окрестности, содержащей эту точку;

2) предел приращения функции равен нулю при стремлении приращения аргумента к нулю, то есть

 

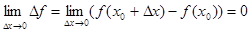
Определение производной. Задача нахождения скорости процессов привела к введению в математику понятия производной функции.

Пусть дана функция f(x), определенная на некотором интервале ] a, b [ и непрерывная на нем. Дадим аргументу приращение Dх, тогда функция получит приращение Df:

 

Отношение

является функцией от Dх и выражает среднюю скорость изменения функции f(x) относительно аргумента х на интервале ] х, х+Dх [.

Предел отношения Df/Dx приращения функции Df к приращению аргумента Dх, когда Dх стремится к нулю, при условии, что этот предел существует, называется производной функции f(x) в точке .

Таким образом, можно сделать следующий вывод: производная функции y = f(x):

В этом и состоит физический (в том числе механический) смысл производной.

Процесс нахождения производной называется дифференцированием, поэтому выражение «продифференцировать функцию» равносильно выражению «найти производную функции».