Опыты дэвиссона и джермера

В опытах Дэвиссона и Джермера изучалось рассеяние электронов, падающих на кристалл никеля. Схема их опытов изображена на рис. 1. Электронная пушка ускоряла и фокусировала электроны, испускаемые нитью накала, которые узким пучком падали в вакууме перпендикулярно определенной плоскости кристалла никеля. Детектор представлял собой коробку с двойными стенками. Между внутренней и внешней частями коробки поддерживалась регулируемая задерживающая разность потенциалов. Поэтому внутреннюю коробку достигали только те электроны, которые не испытывали потерь энергии. Они и давали вклад в измеряемый ток. Внешняя коробка, кристалл и последний электрод электронной пушки поддерживались при постоянном потенциале, так что при своем движении от пушки до кристалла и далее к детектору электроны находились по существу в нулевом электрическом поле. Детектор мог перемещаться. Это позволяло регистрировать электроны, отраженные кристаллом от 90° до 20°. Кристалл мог поворачиваться вокруг оси, совпадающей с направлением падающего пучка электронов.

В одной серии опытов Дэвиссона и Джермера измерялся ток, создаваемый рассеянными кристаллом электронами, в зависимости от ускоряющего напряжения 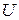и положения детектора . Кристалл был повернут вокруг вертикальной оси в положение, в котором сошлифованная поверхность кристалла покрыта правильными рядами атомов, перпендикулярными плоскости падения, расстояние между которыми 0,215 нм. Детектор перемещали в плоскости падения, меняя угол . При угле =50° и ускоряющем напряжении 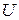= 54 В наблюдался резкий максимум интенсивности отраженных электронов, полярная диаграмма которого показана на рис.2.

Возникновение этого максимума можно объяснить только на основе волновых представлений, аналогичных дифракции пучка рентгеновских лучей с различным набором длин волн. В самом деле, рассмотрим волну, падающую нормально на плоскую дифракционную решетку, образованную атомами, расположенными в узлах кристаллической решетки (см. рис. 3) На рис.3 каждая жирная точка представляет собой проекцию цепочки атомов, расположенных на прямой, перпендикулярной плоскости рисунка. Падающая волна рассеивается каждым атомом, составляющим решетку. Если разность хода между двумя лучами, дифрагированными в направлении , равна

(8)

то в этом направлении должен наблюдаться дифракционный максимум. Тогда при заданном расстоянии между атомами из (8) можно вычислить длину волны. Если считать, что в данном случае наблюдается первый дифракционный максимум (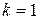), то длина волны равна

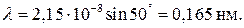
Соответствующая же длина волны де Бройля, вычисленная по формуле (6), равна 0,167 нм. Совпадение настолько хорошее, что полученный результат следует признать убедительным подтверждением гипотезы де Бройля. Тем более, что тот же опыт, повторенный с поликристаллической пластинкой из никеля, состоящей из множества мельчайших беспорядочно ориентированных кристалликов, не обнаружил никакого преимущественного направления при отражении электронов.

Другая серия опытов Дэвиссона и Джермера состояла в измерении интенсивности отраженного электронного пучка при заданном угле падения, но при различных значениях ускоряющего напряжения .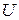

При этом теоретически должны появиться интерференционные максимумы отражения подобно отражению рентгеновских лучей от кристалла. От различных кристаллических плоскостей кристалла в результате дифракции падающего излучения на атомах исходят волны, как бы испытавшие зеркальное отражение от этих плоскостей. Данные волны при интерференции усиливают друг друга, если выполняется условие Брэгга-Вульфа:

(9)

где - межплоскостное расстояние, - угол скольжения.

Напомним вывод этой формулы. Из рис. 4 видно, что разность хода двух волн и , отразившихся зеркально от соседних атомных слоев, равна . Следовательно, направления возникновения интерференционных максимумов определяется условием (9).

Теперь подставляя в формулу (9) выражение (5) для дебройлевской длины волны, получим

(10)

т.е. значения , при которых образуются максимумы отражения, должны быть пропорциональны целым числам 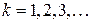, другими словами эти максимумы должны находиться на одинаковых расстояниях друг от друга.

Это и было проверено на опыте, результаты которого представлены на рис. 5. Видно, что максимумы интенсивности почти равноудалены друг от друга (такая же картина возникает и при дифракции рентгеновских лучей от кристаллов).

Различие теории и эксперимента в этом опыте заключалось в том, что положения дифракционных максимумов, наблюдаемых на эксперименте, не совпадали с положениями максимумов, определяемых из условия Брэгга-Вульфа (9) и показанных на рис.5 вертикальными стрелками. Особенно заметным это различие было для небольших значений, т.е. для небольшой величины ускоряющей разности потенциалов. Причина такого расхождения теории и эксперимента состоит в том, что условие Брэгга-Вульфа (9) не учитывает преломление электронных волн в металле.

ОПЫТ ТОМСОНА

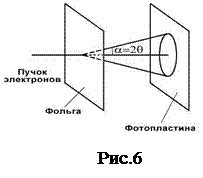В экспериментах Томсона наблюдалась дифракционная картина при прохождении монохроматического пучка быстрых электронов сквозь поликристаллическую фольгу толщиной см (рис. 6). Использование быстрых электронов объяснялось тем, что медленные электроны сильно поглощаются фольгой. На установленной за фольгой фотопластинке отчетливо наблюдались концентрические светлые и темные дифракционные кольца (рис. 7). Очень простым опытом Томсон доказал, дифракционная картина образовывалась именно рассеянными фольгой электронами, а не вторичными рентгеновскими лучами, испускаемыми атомами кристалла под действием электронного пучка. При создании магнитного поля в области между фольгой и фотопластинкой из-за отклонения электронов магнитным полем, вся дифракционная картина смещалась и искажалась. Этого, конечно, не должно было быть, при дифракции рентгеновских лучей.

Поясним, почему при рассеянии электронов на поликристаллическом образце на фотопластинке получаются концентрические дифракционные кольца. Поликристаллическая фольга, пронизываемая электронным лучом, состоит из большого числа очень маленьких ( см) монокристаллических зерен - кристаллитов, которые хаотически ориентированы по отношению друг к другу. На рис. 8 параллельными линиями показана ориентация некоторой выделенной системы атомных плоскостей в кристаллитах. Эта ориентация беспорядочно меняется при переходе от одного кристаллита к другому. При падении монохроматического пучка электронов на поликристалл в нем всегда найдутся кристаллиты, ориентированные так, что для отраженных от них электронов будет выполняться условие дифракционного максимума в соответствии с формулой Брэгга-Вульфа (9). Пусть пучок электронов падает под углом на систему атомных плоскостей кристаллита, представленную на рис. 9 параллельными линиями. Легко видеть, что дифрагировавший пучок электронов будет отклонен на угол по отношению к проходящему лучу. Таким образом, дифракция на отдельном кристаллите будет давать точку на фотопластинке.

3. Опыты по дифракции электронов проводил также Дж.П.Томсон (G.P.Thomson, 1927). Экспериментальный метод, использованный Томсоном, аналогичен известному методу Дебая-Шеррера (P.Debye, P.Sharrer,l9l6) в дифракции рентгеновских лучей. В этом методе вместо больших кри сталлов, необходимых для применения методов Лауэ и Брэг-га-Вульфа, используются поликристаллические пластинки. Если моноэнергетический пучок быстрых электронов падает на такую пластинку, то среди большого количества случайно ориентированных кристалликов пластинки всегда найдется такой микрокристалл, что для отраженного от него электрона будет выполняться условие дифракционного максимума в соответствии с формулой Брэгта-Вульфа. Дифрагированные лучи лежат на поверхности конуса (рис. 1.26). Его сечение на фотоплас­тинке регистрируется в виде концен­трических колец. Эта дифракционная картина называется дебаеграммой. Важнейшее условие проведения опыта состоит в том, чтобы осуществлялось однократное рассеяние электрона при прохождении его через пленку. Для этого толщина пленки должна быть доста­точно малой, порядка 10"⁵см. В случае более толстых пле­нок дифракционная картина сильно размывается из-за нало­жения различных отклонений. В эксперименте действитель­но наблюдались дифракционные кольца для электронного пучка при рассеянии пленками из разного материала. На рис.1.26,а изображена дебаеграмма, полу­ченная при дифракции электронов на поли­кристаллической пленке золота. Чтобы убе­диться, что дифракционная картина обус­ловлена именно электронами, а не рентге­новским излучением, возникающим при торможении электронов в веществе, на пути Рис 1 26.а дифрагированных электронов помещалось магнитное поле. Тогда вся картина дифракции сильно иска­жалась. В случае же дифракции рентгеновского излучения в этих условиях не должно происходить никаких изменений.

Из формулы (1.60) с помощью рис. 1,26 для малых уг­лов скольжения легко получить приближенное соотношение:

г L

— = п— = const, (1-64)

Я d

где г - радиус кольца на фотопластинке, L - расстояние от пленки до фотопластинки. Постоянство отношения (1.64) хорошо подтверждается в эксперименте.

В опытах Томсона использовались монохроматиче­ские пучки быстрых электронов (с энергией от 17,5 до 56,5 кэВ). Аналогичные опыты по дифракции электронов, но только с меньшими энергиями (до 1,7 кэВ), проводились П.С.Тартаковским.