СТАТИСТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ВОЛН ДЕ БРОЙЛЯ

 

Рассмотрим падающий на кристалл электрон. Соответствующая этому электрону волну де Бройля при прохождении через кристалл дифрагирует и порождает совокупность вторичных волн де Бройля. Вторичные волны интерферируют и согласно принципу Гюйгенса-Френеля должны давать на экране дифракционную картину, т.е. чередование максимумов и минимумов интенсивности волн де Бройля. Так как при регистрации электрон всегда ведет себя как целое и детектор, помещенный на экране в один из предполагаемых максимумов, регистрирует целый электрон, то нельзя допустить, что в каждом из максимумов находится какая-то доля электрона. Нельзя также допустить, что после прохождения через кристалл электрон попадает только в данный максимум. Это означало бы, что он проходит через кристалл, как классическая частица, а это несовместимо с явлением дифракции. При повторении опыта электрон обнаруживается также в одном из максимумов, но, вообще говоря, не в том же самом. Таким образом, мы пришли к противоречию между корпускулярными и волновыми свойствами частиц.

Это противоречие было разрешено М.Борном, который предложил статистическую (вероятностную) интерпретацию волн де Бройля, согласно которой волны де Бройля следует рассматривать как волны вероятности. Интенсивность волн де Бройля в каком-либо месте пространства пропорциональна вероятности обнаружить частицу в этом месте.

Дифракционная картина, возникающая в результате рассеяния пучка электронов на кристалле, объясняется следующим образом. Для каждого дифрагируемого электрона наиболее вероятно, что он полетит в направлении одного из максимумов интенсивности волн де Бройля. Соответственно, в направлении этих максимумов будет двигаться наибольшее число электронов. Вероятность того, что электрон полетит к одному из минимумов интенсивности волн де Бройля, равна нулю. Имеется также отличная от нуля вероятность, что электроны будут двигаться и в направлениях, не совпадающих с направлениями максимумов и минимумов интенсивности волн де Бройля.

ВОЛНОВАЯ ФУНКЦИЯ

 

Физическая теория, в которой описывается движение частиц, обладающих волновыми свойствами, первоначально получила название волновой механики. Однако, это название вскоре было заменено другим названием - квантовая механика - так как оказалось, что волновая механика предсказывает дискретный характер, то есть квантование различных физических величин у движущихся микрочастиц. Именно название квантовая механика закрепилось за этой теорией.

 

 

 

2. СООТНОШЕНИЕ НЕОПРЕДЕЛЫШОСТЕЙ

 

Из корпускулярно-волновсго дуализма следует, что микрочастицы существенно отличаются от? классических частиц. Понятие "длина волны в данной точке" лишено физического смысла, а поскольку импульс выражается через длину волны (см. (I),), то отсюда следует, что микрочастица с определенным импульсом имеет полностью неопределенную координату. И наоборот, если микрочастица находится в состоянии о точным значением координаты, то ее импульс неопределенен. Таким образом, микрочастица не может иметь одновременно и определенную координату (x, у, z) и определенную соответствующую проекцию импульса (Px, Py, Pz). Согласно соотношению неопределенностей Гейзенберга неопределенности в значениях этих величин удовлетворяют неравенствам

 

(4)

 

Отметим некоторые выводы, вытекащие из соотношения неопре­деленностей. Во-первых, состояние, в котором микрочастица находится в полном покое, невозможно. Во-вторых, для микрочастиц те­ряет смысл деление полной энергии на кинетическую и потенциальную: энергия должна определяться и измеряться лишь как полная энергия. В-третьих, для микрочастиц теряет смысл представление о движении частицы по траектории.

Наряду с соотношениями (4) имеет место неравенство

которое называется соотношением неопределенностей для энергии и времени

 

4. ВОЛНОВАЯ ФУНКЦИЯ

 

Известно, что плоская монохроматическая волна описывается уравнением

(5)

где .Обычно для упрощения вычислений переходят от (5) к комплекснозначащей функции

, (6)

действительная часть которой совпадает с выражением (5);

Выразив 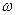и через Е и р, находим выражение для плоской волны де Бройля

, (7)

где . описывает свободную частицу, равномерно движущуюся с импульсом р в положительном направлении оси х.

Согласно статистической интерпретации вероятность обнаружить частицу в каком-либо месте пространства пропорциональна

,

т.е. равновероятно обнаружить частицу в любом маете пространства. Для равномерно движущейся свободной частицы этот результат очевиден. Он не получился бы, если вместо выражения (7) для волн де Бройля взять формулу (5). Таким образом, санкция VP принципиально комплексна.

При произвольных движениях частицы в произвольных силовых полях полное описание ее состояния дается не плоской волной де Бройля, а какой-то более слонной комплексной функцией . Она называется волновой функцией. пропорциональна вероятности. Вероятность достоверного события равняется единице. Достоверное событие состоит в том, что частица находится где-нибудь в пространстве, поэтому

(8)

При этом дает вероятность того, что частица находится в элементе объема dV, а есть плотность вероятности. Формула (8) называется условием нормировки.

Волновая функция удовлетворяет следующим стандартным условиям. Она должна быть:

• конечной (вероятность не может быть больше единицы);
• однозначной (вероятность не может быть неоднозначной величиной);
• непрерывной (вероятность не может изменяться скачком,.

Волновая функция удовлетворяет принципу суперпозиции: если и – волновые функции, описывающие какие-то два состояния частицы, то всякая их линейная комбинация с постоянными коэффициентами 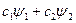представляет такие волновую функцию той же частицы, описывающую какое-то ее состояние.

 

5. УРАВНЕНИЕ ШРЕДИНГЕРА

 

Основная задача квантовой (волновой) механики состоит в нахождении волновых функций и связанных с ними физических следствий в самых разнообразных условиях. Для ее решения служит волновое уравнение или уравнение Шредингера.

Уравнение Шредингера имеет вид:

(9)

где m - масса частицы, - оператор Лапласа (), U – потенциальная энергия частицы в силовом поле, в котором она движется.

Нетрудно убедиться, что если U =0, то решением уравнения (8) является плоская волна де Бройля (7).

Особое значение в квантовой механике имеют стацио­нарные состояния. Это такие состояния, в которых все наблюдаемые физические величины не меняются в течение вре­мени. В стационарных состояниях

(10)

Например, плотность вероятности

от времени не зависит.

Подставляя (10) в (9), получаем уравнение для нахождения волновых функций и энергии стационарных состояний

Уравнение (II) называется уравнением Шредингера для стационарных состояний или стационарным уравнением Щредингера, а уравнение (9) - временным или нестационарным уравнением Шредингера.

Решения стационарного уравнения Шредингера, такие, что волновая функция и ее производные первого порядка удовлетворяют стандартным условиям конечности; однозначности и непрерывности, существуют, вообще говоря,.не при всяких значениях Е, а только при некоторых. Их называет собственными значениями энергии. Собст­венные значения энергии Е могут быть дискретными, а могут непрерывно заполнять конечный или бесконечный интервал. Соответственно говорят, что энергетический спектр дискретный.или непрерывный.

Если U при . а стандартные условия выполнены, то можно доказать справедливость следующих ре­зультатов.

1. При Е < 0 собственные значения энергии образуют дискретный спектр. Волновая функция стационарного состояния обращается в нуль на бесконечности. Согласно статистической интерпретации это значит, что вероятность найти частицу на бесконечности равна нулю, частица находится в практически ограниченной области пространства. Говорят, что частица находится в связанном состоянии.

2. Если Е > 0, то уравнение (II) имеет решения при любых положительных значениях Е. Положительные значения образуют непрерывный спектр. При в функция остается конечной, частица с отличной от нуля вероятностью может уходить в бесконечность. Говорят, что частица находится в несвязанном состоянии.

 

6. ЧАСТЩЛ В ОДНОМЕРНОЙ ПРЯМОЛХЖНОЙ "ПОТЕНЦИМШОЙ ЯМЕ" 0 БЕСКОНЕЧНО ВЫСОКИМИ "СТЕНКАМИ

 

"Потенциальной ямой" называется область пространства, в которой потенциальная энергия частицы U меньше некоторого значения Uo. Если потенциальная энергия частицы вне и внутри "потенциальной ямы" имеет следующие значения (рис. I)

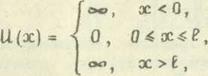
(12) то говорят, что частица находится в одномерной "потенциальной яме" бесконечно?!! глубины.

Для одномерного движения частица внутри "потенциальной ямы", где U = 0, стационарное уравнение Шредингера (II) имеет вид:

Общее решение этого уравнения есть

, (13)

где а и в - постоянные,

(14)

Вероятность найти частицу вне "потенциальной ямы" равна нулю. Это означает, что вне области (вне "ямы") .Чтобы волновая функция была непрерывна, на границах "ямы" (при х = 0 и х = l) она должна обращаться в нуль, т.е. должны выполняться условия.

(15)

Равенства (15) называются граничными условиями.

Из первого граничного условия,(15) для волновой функции (13) следует, что . Тогда

(16)

Второе граничное условие 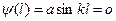выполняется только при

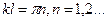(17)

Подставляя выражение (14) в условие (17), получаем

, n = 1, 2 … (18)

Таким образом, уравнение Шредингера, описывающее движение частицы в бесконечно глубокой "потенциальной яме", удовлетворяется только при собственных значениях. Еn, зависящих от целого числа n. Следовательно, в этом случае энергия En частицы не может быть произвольной, а принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Еn называются уровнями энергии, а число n, определяющее Еn,. называется квантовым числом. Итак, микрочастица в "потенциальной яме" с беско­нечно высокими "стенками"; может иметь только дискретный ряд зна­чений энергии Еn, или, как говорят, может находиться только на определенном энергетическом уровне Еn.

Постоянную a - в выражений (16) определим из условия нормировки (8), которое для данного случая с учетом (17) запишется в виде

В результате интегрирования получим .Таким образом, собственные функции будут иметь вид:

, n = 1, 2, 3 … (13)

Графики собственных функций (19), соответствующие уровням энергии (18) при n =1, 2 и 3, приведены на рис. 2а. На рис. 26 изображена плотность вероятности обнаружения частицы на различных расстояниях от "стенок ямы", равная 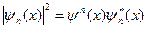для n = I, 2 и 3 Из рисунка следует, что, например, в квантовом со­стоянии с (1 = 2 частица не может находиться в середине "ямы", в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представле­ние о траекториях частицы в квантовой, механике не состоятельно.

Из формулы. (18) следует, что микрочастица в "потенциальной яме" с бесконечно высокими "стенками" не может иметь энергию

 

Рис. 2

 

остальные уровни

меньшую, чем минимальная энергия частица никогда не может опуститься на "дно ямы*. Этот результат следует из соотношения неопределенностей (4). Неопределенность координаты х частицы в "яме" шириной l равна 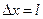. Тогда, согласно соотношению неопределенностей (4), импульс не может иметь точное, в данном случае нулевое значение. Неопределенность импульса . Такому разбросу значений импульса соответствует

кинетическая энергия

(n > I) имеют энергию, превышающую это минимальное значение.

Из выражения (18) вытекает также, что энергетический интер­вал между двумя соседними уровнями равен

(21)

При больших квантовых числах (n >>1) , т.е.

соседние уровни расположены близко друг к другу: тем ближе, чем больше П. Если Я очень велико,, то можно говорить о практически непрерывной последовательности уровней и характерная особенность квантовых процессов - дискретность - сглаживается. Этот результат является частным случаем принципа соответствия Бора, согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.

 

7. ТУНЕЛЬНЫЙ ЭФФЕКТ

 

Рассмотрим прямоугольный потенциальный барьер высотой Uо и шириной I. Пусть частица совершает одномерное движение вдоль оси X. Потенциальная энергия частицы U = U(х) изображена на рис. 3

.

(область I)

U= (область 2)

(область 3)

Рис. 3

В классической механике чйстица, обладая энергией Е > Uo, беспрепятственно пройдет над барьером, если же энергия частицы Е < И о, то частица никогда на пройдет через барьер, она отра­зится от него и будет двигаться в обратную сторону.

В квантовой механике даже при E-<U0 имеется отличная от ну­ля вероятность проникновения частицы через потенциальный барьер. Эффект.такого "просачивания" называется тунельным эффектом. Тунельный эффект - чисто квантовое явление, связанное с тем, что частицы обладают волновыми свойствами. Объяснить тунельный эффект можно основываясь на решении уравнений Шредингера, ко­торое для каждой из выделенных на рис. 3 областей имеет вид

 

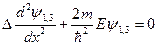(для области 1 и 3), (21)

(для области 2).

Общие решения дифференциальных уравнений;(21)

 

(для области 1) (22)

(для области 2) (23)

(для области 3) (24)

где ; . Первое слагаемое в (22) представляет плоскую волну, раопространящуюся в сторону барьера (падающую волну), второе - волну, отраженную от барьера. Коэффициент в (22) связан с интенсивностью пучка частиц, движущихся к барьеру. Положим . В области 3 есть только волна, прошедшая через барьер, поэтому коэффициент в 3 в формуле (24) следует принять равным нулю.

Таким образом, решения уравнения Шредингера для трех областей имеют вид:

(для области 1)

(для области 2) (25)

(для области 3)

Качественный вид функций (25) показан на рис. 3.

Из рис. 3 видно, что волновая функция отлична от нуля в области 3. Следовательно, частица тлеет отличную от нуля вероятность прохождения через потенциальный барьер конечной ширины.

Для описания туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, который определяется как отношение интенсивности прошедших через потенциальный барьерчастиц к интенсивности падающих частиц. D = .Для прямоугольного барьера

(26)

Туннельный эффект играет заметную роль, когда прозрачность барьера не очень мала. Это бывает в тех случаях, когда l соизмерима с атомными размерами. Так, при Uо-E= 10 эВ для электрона при l ~ 10^-10 м прозрачность D ≈ 0,37. Как следует из (26), D сильно зависит от массы частицы m, ширины барьера l и разности

Uo-E.

С классической точки зрения туннельный эффект представляется абсурдным, так как при Е<Ц должна быть отрицательной кинетическая энергия частицы. Однако туннельный эффект - явление чисто квантовое, не имеющее аналога в классической физике. Как отмечалось в. 2, в квантовой механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит соотношению неопределенностей. Действительно, если частица обладает определенной кинетической энергией, то это равнозначно тому, что она имеет определенный импульс. Аналогично, если частица имеет определенную потенциальную энергию Ц,, то это значит, что координата частицы точно задана. А так как координата и импульс частицы не могут иметь одновременно определенных значений, значит кинетическая и потенциальная энергии не могут быть точно определены. Поэтому ясно, что заключение об отрицательности кинетической энергии становится в данном случае беспочвенным.

 

8. ИСПОЛЬЗОВАНИЕ ЭЩ ДНЯ ИЗУЧЕНИЯ ТЕШ "ЭЛШШТЫКВАНТОВОЙ МЕХАНИКИ

 

Решение задач по данной теме содержит большой объем вычислительной работы. Облегчить ее позволяет использование ЭВМ. С этой целью разработан пакет программ, включающий алгоритмы расчета и моделирования следующих задач:

изучение волновых свойств частиц;

применение 'соотношения неопределенностей для оценки порядка физических величин микромира;

расчет волновых функций и моделирование поведения микрочастицы в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками";

4) моделирование процесса прохождения частицы через прямоугольный потенциальный барьер, расчеты коэффициента прозрачности барьера D и исследование зависимости D от ширины барьера, массы и энергии налетающей частицы.

После проработки теоретического материала предлагается, используя данный пакет программ, завершить изучение теш моделированием и расчетными упражнениями на ЭВМ. Задание на эту работу содержится в инструкции на рабочем месте.

Литература

Трофимова Т.И. Курс физики. -М.: Высшая школа, 1985,
§ 213-221.

Савельев И.В. itypc общей физики.-Т. 3. - М.: Наука,
1982, § 18-23, 26.

 

Волновые свойства частиц были обнаружены в экспериментах, типичных для световых волн: в дифракционных и интерференционных явлениях. Определим длину волны де Бройля электрона, прошедшего ускоряющую разность потенциалов 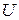. В этом случае его энергия равна 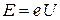, а импульс – , поэтому

или нм. (3)

В последнем выражении для значение 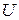берется в вольтах. Из формулы (3) видно, что электронам с энергиями порядка нескольких электронвольт соответствуют длины волн де Бройля порядка нескольких нанометров (порядка длин волн рентгеновских лучей). Поэтому для наблюдения дифракции электронов следует использовать кристаллические решетки, расстояние между узлами которых порядка нескольких нанометров.

Опыты по дифракции пучков электронов на кристаллах были проведены Дэвиссоном и Джермером, Томсоном и Тартаковским. В опытах Бибермана, Сушкина и Фабриканта было доказано, что не только электронные пучки, но и каждый отдельный электрон обладает волновыми свойствами. Описание этих экспериментов приведено в § 213 [l], в § IS [2].