Основные термодинамические процессы идеального газа

Контрольные задания

Методические указания

Контрольные задачи составлены по стовариантной системе, в которой к каждой задаче исходные данные выбираются из соответствующих таблиц по предпоследней и последней цифрам шифра (номера зачетной книжки) студента. Вариант работы должен соответствовать шифру студента. Работы, выполненные не по своему варианту, не рассматриваются.

Тетрадь для контрольной работы должна быть подписана следующим образом:

Тетрадь

Для контрольной работы

по курсу "Техническая термодинамика"

студента группы__________

факультета_______________

Ф.И.О.___________________

Шифр___________________

Вариант №_______________

При оформлении контрольных задач необходимо соблюдать следующие условия:

1. Выписывать условие задач и исходные данные.

2. Решение задач сопровождать кратким пояснительным текстом, в котором указывать, какие величины подставляются в формулу и откуда они берутся (из условия задачи, из справочника или были определены выше и т.д.).

3. Вычисления проводить в единицах СИ, показывать ход решения.

4. В конце работы привести список использованной литературы и поставить свою подпись.

5. Для письменных замечаний рецензента оставлять чистые поля в тетради и чистые 1-2 страницы в конце работы.

6. Исправления по замечаниям рецензента должны быть записаны отдельно на чистых листах в той же тетради после заголовка "Исправления по замечаниям".

 

Контрольная работа №1

Задача 1. Считая теплоемкость идеального газа зависящей от температуры, определить:

а) параметры газа в начальном и конечном состояниях;

б) изменение внутренней энергии;

г) изменение энтальпии;

в) теплоту, участвующую в процессе;

г) работу расширения.

Построить график процесса в координатах р-Т, p-v, v-T.

Исходные данные, необходимые для решения задачи, выбрать из таблицы 1.

Таблица 1

Предпоследняя цифра шифра	Процесс	t 1, °C	t 2, °C	Последняя цифра шифра	Газ	р, МПа	m, кг
	Изохорный				О2
	Изобарный				N2
	Адиабатный				H2
	Изохорный				N2
	Изобарный				СО
	Адиабатный				СО2
	Изохорный				N2
	Изобарный				H2
	Адиабатный				СО2
	Изобарный				СО

Зависимость теплоемкости от температуры дана в Приложении 1.

Задача 2. Для теоретического цикла ГТУ с подводом теплоты при постоянном давлении определить параметры рабочего тела (воздуха) в характерных точках цикла, подведенную и отведенную теплоту, работу и термический КПД цикла, если начальное давление р ₁ = 0,1 МПа, начальная температура t ₁ = 27°С, степень повышения давления в компрессоре b, температура газа перед турбиной t ₃.

Определить теоретическую мощность ГТУ при заданном расходе воздуха G. Дать схему и цикл установки в pv - и Ts -диаграммах. Данные для решения задачи выбрать из таблицы 3.

Таблица 3

Предпоследняя цифра шифра	b=	Последняя цифра шифра	t 3, °С	G, кг/с	Предпоследняя цифра шифра	b=	Последняя цифра шифра	t 3, °С	G, кг/с
	6,0					7,5
	6,5					7,0
	7,0					6,5
	7,5					6,0
	8,0					7,0

Указание: Теплоемкость воздуха принять не зависящей от температуры и равной 1,005 кДж/(кг×К).

 

Задача 3. Пар фреона-12 при температуре t ₁ поступает в компрессор, где адиабатно сжимается до давления, при котором его температура становится равной t ₂, а сухость пара х ₂ = 1. Из компрессора фреон поступает в конденсатор, где при постоянном давлении обращается в жидкость, после чего адиабатно расширяется в дросселе до температуры t ₄ = t ₁.

Определить холодильный коэффициент установки, массовый расход фреона, а также теоретическую мощность привода компрессора, если холодопроизводительность установки Q. Изобразите схему установки и ее цикл в Ts -диаграмме. Данные для решения задачи выбрать из таблицы 4.

Указание: Задачу решить с помощью таблиц параметров насыщенного пара фреона-12 (см.приложение 2).

Таблица 4

Предпоследняя цифра шифра	t 1, °С	t 2, °С	Последняя цифра шифра	Q, кВт	Предпоследняя цифра шифра	t 1, °С	t 2, °С	Последняя цифра шифра	Q, кВт
	-15					-20
	-10					-15
	-15					-10
	-20					-15
	-20					-20

 

ЛИТЕРАТУРА

1. Нащекин В.В. Техническая термодинамика и теплопередача. – М.: Высш. шк., 1980. – 470 с.

2. Кириллин В.А., Сычев В.В., Шейндлин А.Е. Техническая термодинамика. – М.: Энергоиздат, 1983. – 416 с.

3. Задачник по технической термодинамике и теории тепломассообмена / под ред. В.И.Крутова и Г.П.Петражицкого. – М.: Высш. шк., 1986. - 383 с.

 

Приложение 1

Средние изобарные мольныетеплоемкости mс _p некоторых газов

кДж/(кмоль×К)

t 1, °C	Воздух	О2	N2	H2	Водяной пар Н2О	СО	СО2
	29,073	29,274	29,115	28,617	33,499	29,123	35,860
	29,153	29,538	29,144	29,935	33,741	29,178	38,112
	29,299	29,931	29,228	29,073	34,188	29,303	40,059
	29,521	30,400	29,383	29,123	34,575	29,517	41,755
	29,789	30,878	29,601	29,186	35,090	29,789	43,250
	30,095	31,334	29,864	29,249	35,630	30,099	44,573
	30,405	31,761	30,149	29,316	36,195	30,426	45,758
	30,723	32,150	30,451	29,408	36,789	30,752	46,813
	31,028	32,502	30,748	29,517	37,392	31,070	47,763
	31,321	32,825	31,037	29,647	38,008	31,376	48,617
	31,598	33,118	31,313	29,789	38,619	31,665	49,392
	32,109	33,633	31,828	30,107	39,825	32,192	50,740
	32,565	34,076	32,293	30,467	40,976	32,653	51,858
	32,967	34,474	32,699	30,832	42,056	33,051	52,800
	33,319	34,834	33,055	31,192	43,070	33,402	53,604
	33,641	35,169	33,373	31,548	43,995	33,708	54,290
	33,296	35,483	33,658	31,891	44,853	33,980	54,881
	34,185	35,785	33,909	32,222	45,645	34,223	55,391

 

Приложение 2

Насыщенный пар фреона-12 (CCl₂F₂)

 

t, °C	P, МПа	v ¢, дм3/кг	v ¢¢, м3/кг	h ¢	h ¢¢	r	s ¢	s ¢¢
кДж/кг	кДж/(кг×К)
-20	0,1510	0,6868	0,11070	400,5	564,0	163,5	4,1183	4,7645
-15	0,1826	0,6940	0,09268	405,0	566,4	161,4	4,1356	4,7613
-10	0,2191	0,7018	0,07813	409,5	568,9	159,4	4,1528	4,7586
-5	0,2609	0,7092	0,06635	414,0	571,2	157,2	4,1698	4,7561
	0,3086	0,7173	0,05667	418,7	573,6	154,9	4,1868	4,7539
	0,3624	0,7257	0,04863	423,4	575,9	152,4	4,2036	4,7519
	0,4230	0,7342	0,04204	428,1	578,1	150,0	4,2204	4,7501
	0,4911	0,7435	0,03648	433,0	580,3	147,3	4,2371	4,7484
	0,5667	0,7524	0,03175	437,9	582,5	144,6	4,2537	4,7469
	0,6508	0,7628	0,02773	442,8	584,5	141,7	4,2702	4,7455
	0,7434	0,7734	0,02433	447,9	586,5	138,6	4,2868	4,7441
	0,8460	0,7849	0,02136	452,9	988,3	135,4	4,3031	4,7425
	0,9582	0,7668	0,01882	451,1	590,1	132,0	4,3194	4,7410

 

См. далее примеры решения задач!!!

Примеры решения задач

Задача 1. Считая теплоемкость идеального газа зависящей от температуры, определить: параметры газа в начальном и конечном состояниях, изменение внутренней энергии, теплоту, участвующую в процессе, и работу расширения, если процесс изобарный, рабочее тело – кислород, t ₁ = 1500°C, t ₂ = 100°C, р ₁ =12 МПа, m = 7 кг. Построить графики процесса в координатах в координатах p-v, p-Т и v-Т.

Решение.

1. Изобарный процесс – это процесс, протекающий при постоянном давлении, уравнение процесса р = const.

Параметры газа в начальном и конечном состояниях:

Т ₁ = 1500 + 273 = 1773 К;

Т ₂ = 100 + 273 = 373 К;

p ₁ = p ₂ =12×10⁶ Па;

Из уравнения состояния, записанного для начального и конечного состояний системы, определим v ₁ и v ₂:

p ₁ v ₁ = RT ₁,

p ₂ v ₂ = RT ₂,

где R – удельная газовая постоянная.

Для кислорода Дж/кг×К.

Так как p ₁ = p ₂, то .

Тогда м³/кг.

м³/кг.

2. Изменение внутренней энергии в изобарном процессе:

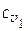, где и 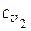- удельные теплоемкости газа при постоянном объеме при температурах Т ₁ и Т ₂ соответственно.

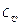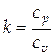В приложении 1 даны значения удельной молярной теплоемкости m в зависимости от температуры. Удельные теплоемкости газа при постоянном объеме и постоянном давлении связаны уравнением , где . Тогда .

Для двухатомных газов (например, кислород О₂) k =1,4. Определяя по таблице в приложении 1 значения m для температур Т ₁ и Т ₂, вычислим:

кДж/кг×К; кДж/кг×К;

кДж/кг×К; кДж/кг×К.

Тогда D u = 0,65×373 – 0,72×1773 = -1034,11 кДж/кг.

3. Изменение энтальпии

кДж/кг.

4. Теплота, участвующая в процессе,

кДж/кг.

Q = q×m = -1451,3 × 7 = -10159,1 кДж.

5. Изменение энтропии

кДж/кг×К.

6. Работа расширения

l = p (v ₂ – v ₁) = 12×10⁶(0,008-0,038)=-360000 Дж/кг = -0,36 МДж/кг.

L = l×m = -0,36×7 = 2,52 МДж.

7. График процесса

- в координатах pv: - в координатах pТ: - в координатах vТ:

Задача 2. Исходные параметры воздуха, поступающего в компрессор ГТУ с сжиганием топлива при р = const, р ₁ = 0,1 МПа, t ₁ = 20°С. Степень повышения давления в компрессоре ГТУ b = 6. Температура газов перед турбиной t ₃ = 700°С. Расход воздуха через компрессор G = 2×10⁵ кг/ч.

Определить:

- параметры всех точек идеального цикла ГТУ;

- теоретические мощности турбины, компрессора и всей ГТУ;

- параметры всех точек реального цикла (с учетом необратимости процессов расширения и сжатия в турбине и компрессоре), принимая внутренние относительные КПД турбины и компрессора соответственно ;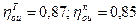

- внутренний КПД ГТУ, реальные мощности турбины, компрессора и всей ГТУ.

Представить оба цикла в Тs -диаграмме. Теплоемкость воздуха принять независимой от температуры и равной с_р = 1,005 кДж/кг×К.

По справочнику для воздуха k = 1,4.

Решение. Изобразим идеальный и реальный циклы ГТУ с изобарным подводом тепла и адиабатным сжатием воздуха в компрессоре в Тs -координатах.

1-2 – адиабатное сжатие воздуха в компрессоре;

2-3 – изобарный подвод тепла (горение топлива);

3-4 – адиабатное расширение продуктов сгорания в соплах

турбины;

4-1 – изобарный отвод тепла (выход продуктов сгорания в

атмосферу).

 

1-2-3-4-1 – обратимый цикл ГТУ (идеальный);

1-5-3-6-1 – необратимый цикл (реальный).

Температура в точках обратимого цикла:

1. Т ₁ = 20 + 273 = 293 К.

2. Так как процесс 1-2 адиабатный, то

).

3. Т₃ = 700 + 273 = 973 К.

4. Так как , то .

В данном цикле тепло подводится в изобарном процессе 2-3. Тогда

q ₁ = c _p(T ₃ – T ₂) = 1,005(973-489) = 486,42 кДж/кг.

 

Тепло отводится в изобарном процессе 4-1:

q ₂ = c _p(T ₄ – T ₁) = 1,005(583-293) = 291,45 кДж/кг.

 

Работа цикла

l _ц = q ₁ - q ₂ = 486,42 - 291,45 = 194,97 кДж/кг.

 

Термический КПД цикла в общем случае:

.

Теоретические мощности:

- турбины

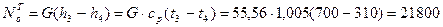кВт.

- компрессора

кВт.

- ГТУ в целом

кВт.

 

Температура в точках 5, 6 реального цикла рассчитываются таким образом. Из основной формулы для внутреннего относительного КПД компрессора:

найдем температуру в конце сжатия t ₅:

 

.

Для нахождения температуры в конце необратимого адиабатного расширения воспользуемся выражением для внутреннего относительного КПД турбины:

.

Тогда .

Внутренний КПД ГТУ:

.

Истинная мощность турбины

кВт.

Истинная мощность привода компрессора

кВт.

или 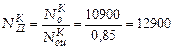кВт.

Истинная мощность ГТУ

кВт.

Вывод: приведеный расчет показывает, что истинная мощность ГТУ меньше теоретической в 1,8 раза вследствие необратимых процессов сжатия и расширения рабочего тела.

Задача 3. Пар фреона-12 при температуре t ₁ = -20°C поступает в компрессор, где изоэнтропно сжимается до давления, при котором его температура становится равной t ₂ = 25°C, а сухость пара х ₂ = 1. Из компрессора фреон поступает в конденсатор, где при постоянном давлении обращается в жидкость, после чего адиабатно расширяется в дросселе (т.е. при h = const) до температуры t ₄ = t ₁.

Определить: холодильный коэффициент установки; массовый расход фреона; теоретическую мощность привода компрессора, если холодопроизводительность установки Q = 150 кВт. Изобразите схему установки и ее цикл в.

Решение. Удельная холодопроизводительность

q ₂ = r ₁×(x ₁ – x ₂), кДж/кг,

где r ₁ – теплота парообразования при t ₁ (при t ₁ = -20°C из Приложения 2 найдем, что r ₁ = 163,5 кДж/кг);

x ₁, x ₂ – степень сухости пара перед компрессором и после дроссельного вентиля соответственно.

Степень сухости x ₁ пара определим по уравнению:

,

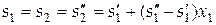где из приложения 2:

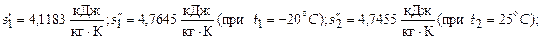
Следовательно .

Степень сухости после дроссельного вентиля определяем по уравнению:

,

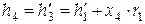где

.

Тогда .

Удельная холодопроизводительность .

Теплота, отведенная от рабочего тела в конденсаторе ,

где .

Тогда .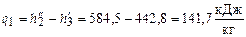

Работа, затраченная в цикле, l _ц = q ₁ – q ₂ = 141,7 – 116,4 = 25,3 кДж/кг.

Холодильный коэффициент .

Массовый расход фреона .

Теоретическая мощность привода компрессора .

Схема установки:

 

 

1 – дроссельный вентиль, 2- испаритель, 3 – компрессор, 4 – конденсатор.

 

Цикл в Т-s -координатах:

 

 

ТЕОРИЯ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ (!!!) + то, что есть в задачах

Основные термодинамические процессы идеального газа

Задачей исследования термодинамических процессов является нахождение следующих зависимостей и величин, характеризующих эти процессы:

1) уравнений, описывающих процесс в системах координат p - v, т.е. уравнений f (v, p) = 0, s-T, т.е. уравнений f ₁(s, p) = 0;

2) аналитической взаимосвязи между отдельными параметрами, характерной для рассматриваемого процесса, т.е. связи между параметрами p, v, T и s: p = f ₁(v), T = f ₂(v), T = f ₃(p), s = f ₄(T);

3) величины работы изменения объема рабочего тела;

4) величины изменения внутренней энергии;

5) величины работы изменения энтальпии рабочего тела;

6) величины работы изменения энтропии рабочего тела;

7) количества тепла, подведенного за время процесса к рабочему телу или отведенного от него;

8) величину теплоемкости рабочего тела.

В технической термодинамике изучаются следующие основные термодинамические процессы: изохорный, изобарный, изотермический, адиабатный и политропный.

Охарактеризуем по приведенной выше схеме каждый из перечисленных термодинамических процессов.

 

Изохорный процесс

Процесс, протекающий при постоянном объеме, называется изохорным. Кривая процесса называется изохорой.

1) Уравнение процесса v = const;

2) Связь параметров p ₁ v ₁ = RT ₁

р ₂ v ₂ = RT ₂

3) График процесса в координатах p - v (рис.5):

процесс 1-2 – подвод тепла; процесс 2-1 – отвод тепла.

Внешняя работа газа при v = const равна нулю, так как d v = 0.

Следовательно .

4) Изменение внутренней энергии из D u = с _v (Т₂ – Т₁).

5) Изменение энтальпии D h =с _p (Т₂ – Т₁).

6) Изменение энтропии ;

.

7) Количество теплоты d q = d u + d l.

Так как d l = 0, d q = d u; q = D u.

Изобарный процесс

Процесс, протекающий при постоянном давлении, называют изобарным. Кривая процесса называется изобарой.

1) Уравнение процесса р = const;

2) Связь параметров p ₁ v ₁ = RT ₁

р ₂ v ₂ = RT ₂

.

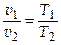3) График процесса в координатах p - v (рис.7):

процесс 1-2 – подвод тепла;

процесс 2-1 – отвод тепла.

Удельная работа газа при р = const выражается следующим уравнением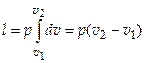

4) Изменение внутренней энергии D u = с _v (Т₂ – Т₁).

5) Изменение энтальпии D h =с _p (Т₂ – Т₁).

6) Изменение энтропии ;

.

7) Количество теплоты d q = d h – v d p. Так как d p = 0, d q = d h; q = D h.

 

Изотермический процесс

Процесс, протекающий при постоянной температуре, называют изотермическим (Т = const, d Т = 0). Кривая процесса называется изотермой.

1) Уравнение процесса Т = const; (p v = const)

2) Связь параметров p ₁ v ₁ = RT ₁

р ₂ v ₂ = RT ₂

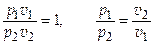(закон Бойля-Мариотта).

3) график процесса в координатах p - v (рис.9): процесс 1-2 – подвод тепла; процесс 2-1 – отвод тепла.

Удельная работа газа при Т = const выражается следующим уравнением ,

Но из уравнения изотермы имеем pv = p ₁ v ₁, или , поэтому

.

4) изменение внутренней энергии D u =0.

5) изменение энтальпии D h =0.

6) количество теплоты d q = d h + d l. q = l. Так как d p = 0, d q = d h; q = D h.

7) Изменение энтропии: .

Адиабатный процесс

Процесс, протекающий без подвода и отвода теплоты, т.е. при отсутствии теплообмена рабочего тела с окружающей средой, называют адиабатным, кривая этого процесса называется адиабатой.

1) Уравнение процесса .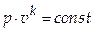

2) Связь параметров:

3) Адиабата в координатах pv (рис.11)идет круче изотермы, так как k >1.

4) изменение внутренней энергии .

5) изменение энтальпии .

6) Для обратимого адиабатного процесса количество теплоты d q = d u + d l = 0.

Работа совершается за счет убыли внутренней энергии: d l = - d u.

d l = - d u = - с_v (T ₂ – T ₁) = с_v (T ₁ – T ₂)

.

7) изменение энтропии 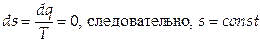.