Вариационные принципы. Стохастические модели.
Вариант 4
Задание 2.1. Пусть заданы координаты точек А и С. Точка В лежит на прямой y = 0. Используя вариационные принципы построения математических моделей, найти:
а) условие, при котором ломаная АВС имеет наименьшую длину;
б) числовое значение этого условия;
в) наименьшую длину ломаной АВС.
Дано:
А (-10;15)
С (20;10)
Решение:
Сделаем чертёж.
Длина ломаной АВС равна сумме длин отрезков АВ и ВС:
По теореме Пифагора из 
АА1В и СС1В:
Тогда длина ломаной АВС равна:
или
(1)
Подставив в уравнение (1) координаты точек А (-10;15) и С (20;10) и обозначив координаты точки В (x, 0), находим:
.
Получили зависимость длины ломаной от абсциссы точки B, т.е. функцию:
математическая модель.
а) Условие, при котором ломаная ABC имеет наименьшую длину:
Решая уравнение (1) в программе Maxima [2], получим:
б) Числовое значение x находим решением уравнения (1):
в) Наименьшая длина ломаной АВС:
Обозначим вторую производную через l 1 и вычислим её значение при х =8 в программе Maxima:
Так как при х =8 вторая производная l 1 больше нуля, l 1≈0,0437, то длина ломаной АВС будет наименьшей:
Ответ: а) 
, 
б) 
; в)
Теория к заданию 2.2.
Стохастические модели
Значительно более полные и объективные результаты можно получить при переходе от детерминированных к стохастическим моделям, то есть при переходе от точно заданных величин к соответствующим случайным величинам.
При этом константы (s, l, r, l,…) заменяются случайными величинами xs, xl, xr, x l,…, подчиненными определенным законам распределения.
Однократное исследование стохастической модели приведёт к некоторой случайной величине функции отклика x W, представляющей собой, вообще говоря, ограниченную ценность. Для получения значимых результатов необходимо провести многократное исследование модели и получить распределение результирующей характеристики в интересующем исследователя диапазоне. Поверхность отклика в этом случае представляет собой некий размытый слой переменной плотности.
Такой метод исследования стохастической модели получил название метода статистических испытаний или метода Монте-Карло.
Трудоёмкость исследования стохастических моделей существенно выше, чем моделей детерминированных:
1) Значительно возрастает объём исходной информации: замена констант случайными величинами, введение законов распределения этих величин усложняют модель.
2) Для получения распределения результирующей функции необходимо многократное исследование модели.
С другой стороны, полученное при статистическом моделировании распределение характеристик системы даёт чрезвычайно ценную информацию. Такое распределение позволяет оценить не только среднее значение изучаемой величины, но и разброс этих значений, вероятности появления тех или иных значений при конкретном испытании и их зависимость от различных факторов.
Очень часто используют нормальный или гауссовский закон распределения, для которого плотность вероятности f (x) и функция распределения R (х) задаются следующими соотношениями:
– вероятность того, что случайная величина попадет в интервал (х, x+dx):
;
– вероятность того, что случайная величина попадет в интервал (- ¥, х):
Наряду с нормальным законом, используются и другие законы распределения случайных величин. Плотность вероятности и функция распределения при равномерном распределении определяются по формулам:
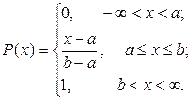
Выбор закона распределения для конкретной случайной величины, входящей в стохастическую модель, может быть обоснован экспериментально или теоретически.
При использовании метода статистических испытаний характеристики изучаемой системы оцениваются на основе некоторой ограниченной выборки реализаций. Поэтому важно определить достоверность этой оценки.
Можно показать, что эта ошибка удовлетворяет неравенству:
.
Здесь р – вероятность рассматриваемого состояния; a – вероятность невыполнения оценки (уровень риска). Доверительная вероятность р пребывания системы в некотором состоянии определяется частотой этого события при моделировании:
,
где n + – число реализаций, при которых наблюдалось изучаемое состояние системы; n – общее число реализаций.
Эта оценка является приближённой, так как определяется на основе ограниченной выборки. Отношение 
называется выборочной статистикой.
Ошибка моделирования определяется отклонением выборочной статистики от вероятности:
,
где вероятность выполнения этой оценки равна 1– a.
Погрешность стохастического моделирования обратно пропорциональна 
. То есть увеличение точности при стохастическом моделировании требует значительного увеличения числа реализаций. Для уменьшения погрешности в 10 раз необходимо увеличить число реализаций в 100 раз. Поэтому метод статистических испытаний не может дать решения с очень высокой степенью точности. Считается, что допустимая ошибка может составлять 1-5% максимальной величины, полученной при моделировании.
Величина ошибки зависит также от вероятности р оцениваемого состояния и допустимого уровня риска a. Обычно a задают на одном из фиксированных уровней: 0,005; 0,01; 0,025; 0,05; 0,1.
Эмпирические математические модели
Переход к эмпирическим моделям предполагает заведомый отказ от аналитических методов исследования. Поэтому эмпирические модели более разнообразны и включают в себя различные по форме математические зависимости.
При разработке эмпирической математической модели предполагается использование экспериментальных данных, полученных при испытаниях объектов. Результаты таких испытаний всегда представляют собой наборы величин, характеризующих работу объекта или системы при различных сочетаниях управляющих параметров.
Наиболее эффективным средством представления результатов экспериментов в системах математического моделирования являются эмпирические модели.
При построении эмпирической модели обычно предполагается, что физическая теория работы объекта отсутствует или по тем или иным причинам не может быть использована.
Объект идентификации представляет собой так называемый «чёрный ящик» с некоторым числом регулируемых (или, по крайней мере, измеряемых) входов х и одним или несколькими наблюдаемыми (измеряемыми) выходами (Рис.2.1).
Здесь xi – управляющие переменные; w i – неопределенности (шумы); qi – ограничения; W – характеристическая функция.